2023.07.05 - [ML(머신러닝)/Time Series] - Transformer 기반 Time Series Forecast 논문 알아보기
2023.07.06 - [ML(머신러닝)/Time Series] - TimeSeries Forecast) Transformer보다 좋다는 LSTF-Linear 알아보기
2023.07.12 - [ML(머신러닝)/Time Series] - TimeSeries) PatchTST 논문과 코드 살펴보기
2023.10.13 - [분류 전체보기] - TimeSeries) TSMixer 논문 및 구현 살펴보기
Are Transformers Effective for Time Series Forecasting?
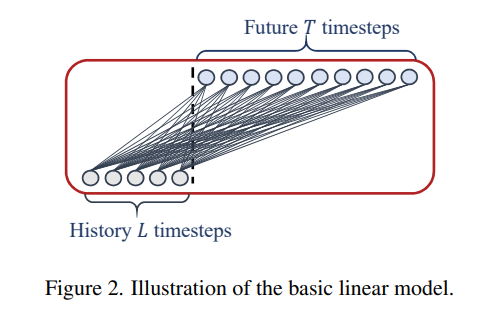
long-term time series forecasting (LTSF)에서 Transformer에 대해서 알아봤고, 이 논문은 그 이후에 Transformer는 이 논문에 적절하지 않고, 저자가 제안하는 방식으로 해도 충분히 성능이 나온다고 주장하였습니다.
굉장히 간단한 아이디어로 기존 Transformer보다 좋은 성능을 내었다고 합니다.
전반적인 구조는 다음과 같습니다.
최근에는 Transformer를 기반으로 한 장기 시계열 예측(LTSF) 솔루션들이 급증하고 있습니다.
그러나 이 연구에서는 Transformer 기반 방법의 타당성을 의심하며, 단순한 선형 모델인 LTSF-Linear이 기존의 Transformer 기반 모델보다 우수한 성능을 보인다는 결과를 제시합니다. 또한, LTSF 모델의 다양한 설계 요소가 시간적 관계 추출 능력에 미치는 영향을 연구하며, 이러한 발견이 LTSF 작업에 대한 새로운 연구 방향을 열어야 함을 주장합니다. 미래에는 다른 시계열 분석 작업에 대한 Transformer 기반 솔루션의 타당성을 다시 고려해야 할 것을 제안합니다.
논문에서는 Transformer가 positional encoding을 사용하여, 순서 정보를 일부 보전하고, sub-series를 포함하는 토큰을 임베딩하는 것은 일부 정렬 정보를 보존하는 데 도움이 됩니다. 그러나 순열 무관(permutation-invariant)(self-attention) 메커니즘의 본질로 인해 시간 정보의 손실은 불가피합니다.
Transformer의 주요 작동 원리는 멀티 헤드 셀프 어텐션 메커니즘에서 나오는데, 이는 긴 시퀀스 내 요소들 간의 의미론적 상관관계를 추출하는 능력을 가지고 있습니다.
그러나 시계열 데이터 분석에서는 순서 자체가 가장 중요한 역할을 하는데, 셀프 어텐션은 순서에 반감적인 특성(anti-order)을 가지고 있어 시간 정보의 손실이 발생할 수 있습니다. 따라서 Transformer가 장기 시계열 예측에 실제로 효과적인지에 대한 의문을 제기합니다.
예를 들어, 문장 내 일부 단어의 순서를 바꿔도 문장의 의미는 크게 유지됩니다.
그러나 시계열 데이터를 분석할 때는 숫자 데이터 자체에 의미가 부족하며, 연속적인 점들 사이의 시간적 변화를 모델링하는 데 주로 관심이 있습니다. 즉, 순서 자체가 가장 중요한 역할을 합니다.
저자들은 실험을 통해 교통, 에너지, 경제, 날씨 및 질병 예측 등 다양한 실제 응용 분야에서 Transformer보다 나은 성능을 얻을 수 있었고, 실제로 Transformer에서 그런 시간적 관계를 추출하지 못하는 것을 발견했다고 주장합니다.
기여한 점
- 우리의 지식으로는, 이 연구는 장기 시계열 예측 작업에 대한 Transformer의 효과성에 도전하는 첫 번째 연구입니다.
- 우리의 주장을 검증하기 위해, 우리는 LTSF-Linear라는 이름의 간단한 한 층 선형 모델 집합을 소개하고, 기존의 Transformer 기반 LTSF 솔루션과 비교합니다. LTSF-Linear은 LTSF 문제에 대한 새로운 기준점이 될 수 있습니다.
- 우리는 기존 Transformer 기반 솔루션의 다양한 측면에 대해 포괄적인 경험적 연구를 수행합니다. 이는 긴 입력을 모델링하는 능력, 시계열 순서에 대한 민감도, 위치 인코딩과 sub-series 임베딩의 영향, 그리고 효율성 비교 등을 포함합니다. 우리의 발견은 이 분야의 미래 연구에 도움이 될 것입니다.
시계열 예측(TSF)에 전제조건
IMS( Iterated multi-step) / DMS(direct multi-step)
시계열 예측 문제의 기본적인 형식과 다단계 예측 방법에 대해 설명하고 있습니다. 시계열 데이터는 여러 개의 변수(C variates)로 이루어져 있으며, 과거 데이터를 기반으로 미래 시간 단계에서의 값을 예측하는 작업입니다. T > 1인 경우, 다단계 예측을 위해 단일 단계 예측기를 학습하고 반복적으로 적용하는 IMS 예측 방법과, 한 번에 다단계 예측 목적을 최적화하는 DMS 예측 방법이 있습니다. IMS 예측은 DMS 예측보다 분산이 작지만 오류 누적 효과가 있을 수 있습니다. 따라서 IMS 예측은 단일 단계 예측기의 정확도가 높고 T가 작은 경우에 선호됩니다. 반면에 DMS 예측은 단일 단계 예측 모델을 편향되지 않게 얻기 어렵거나 T가 큰 경우에 더 정확한 예측을 제공합니다.
기존 변형된 Transformer TSF의 형태

Time Sereis decomposition
시계열 예측에서는 데이터 전처리로 평균이 0인 정규화를 일반적으로 사용합니다. Autoformer는 각 신경 블록 뒤에 계절성 및 추세 분해를 적용하여 원시 데이터를 더 예측 가능하게 만듭니다. FEDformer는 Autoformer의 분해 방법을 기반으로 추세 성분을 여러 커널 크기로 추출하고 이를 혼합하는 전문가 전략을 제안합니다.
Input embedding strategies
Transformer 아키텍처의 셀프 어텐션 레이어는 시계열의 위치 정보를 보존할 수 없습니다. 시계열의 지역적 위치 정보와 전역적인 시간 정보는 중요하며, SOTA Transformer 기반 방법은 고정된 위치 인코딩, 채널 프로젝션 임베딩, 학습 가능한 시간 임베딩 등 여러 임베딩 전략을 사용하여 시계열 입력의 시간적 문맥을 강화합니다. 또한, 시간 합성곱 레이어나 학습 가능한 타임스탬프와 같은 시간적 임베딩도 사용됩니다.
Self-attention schemes
Transformer는 셀프 어텐션 메커니즘을 사용하여 쌍으로 된 요소 간의 의미론적 의존성을 추출합니다.
최근 연구에서는 바닐라 Transformer의 시간 및 메모리 복잡성을 줄이기 위해 효율성을 위한 두 가지 전략을 제안합니다.
LogTrans와 Pyraformer는 셀프 어텐션 방식에 희소성 편향을 도입하고, Informer와 FEDformer는 셀프 어텐션 행렬의 저랭크 속성을 활용합니다.
Autoformer는 셀프 어텐션 레이어를 대체하기 위해 시계열에 대한 자기 상관 메커니즘을 설계합니다.
Decoders
바닐라 Transformer 디코더는 자기 회귀 방식으로 시퀀스를 출력하여 추론 속도가 느리고 오류 누적 효과가 있습니다. 특히 장기 예측의 경우에는 더욱 그렇습니다. Informer는 DMS 예측을 위해 생성적인 스타일의 디코더를 설계합니다. 다른 Transformer 변형 모델들도 유사한 DMS 전략을 사용합니다. 예를 들어, Pyraformer는 디코더로 시공간 축을 연결하는 완전 연결 레이어를 사용합니다. Autoformer는 추세-주기성 성분과 시계열에 대한 자기 상관 메커니즘에서 얻은 두 가지 분해된 특성을 합하여 최종 예측값을 얻습니다. FEDformer도 제안한 주파수 어텐션 블록과 분해 방식을 사용하여 최종 결과를 디코딩합니다.
Transformer 디코더는 자기 회귀 방식으로 시퀀스를 출력하며, 추론 속도가 느리고 오류 누적 효과가 있습니다. LTSF 작업에서는 순서가 가장 중요한 역할을 하며, 순열 불변성 셀프 어텐션 메커니즘의 특성으로 인해 시간적 정보 손실이 발생합니다. 따라서 Transformer 기반 LTSF 솔루션의 효과성을 재검토하고자 합니다.
즉, self attention 방식 자체에서 시간정 정보 손실이 발생하여, 의문을 제기한다고 합니다.
제안 하는 방법 DLinear , NLinear
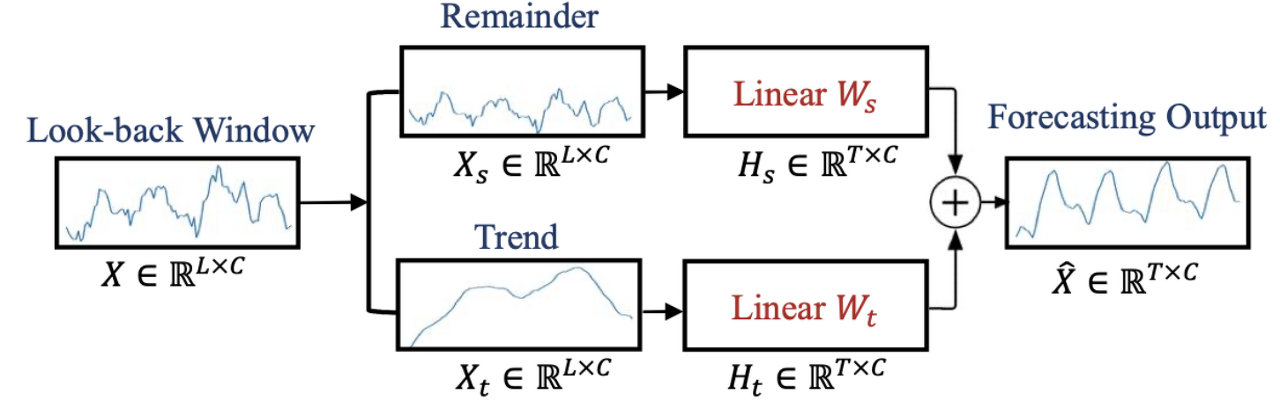
LTSF-Linear은 가장 간단한 DMS 모델로, 시간 선형 레이어를 사용하여 과거 시계열을 직접 회귀하여 미래 예측을 수행합니다. LTSF-Linear은 선형 모델의 집합이며, 다른 변수들 간에 가중치를 공유하고 공간적 상관관계를 모델링하지 않습니다. DLinear과 NLinear은 다양한 도메인의 시계열을 처리하기 위해 도입된 두 가지 전처리 방법입니다.
• DLinear은 Autoformer와 FEDformer에서 사용되는 분해 방식과 선형 레이어의 조합으로, 데이터에 명확한 추세가 있는 경우 바닐라 선형의 성능을 향상시킵니다.
즉, Autoformer/FEDformer에서 사용된 time series decomposition을 LTSF-Linear에 적용한 모델
• NLinear은 데이터셋에서 분포 시프트가 있는 경우 LTSF-Linear의 성능을 향상시키기 위해 사용되며, 입력 시퀀스를 간단하게 정규화하는 뺄셈과 덧셈 과정을 포함합니다.
즉, 마지막 시점의 값을 빼는 normalization을 LTSF-Linear에 적용한 모델
실험

실험은 논문을 참고하면 좋을 것 같습니다.
결국 이야기하고자 하는 것은 자기네 것이 좋다는 것이긴 해서 패스...
LSTF-Transformer에 대한 추가 분석 결과
하나하나 좋은 실험결과인 것 같아서 살펴보고자 합니다.
1. 기존의 LTSF-Transformer는 더 긴 입력 시퀀스에서 시간적 관계를 잘 추출할 수 있을까요?
시계열 예측의 정확성은 과거 데이터에서 얼마나 많은 것을 배울 수 있는지를 결정하는 look-back window의 크기에 크게 영향을 받습니다. 일반적으로 강력한 TSF 모델은 큰 look-back window 크기에서 더 좋은 결과를 얻을 수 있는 강력한 시간적 관계 추출 능력을 가져야 합니다.
저자들은 입력 look-back window 크기의 영향을 연구하기 위해 L ∈ {24, 48, 72, 96, 120, 144, 168, 192, 336, 504, 672, 720}로 실험을 진행했습니다 (장기 예측을 위한 T=720).
그림 4는 두 데이터셋에 대한 MSE 결과를 보여줍니다. 이전 연구 [27, 30]의 관찰과 마찬가지로, 기존의 Transformer 기반 모델의 성능은 look-back window 크기가 증가할수록 악화되거나 안정적입니다.
반면, 모든 LTSF-Linear 모델의 성능은 look-back window 크기가 증가함에 따라 크게 향상됩니다.
따라서, 기존의 솔루션은 더 긴 시퀀스가 주어진 경우 시간적 정보를 추출하는 대신 시간적 노이즈에 과적합되는 경향이 있으며, 입력 크기 96이 대부분의 Transformer에 적합합니다.

2. 장기 예측에는 어떤 것을 배울 수 있을까요?
단기 시계열 예측의 경우, look-back window 내의 시간적 동적인 요소가 예측 정확도에 큰 영향을 미칩니다.
그러나 장기 예측의 경우, 모델이 추세와 주기를 정확하게 포착할 수 있는지에 따라 달라집니다.
즉, 예측 시간이 멀어질수록 look-back window 자체의 영향은 줄어듭니다.
이 가설을 검증하기 위해 표 3에서 동일한 720개의 미래 시간 단계에 대한 예측 정확도를 두 가지 다른 look-back window 데이터로 비교합니다: (i). 원래 입력인 L=96 설정 (Close로 불림)과 (ii). 원래 96개의 시간 단계 이전인 L=96 설정 (Far로 불림). 실험 결과, SOTA Transformer 모델의 성능이 약간 감소하는 것을 확인할 수 있으며, 이는 이러한 모델들이 인접한 시계열 순서에서 유사한 시간적 정보만을 포착하고 있다는 것을 나타냅니다. 데이터셋의 본질적인 특성을 포착하는 데는 일반적으로 많은 수의 매개변수가 필요하지 않습니다. 즉, 하나의 매개변수가 주기성을 나타낼 수 있습니다. 매개변수를 너무 많이 사용하면 과적합이 발생할 수 있으며, 이것이 LTSF-Linear가 Transformer 기반 방법보다 더 좋은 성능을 내는 이유의 일부를 설명합니다.

3. LTSF에는 self-attention 기법이 효과적일까요?
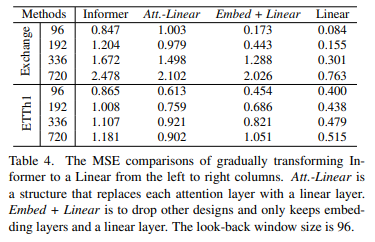
기존의 LTSF 벤치마크에는 self-attention 기법과 다른 복잡한 모듈들이 필요하지 않을 수 있다는 것을 알 수 있습니다. Informer 모델을 점진적으로 단순화한 결과, 성능이 향상되는 것으로 나타났습니다. 이는 self-attention 기법과 다른 복잡한 모듈들이 최소한 기존의 LTSF 벤치마크에는 필요하지 않다는 것을 시사합니다.
4. 기존의 LTSF-Transformer는 시간적인 순서를 잘 보존할 수 있을까요?
기존의 LTSF-Transformer는 시간적인 순서를 잘 보존하지 못하는 경향이 있습니다.
Transformer 기반 방법은 입력 시퀀스가 섞여도 성능에 큰 변화가 없지만, LTSF-Linear은 입력 시퀀스의 순서에 크게 영향을 받습니다. 이는 Transformer 기반 방법이 시간적 관계를 제한적으로 보존하며, 잡음이 많은 금융 데이터에서 과적합될 가능성이 있다는 것을 나타냅니다.
또한, 시간적 귀납적 편향이 있는 모델은 명확한 시간적 패턴이 있는 데이터에서 일부 시간적 정보를 추출할 수 있지만, 시간적 귀납적 편향이 없는 모델은 섞기 전략에 덜 영향을 받습니다. 전반적으로, 모든 경우에서 LTSF-Linear의 성능 하락이 Transformer 기반 방법보다 크며, 기존의 Transformer는 시간적인 순서를 잘 보존하지 못합니다.
표 5에서는 임베딩 전에 원시 입력을 섞어봅니다. 두 가지 섞기 전략을 사용합니다: Shuf.는 전체 입력 시퀀스를 무작위로 섞고, Half-Ex.는 입력 시퀀스의 첫 번째 절반과 두 번째 절반을 교환합니다.
결론적으로 봤을 때 특이한 점은 Transformer 기반의 방식에서는 성능이 흔들리지 않다는 것입니다.
즉 시간적인 방법론을 적용하지 않은 경우, permutation invariant한 특성으로 인해 성능이 떨어지지 않고, 즉 기존 시계열에 대한 정보를 잘 반영하지 못하고 있다는 점을 의미할 수 있습니다.

5. 기존의 LTSF-Transformer에 있어서 훈련 데이터의 크기는 제한적인 요소인가요?
기존의 LTSF-Transformer의 성능이 훈련 데이터의 크기가 작아서 나쁘다는 주장에 대해 논의되었습니다.
시계열 예측은 컴퓨터 비전이나 자연어 처리 작업과는 달리 수집된 시계열 데이터를 사용하기 때문에 훈련 데이터 크기를 확장하기가 어렵습니다. 하지만 실험 결과, 작은 훈련 데이터로 훈련된 모델이 더 낮은 예측 오류를 보여주는 경우가 많았습니다. 이는 작은 데이터셋이 더 명확한 시간적 특징을 유지할 수 있다는 것을 시사합니다. 따라서, Autoformer와 FEDformer의 성능에는 훈련 데이터 규모가 제한적인 이유가 되지 않는다는 것을 알 수 있습니다.
즉, 작은 데이터셋 안에서 시계열 정보가 충분히 다 있다면, 모델 성능에 크게 영향은 없다는 말입니다.
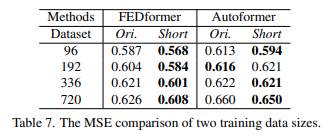
시계열 데이터는 결국 양보다는 질이 중요한 거고, 데이터 내에서 시계열 정보가 충분히 들어있다면, 소규모의 데이터로도 충분히 학습할 수 있다는 점을 시사하는 것 같습니다.
저자의 결론
이 연구는 Transformer 기반 솔루션들이 장기적인 시계열 예측 문제에 얼마나 효과적인지에 대한 의문을 제기합니다. 우리는 간단한 선형 모델인 LTSF-Linear을 사용하여 이를 검증하고, 놀라운 비교를 통해 왜 LTSF-Transformer가 이러한 연구들에서 주장하는 것만큼 효과적이지 않은지를 설명합니다. 이 연구는 향후 연구에 도움이 될 수 있기를 바라는 바입니다.
Future Work
LTSF-Linear은 모델 용량이 제한적이며, 강력한 해석 가능성을 가진 간단하면서도 경쟁력 있는 기준선 역할을 합니다.
예를 들어, 단일층 선형 신경망은 변화점으로 인해 발생하는 시간적 동적을 포착하기 어렵습니다. 따라서, 우리는 LTSF 문제에 대해 도전하기 위해 새로운 모델 디자인, 데이터 처리, 그리고 벤치마크에 대한 큰 잠재력이 있다고 믿습니다.
LSTF-LINEAR 기능
- O(1) 최대 신호 이동 경로 길이:
경로가 짧을수록 의존성을 더 잘 포착할 수 있으므로 [18], LTSF-Linear은 단기 및 장기적인 시간적 관계를 모두 포착할 수 있습니다. - 높은 효율성: LTSF-Linear은 최대 두 개의 선형 계층으로 구성된 선형 모델이므로 메모리 및 매개변수 비용이 훨씬 적게 들며 기존의 Transformer보다 더 빠른 추론 속도를 가집니다 (본 논문의 테이블 8 참조).
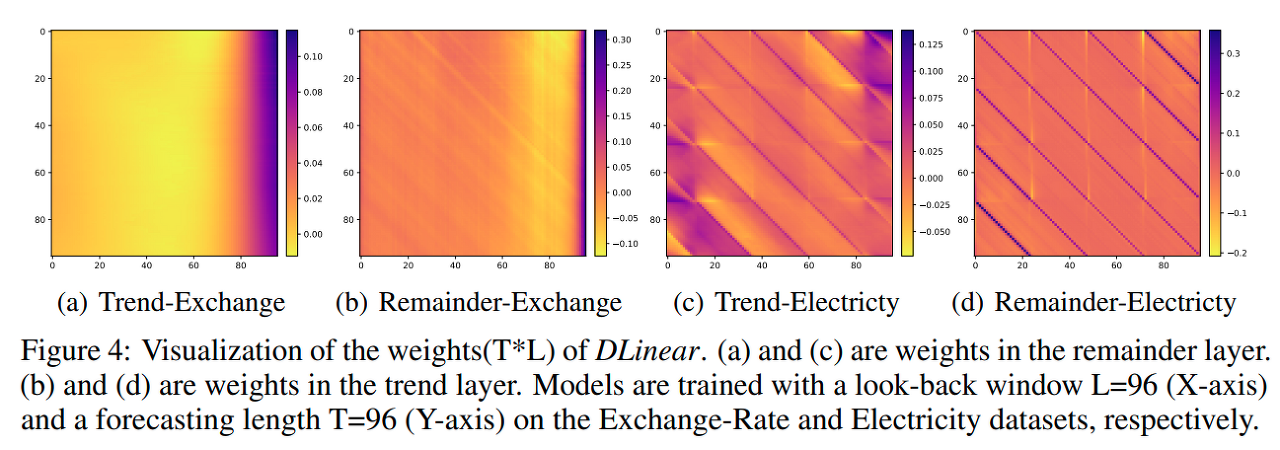
- 해석 가능성: 훈련 후, 계절성과 추세 분기에서 가중치를 시각화하여 예측 값에 대한 통찰력을 얻을 수 있습니다 [9].
- 사용 편의성: LTSF-Linear은 모델 하이퍼파라미터를 조정할 필요 없이 쉽게 얻을 수 있습니다.
LSTF-LINEAR 해석
이것을 보면, Trend를 학습하는 것을 알 수 있다.
코드 뜯어보기 (TODO)
Linear
class Model(nn.Module):
"""
Just one Linear layer
"""
def __init__(self, configs):
super(Model, self).__init__()
self.seq_len = configs.seq_len
self.pred_len = configs.pred_len
# Use this line if you want to visualize the weights
# self.Linear.weight = nn.Parameter((1/self.seq_len)*torch.ones([self.pred_len,self.seq_len]))
self.channels = configs.enc_in
self.individual = configs.individual
if self.individual:
self.Linear = nn.ModuleList()
for i in range(self.channels):
self.Linear.append(nn.Linear(self.seq_len,self.pred_len))
else:
self.Linear = nn.Linear(self.seq_len, self.pred_len)
def forward(self, x):
# x: [Batch, Input length, Channel]
if self.individual:
output = torch.zeros([x.size(0),self.pred_len,x.size(2)],dtype=x.dtype).to(x.device)
for i in range(self.channels):
output[:,:,i] = self.Linear[i](x[:,:,i])
x = output
else:
x = self.Linear(x.permute(0,2,1)).permute(0,2,1)
return x # [Batch, Output length, Channel]각각의 채널별로, pred_len 길이 만큼 한꺼번에 예측하는 코드이다. (DMS) 라고 보면 될 것 같다.
예시 코드 (한 채널만 예시로 해보는 코드 혹은 하나의 layer로 전체를 예측)
batch_size = 32
in_seq_len = 3
pred_len = 2
channel = 5
X = torch.randn(batch_size, in_seq_len, channel)
one_linear = nn.Linear(in_seq_len, pred_len)
output = torch.zeros(batch_size, pred_len, channel)
output[:,:,0]=one_linear(X[:,:,0])
output.size()
output[:,0,0]
output[:,1,0]
output = one_linear(X.permute(0,2,1)).permute(0,2,1)
output

NLinear
class Model(nn.Module):
"""
Normalization-Linear
"""
def __init__(self, configs):
super(Model, self).__init__()
self.seq_len = configs.seq_len
self.pred_len = configs.pred_len
# Use this line if you want to visualize the weights
# self.Linear.weight = nn.Parameter((1/self.seq_len)*torch.ones([self.pred_len,self.seq_len]))
self.channels = configs.enc_in
self.individual = configs.individual
if self.individual:
self.Linear = nn.ModuleList()
for i in range(self.channels):
self.Linear.append(nn.Linear(self.seq_len,self.pred_len))
else:
self.Linear = nn.Linear(self.seq_len, self.pred_len)
def forward(self, x):
# x: [Batch, Input length, Channel]
seq_last = x[:,-1:,:].detach()
x = x - seq_last
if self.individual:
output = torch.zeros([x.size(0),self.pred_len,x.size(2)],dtype=x.dtype).to(x.device)
for i in range(self.channels):
output[:,:,i] = self.Linear[i](x[:,:,i])
x = output
else:
x = self.Linear(x.permute(0,2,1)).permute(0,2,1)
x = x + seq_last
return x # [Batch, Output length, Channel]
모델이 결국 학습하는 부분은 변화량 부분만 학습하길 기대하는 것으로 보임.
마지막값 기준으로 얼마나 변화할 지를 예측하는데만 집중하게 만든 코드 같아 보임.
seq_last = X[:,-1:,:]
X2 = X - seq_last
one_linear = nn.Linear(in_seq_len, pred_len)
output = torch.zeros(batch_size, pred_len, channel)
output[:,:,0]=one_linear(X[:,:,0])
X2 = X2 + seq_last
output.size()
output[:,0,0] , output[:,1,0]
DLinear
class moving_avg(nn.Module):
"""
Moving average block to highlight the trend of time series
"""
def __init__(self, kernel_size, stride):
super(moving_avg, self).__init__()
self.kernel_size = kernel_size
self.avg = nn.AvgPool1d(kernel_size=kernel_size, stride=stride, padding=0)
def forward(self, x):
# [BATCH SIZE, SEQ_LEN, CHANNEL]
# padding on the both ends of time series
front = x[:, 0:1, :].repeat(1, (self.kernel_size - 1) // 2, 1)
end = x[:, -1:, :].repeat(1, (self.kernel_size - 1) // 2, 1)
x = torch.cat([front, x, end], dim=1)
x = self.avg(x.permute(0, 2, 1))
x = x.permute(0, 2, 1)
return x # [BATCH SIZE, SEQ_LEN, CHANNEL]
class series_decomp(nn.Module):
"""
Series decomposition block
"""
def __init__(self, kernel_size):
super(series_decomp, self).__init__()
self.moving_avg = moving_avg(kernel_size, stride=1)
def forward(self, x):
moving_mean = self.moving_avg(x)
res = x - moving_mean
return res, moving_mean
class Model(nn.Module):
"""
Decomposition-Linear
"""
def __init__(self, configs):
super(Model, self).__init__()
self.seq_len = configs.seq_len
self.pred_len = configs.pred_len
# Decompsition Kernel Size
kernel_size = 25
self.decompsition = series_decomp(kernel_size)
self.individual = configs.individual
self.channels = configs.enc_in
if self.individual:
self.Linear_Seasonal = nn.ModuleList()
self.Linear_Trend = nn.ModuleList()
for i in range(self.channels):
self.Linear_Seasonal.append(nn.Linear(self.seq_len,self.pred_len))
self.Linear_Trend.append(nn.Linear(self.seq_len,self.pred_len))
# Use this two lines if you want to visualize the weights
# self.Linear_Seasonal[i].weight = nn.Parameter((1/self.seq_len)*torch.ones([self.pred_len,self.seq_len]))
# self.Linear_Trend[i].weight = nn.Parameter((1/self.seq_len)*torch.ones([self.pred_len,self.seq_len]))
else:
self.Linear_Seasonal = nn.Linear(self.seq_len,self.pred_len)
self.Linear_Trend = nn.Linear(self.seq_len,self.pred_len)
# Use this two lines if you want to visualize the weights
# self.Linear_Seasonal.weight = nn.Parameter((1/self.seq_len)*torch.ones([self.pred_len,self.seq_len]))
# self.Linear_Trend.weight = nn.Parameter((1/self.seq_len)*torch.ones([self.pred_len,self.seq_len]))
def forward(self, x):
# x: [Batch, Input length, Channel]
seasonal_init, trend_init = self.decompsition(x)
# seasonal_init: [Batch, Input length, Channel]
# trend_init: [Batch, Input length, Channel]
seasonal_init, trend_init = seasonal_init.permute(0,2,1), trend_init.permute(0,2,1)
# seasonal_init: [Batch, Channel, Input length]
# trend_init: [Batch, Channel, Input length]
if self.individual:
seasonal_output = torch.zeros([seasonal_init.size(0),seasonal_init.size(1),self.pred_len],dtype=seasonal_init.dtype).to(seasonal_init.device)
trend_output = torch.zeros([trend_init.size(0),trend_init.size(1),self.pred_len],dtype=trend_init.dtype).to(trend_init.device)
for i in range(self.channels):
seasonal_output[:,i,:] = self.Linear_Seasonal[i](seasonal_init[:,i,:])
trend_output[:,i,:] = self.Linear_Trend[i](trend_init[:,i,:])
else:
seasonal_output = self.Linear_Seasonal(seasonal_init)
trend_output = self.Linear_Trend(trend_init)
x = seasonal_output + trend_output
return x.permute(0,2,1) # to [Batch, Output length, Channel]해당 코드가 이 논문에서 주장하는 가장 대표적인 코드로 많이 소개되는 코드입니다.
series_decomp 를 할 때 kernel_size를 현재 25로 되어 있습니다. (한번에 보는 seq 개수를 25개로 함)
중간에 트릭으로 kernel_size보다 작을 경우에 앞 뒤로 처음 시점과 마지막 시점을 복사해줍니다.
데이터가 (batch_size, seq_len, channel) 이 (32,2,3) 이고 kernel_size가 25면 다음과 같은 순서로 shape이 변한다.

moving_avg class
| self.avg = nn.AvgPool1d(kernel_size=kernel_size, stride=stride, padding=0) | kernel_size = 25 , stride = 1 , X = (batch_size, seq_len, channel) (batch size = 32, seq_len= 2, channel = 3) |
| front = x[:, 0:1, :].repeat(1, (self.kernel_size - 1) // 2, 1) end = x[:, -1:, :].repeat(1, (self.kernel_size - 1) // 2, 1) x = torch.cat([front, x, end], dim=1) |
(25-2)//2 = 12 front : (32, 12,3) end : (32, 12,3) x = (32, 12+ 2 + 12 ,3) (32,26,3) |
| x = x.permute(0, 2, 1) |
(32,3,26) |
| x = self.avg(x) | ((26 + 2 x 0 - 25) / 1 + 1 ) = 2 (32,3,2) |
| x = x.permute(0, 2, 1) | (32,2,3) |
여기서 주의할 점은 kernel size는 홀수여야 한다는 것
mov_avg = moving_avg(25,stride=1)
moving_mean = mov_avg(X)
print(X.size(), moving_mean.size())
res = X - moving_mean
print(res.size(), moving_mean.size())
seasonal_init = res
trend_init = moving_mean
seasonal_init, trend_init = seasonal_init.permute(0,2,1), trend_init.permute(0,2,1)
season_layer = nn.Linear(in_seq_len, pred_len)
trend_layer = nn.Linear(in_seq_len, pred_len)
seasonal_output = season_layer(seasonal_init)
trend_output = trend_layer(trend_init)
print(seasonal_output.size(), trend_output.size(), (seasonal_output+trend_output).size())개인적인 의견
해당 구조를 통해서 간단한 모델링을 통해 쉽게 Transformer를 이길 수 있다는 것이 매우 인상 깊었다.
특히 많은 수의 파라미터를 가지다 보니, overfitting 되는 경우가 만은 것 같은데, 이걸 단순화시키고 통계 정보를 추가하니 더 잘된다라는 것이라고 생각이 든다.
그렇지만, 개인적으로는 transformer 쪽으로 이쪽 분야가 성공하면 좋을 것 같다는 생각이 든다.
이런 시계열이나 정형데이터 같은 경우, 데이터의 feature가 늘어난다던지 줄어든다던지 시간에 따라 많이 변할 수가 있는데, 이러한 부분들도 같이 학습할 수 있게 하려면, nlp에서 사용하는 토큰화된 방식을 사용해야 할 것 같다.
이 논문을 반박한 "A Time Series Is Worth 64 Words: Long-Term Forecasting With Transformer"라는 논문이 있고 여기서는 PatchTST를 제안한다.
나중에는 이 논문을 살펴보고자 한다...
참고
코드
GitHub - cure-lab/LTSF-Linear: This is the official implementation for AAAI-23 Oral paper "Are Transformers Effective for Time S
This is the official implementation for AAAI-23 Oral paper "Are Transformers Effective for Time Series Forecasting?" - GitHub - cure-lab/LTSF-Linear: This is the official implementation f...
github.com
http://dsba.korea.ac.kr/seminar/?mod=document&uid=2670
[Paper Review] A Time Series Is Worth 64 Words: Long-Term Forecasting With Transformers
[ 발표 요약 ] 1. Topic A Time Series Is Worth 64 Words: Long-Term Forecasting With Transformers 2. Overview 이번 세미나 시간에는 ICLR 2023에 accept 된 long-term time series forecasting(LTSF) 방법론 PatchTST를 공유하고자 한다.
dsba.korea.ac.kr
https://arxiv.org/abs/2211.14730
A Time Series is Worth 64 Words: Long-term Forecasting with Transformers
We propose an efficient design of Transformer-based models for multivariate time series forecasting and self-supervised representation learning. It is based on two key components: (i) segmentation of time series into subseries-level patches which are serve
arxiv.org
'ML(머신러닝) > Time Series' 카테고리의 다른 글
| TimeSeries) TSMixer 논문 및 구현 살펴보기 (5) | 2023.10.13 |
|---|---|
| TimeSeries) PatchTST 논문과 코드 살펴보기 (5) | 2023.07.12 |
| TimeSeries) Transformer 기반 Time Series Forecast 논문 알아보기 (0) | 2023.07.05 |
| Python) Vector AutoRegressive Model in Python(Difference , Inverse Transform) (0) | 2023.04.03 |
| 계절형 자기회귀 이동평균모형(SARIMA) (0) | 2018.04.09 |