2023.07.05 - [ML(머신러닝)/Time Series] - Transformer 기반 Time Series Forecast 논문 알아보기
2023.07.06 - [ML(머신러닝)/Time Series] - TimeSeries Forecast) Transformer보다 좋다는 LSTF-Linear 알아보기
2023.07.12 - [ML(머신러닝)/Time Series] - TimeSeries) PatchTST 논문과 코드 살펴보기
2023.10.13 - [분류 전체보기] - TimeSeries) TSMixer 논문 및 구현 살펴보기

해당 논문은 구글 클라우드 AI Research 팀에서 작성을 한 것이라, 믿고 보는 논문이라 생각하고 논문을 읽어보고자 한다.
현재 기준(2023.10.07) 기준으로 2023.09.11에 나온 논문으로 가장 핫 한 논문이라고 볼 수 있고, 어떤 생각을 가지고 기존 논문들과 차별점을 가지고 만들었을까 하는 궁금증을 가지고 읽어보고자 한다. (물론 현시점에서 인용수는 많지 않다)
Abstract
이 논문은 시계열 데이터를 예측하기 위한 새로운 아키텍처인 TSMixer에 대해 이야기하고 있음.
일반적으로 많이 쓰이는 딥러닝 모델들도 있지만, 이 논문은 선형 모델이나 간단한 모델도 복잡한 딥러닝 모델만큼 효과적일 수 있다고 주장함.
TSMixer는 다층 퍼셉트론(MLP)를 쌓아 만들어졌고, 시간과 특성(피처) 차원 모두를 활용하여 데이터에서 정보를 효과적으로 끌어냈다고 주장함.
이 아이디어는 실세계 데이터와 여러 벤치마크에서 상당히 효과적으로 작동하며, 이를 통해 딥러닝 기반 시계열 예측에 새로운 가능성을 제시함.
모델 아키텍처
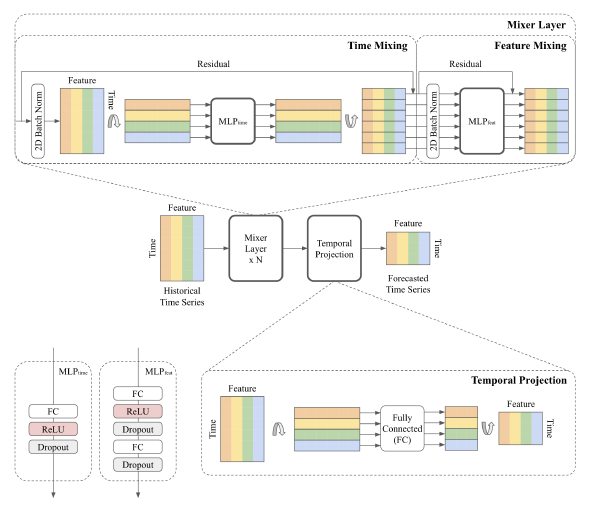
TSMixer는 다변량 시계열 예측을 위한 것이며, 여러 특성과 시간 단계를 다룸.
정보를 집계하기 위해, TSMixer는 시간-믹싱과 특성-믹싱 MLPs를 교차하여 사용함.
이 둘은 각각 모든 특성과 시간 단계 간에 공유되며, 이 설계 방식은 TSMixer가 시간과 교차 변수 정보를 효과적으로 활용하게 해서, 파라미터의 수를 제한적으로 사용하면서도 우수한 일반화 능력을 갖게 한다고 주장함.
또한 이 논문에서는 보조 정보를 활용한 확장도 함께 탐구하고 있음.
Introduction
시계열 예측은 수요 예측(상품의 수요 - Böse et al., 2017; Courty & Li, 1999), 팬데믹 확산(Zhang & Nawata, 2018), 그리고 인플레이션율(Capistrán et al., 2010)과 같이, 수많은 실세계 사용 사례에서 일반적인 문제라고 함.
시계열 데이터의 예측 가능성은 종종 세 가지 주요 측면에서 기인한다고 함.
- 지속적인 시간 패턴(Persistent temporal patterns) : 이는 시간에 따른 트렌드나 계절적인 패턴(예: 장기 인플레이션, 요일별 효과)
- 교차 변수 정보(Cross-variate information) : 여러 변수들 간의 상호 관계를 이야기해요. 예를 들어, 체중이 증가할 때 혈압이 상승하는 관계를 포함
- 보조 특성(Auxiliary features): 이는 정적인 특성과 미래의 정보(예: 제품 카테고리, 프로모션 이벤트)를 포함하고 있음
아래 그림도 해당 논문에서 나오는 3가지 주요 측면을 고려해서 만든 것으로 생각이 든다.
Historical은 Persistent temporal patterns을 표현하는 것 같고 Static은 보조 특성인 것 같은데 아래에서 나오는 Future는 Feature Mixing인 것을 보아 Cross-variate information 같긴 한데, 정확하지는 않음.
일반화된 아키텍처
전통적인 모델들, 예를 들어 ARIMA (Box 등, 1970),은 단변량 시계열에 대해 설계되었으며, 여기서는 오직 시간 정보만을 사용할 수 있음. 따라서 이들은 종종 복잡한 교차 변수 정보와 보조 특성을 포함하는 도전적인 실제 데이터를 다룰 때 제한을 가지게 됨.
반대로, 많은 딥 러닝 모델들, 특히 Transformer 기반 모델들이 복잡한 시간 패턴과 교차 변수 의존성을 모두 포착할 수 있는 능력 때문에 제안됨.(Gamboa, 2017; Li 등, 2019; Wen 등, 2017; Zhou 등, 2021; Wu 등, 2021; Lim & Zohren, 2021; Liu 등, 2022a; Zhou 등, 2022b; Liu 등, 2022b; Zhou 등, 2022a).
직관적으로는, Transformer 아키텍처를 기반으로 한 것과 같은 다변량 모델들이 교차 변수 정보를 활용할 수 있는 능력 때문에 단변량 모델들보다 더 효과적이어야 한다고 생각된다고 함. 그러나 Zeng 등(2023)은 이것이 항상 그런 것은 아니라고 밝혔습니다 - Transformer 기반 모델들은 실제로 많이 사용되는 예측 벤치마크에서 단순한 단변량 시간 선형 모델보다 상당히 나쁠 수 있는 결과가 나온다고 함.
다변량 모델들은 특히 대상 시계열이 다른 공변량과 상관되지 않을 때 과적합에서 고통을 받는 것 같습니다.
이 발견은 두 개의 핵심적인 질문을 제기하게됨.
1. 교차 변수 정보가 정말로 시계열 예측에 이점을 제공하나요?
2. 교차 변수 정보가 도움이 되지 않을 때, 다변량 모델들은 단변량 모델만큼 잘 수행될 수 있나요?
이러한 질문들에 답하기 위해, 저자들은 시간 선형 모델의 효과성(effectiveness of temporal linear models)을 분석하는 것으로 시작했다고 함.
저자의 발견은 시간 단계 종속적인 특성이 공통 가정하에 시간 패턴을 학습하기 위한 시간 선형 모델들을 좋은 후보로 만든다는 것을 나타냄.
저자는 아래와 같은 방식으로 선형 모델들의 능력을 점진적으로 증가시킴
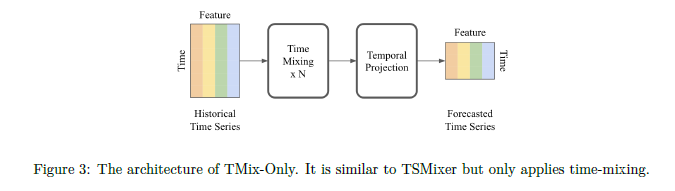
1. 비선형들과 함께 시간 선형 모델을 쌓음으로써 (TMix-Only),
2. 교차 변수 피드 포워드 계층 (TSMixer)을 도입
그 결과로 나온 TSMixer는 개념적으로 시간 혼합 및 특성 혼합 작업에 해당하는 MLP를 시간과 특성 차원에 걸쳐 교대로 적용하여, 그림 1에서 보이는 것처럼, 효과적으로 시간 패턴과 교차 변수 정보를 포착함.
residual 디자인은 TSMixer가 시간 선형 모델의 능력을 유지하면서도 교차 변수 정보를 활용할 수 있도록 보장한다고 주장함.

저자들의 실험에 따르면, TSMixer는 단변량 모델들이 다변량 모델들을 앞질렀던 데이터셋에서도 잘 동작함.
long-term forecasting datasets (Wu et al., 2021) 데이터셋들은 교차 변수 정보가 그렇게 유익하지 않아서, 단변량 모델들이 더 잘 나옴.
그럼에도, TSMixer는 단변량 모델들만큼이나 좋고, 다른 다변량 모델들보다 훨씬 더 나왔다고 함.
M5 벤치마크에서, 교차 변수 정보는 분명 큰 도움이 되고, TSMixer는 이 정보를 정말 잘 활용할 수 있음.
실제 문제에서도 TSMixer는 몇몇 인기 있는 산업적인 모델들(DeepAR, TFT) 보다 더 잘 나왔다고 함.
기여한 점
- 최첨단 선형 모델의 효과를 분석해 보고, 이들의 시간 단계 의존 특성이 흔히 있는 가정하에 시간 패턴을 학습하는 데 좋은 후보라는 걸 지적함.
- TSMixer를 제안하는데, 이는 혁신적인 구조로, 선형 모델의 시간 패턴을 포착하는 용량을 유지하면서도 교차 변수 정보를 활용할 수 있음.
- 흔히 사용되는 장기 예측 벤치마크에서 다변량 모델을 평가하는 것의 잠재적 위험을 지적함.
- 우리의 경험적 연구는 TSMixer가 흔한 벤치마크에서 단변량 모델과 맞먹고, 교차 변수 정보가 중요한 대규모 산업 애플리케이션에서 최첨단을 달성하는 첫 번째 다변량 모델이라는 걸 보여줌.
관련 연구
일반적으로, 시계열 예측은 주어진 역사적 관측치를 바탕으로 하나 또는 여러 관련 변수의 미래 값을 예측하는 작업임. 깊은 신경망이 이 작업에 대해 광범위하게 조사되어 왔음 (Zhang et al., 1998; Kourentzes, 2013; Lim & Zohren, 2021). Table 1에서는 모델이 고려하는 정보를 기반으로 주목할만한 작업을 크게 세 카테고리로 나누었음: (I) 단변량 예측, (II) 다변량 예측, 및 (III) 보조 정보와 함께하는 다변량 예측.
TSMixer 같은 경우, 카테고리 2 또는 카테고리 3에 속한다고 함.

TSMixer에 대한 우리의 동기는 시계열 예측을 위한 선형 모델의 성능을 분석하는 데서 비롯됨. 비슷한 구조들이 이전에 다른 데이터 유형들, 예를 들면 컴퓨터 비전에서 잘 알려진 MLP Mixer 구조에서 제안된 TSMixer와 같은 방식으로, 고려되었음 (Tolstikhin et al., 2021). 믹서 모델들은 또한 텍스트 (Fusco et al., 2022), 음성 (Tatanov et al., 2022), 네트워크 트래픽 (Zheng et al., 2022), 및 포인트 클라우드 (Choe et al., 2022)에 적용되었음. 그럼에도 불구하고, 최선의 우리의 지식으로는, 시계열 예측을 위한 MLP Mixer 기반 구조의 사용은 문헌에서 탐구되지 않았음.
Linear Models for Time Series Forecasting
선형 모델에 대한 디자인 이유
트랜스포머와 같은 복잡한 순차적 구조보다 선형 모델의 우월성이 Zeng 등(2023)에 의해 경험적으로 입증되었다고 함.
먼저, 다른 순차적 모델과 비교했을 때 그것의 단순함으로 인해 무시되었을 수 있는 선형 모델의 용량에 대한 이론적인 통찰을 제공함.
그다음에, 선형 모델을 다른 구조와 비교하고 선형 모델이 RNN 및 트랜스포머에는 없는 특성을 가지고 있다는 것을 보여줌 – 그들(Linear Model)은 단변량 시계열에 대한 시간 의존성을 학습하기 위한 적절한 표현 용량을 가지고 있다고 함.
이러한 발견은 저희가 제안하는 아키텍처의 디자인을 동기 부여함. 이는 Sec. 4(TSMixer Architecture)에서 제시함.
아래 표기법이 의미하는 것은 결국 X의 과거 데이터를 기반으로 선형결합을 통해 미래 T step 만큼 예측하는 함수를 만들 수 있다를 의미함.
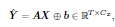

보통 많은 실제 문제에서는 시계열 예측의 경우 부드러움(smoothness)이나 주기성(periodicity) 중 하나를 가지고 있다고 함. 그렇지 않다면 예측 가능성이 낮고 예측 모델은 신뢰할 수 없을 것은
이론 3.1은 시계열(일련의 데이터 포인트들이 시간에 따라 측정된 것, 예를 들어 날씨 데이터)을 어떻게 예측할 수 있는지에 관한 것임.
여기에서 주장하는 주요 아이디어는, 실제 세계의 시계열 데이터는 대게 두 가지 주요 부분으로 나눌 수 있다는 것임
1. 주기적인 부분 (g(t)): 계속해서 반복되는 패턴을 가지고 있습니다 (예: 하루 중 일정 시간에 온도가 오르거나 내리는 것).
2. 부드러운 트렌드 (f(t)): 천천히 상승하거나 하강하는 패턴을 가지고 있습니다 (예: 매년 겨울이 점점 더 따뜻해지는 것).
이 이론은, 이 두 부분을 합치면 원래의 시계열 데이터를 얻을 수 있고, 이 두 부분을 잘 예측할 수 있으면 원래의 데이터도 잘 예측할 수 있을 거라고 말해줍니다.
쉽게 말해, 이론은 다음과 같습니다:
- \(g(t)\): 계속해서 반복되는 패턴 (예: 매일 낮에는 따뜻하고 밤에는 춥다).
- \(f(t)\): 천천히 변하는 패턴 (예: 매년 겨울이 점점 더 따뜻해진다).
우리는 이 두 패턴을 더해서 (\(x(t) = g(t) + f(t)\)) 원래의 패턴을 만듭니다. 그리고 이 두 가지 패턴 각각을 잘 예측하는 방법을 찾으면, 원래의 패턴도 잘 예측할 수 있다는 것이죠.
이론 3.1에서는, 만약 \(f(t)\)가 천천히 변하고, \(g(t)\)가 정확한 주기를 가지고 있다면 (즉, 매일, 매주, 매년 같은 패턴이 반복된다면), 그리고 우리가 충분히 많은 과거 데이터를 가지고 있다면, 이 두 패턴을 합친 데이터도 잘 예측할 수 있다는 수학적인 방법을 제시해 줍니다.
이렇게 해서, 선형 모델이라는 간단한 방법만으로도 우리가 일상에서 볼 수 있는 많은 패턴을 예측할 수 있게 도와준다는 것을 알 수 있어요!
(대략적으로 주기성과 스무스 함을 강조한다는 내용인 것 같은데... chatgpt에게 요약을 시키니 다음과 같이 잘 요약해 주는 것 같다)

선형 모델과 딥 러닝 모델 간의 차이점
고정된 가중치 vs 데이터 종속 가중치: 선형 모델은 각 타임 스텝에 대해 고정된 가중치를 가지며, 이는 "시간-스텝-종속적(time-step-dependent)"이라고 불림. 반면, 순환 및 주의 기반 아키텍처 (예: LSTMs 또는 Transformers의 attention 레이어)는 "데이터-종속적(data-dependent)" 함수의 출력으로 입력 시퀀스에 대한 가중치를 가진다고 함
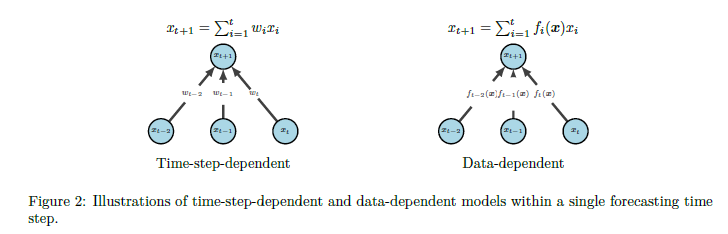
과적합의 경향: 이러한 차이로 인해, 선형 모델은 시간에 따른 패턴을 모델링하는 데 매우 효과적인 반면, 순환 및 주의 기반 아키텍처는 대표성 있는 용량에도 불구하고 타임 스텝 독립성을 달성하는 것이 어렵고, 데이터에 과적 합하는 경향이 있음.
성능 차이: 이러한 선형 모델의 독특한 특성이 Zeng et al. (2023)의 결과를 설명하는 데 도움이 될 수 있으며, 선형 모델의 성능을 따라잡는 다른 방법이 없음.
분석의 한계
고변동성과 비주기적 패턴: 실제 세계의 시계열 데이터는 고변동성을 가질 수 있고, 패턴이 주기적이거나 부드럽지 않을 수 있습니다. 이런 경우, 과거 관측 패턴만을 기반으로 하는 것은 최적이 아닐 수 있음.
Lipschitz 케이스를 넘어서의 분석: Lipschitz 케이스를 넘어서는 분석은 복잡할 수 있으며, 이 논문의 범위를 벗어날 수 있음. 이로 인해 더 복잡한 경우에 대한 분석은 미래의 더 추가적인 연구를 해봐야 한다고 함.
멀티베리어트 정보의 활용: 추가로, 다변수 정보를 효과적으로 활용하는 것의 중요성도 강조되며, 다른 공변량이 변동성을 모델링하는 데 사용될 수 있는 정보를 포함할 수 있다는 함.
TSMixer Architecture
TSMixer의 핵심 구성요소
시간 혼합(time-mixing) 연산: 시계열 데이터의 시간적인 특성과 의존성을 모델링함
특성 혼합(feature-mixing) 연산: 다양한 특성(variates) 간의 관계를 모델링함
이 두 연산은 TSMixer 아키텍처의 기본 구성요소로, 이들은 교차하면서 효과적으로 시간과 피처 정보를 모두 활용함
TSMixer의 특징
효율적인 자원 활용: 시간 의존성과 크로스-베리어트(cross-variate) 정보를 동시에 활용하면서, 계산 복잡성과 모델 크기를 제한함.
긴 lookback window 활용: TSMixer는 긴 lookback window를 사용할 수 있으며, O(L + C)의 파라미터 성장률을 유지함, 만약 완전히 연결된(fully-connected) MLPs를 사용한다면 O(LC)이 될 것임
TMix-Only: TSMixer의 단순화된 변형
TSMixer 아키텍처의 단순화된 버전으로, 오로지 시간 혼합 연산만을 사용함.
각 변수(variate)에 걸쳐 공유되는 잔여(residual) MLP로 구성되어 있음.
확장성
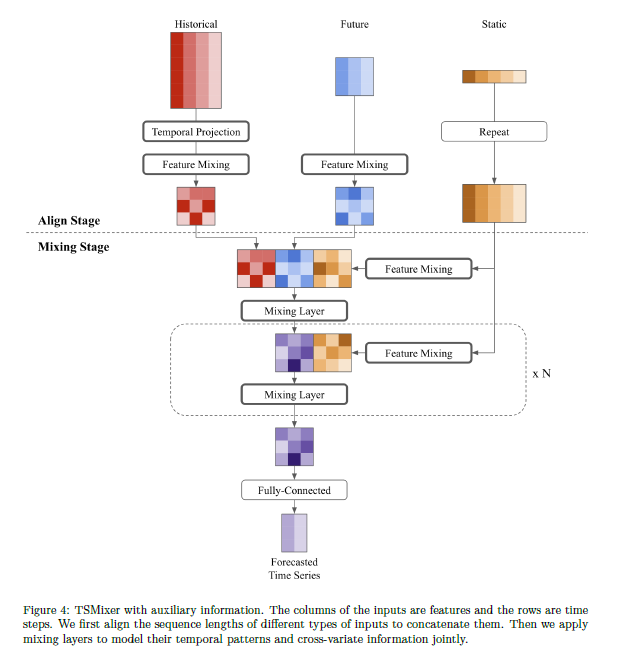
TSMixer는 시계열 데이터에 대한 보조 정보(auxiliary information)가 사용 가능한 시나리오로 확장할 수 있음.
TSMixer for Multivariate Time Series Forecasting
시간 혼합 MLP: 시간 혼합 MLPs는 시계열의 시간 패턴을 모델링함. 이것들은 완전히 연결된 층, 활성화 함수, 그리고 드롭아웃으로 구성됨. 이들은 입력을 전치하여 시간 도메인을 따라 완전히 연결된 계층을 적용하고 특성에 의해 공유됨. 우리는 단일 계층 MLP를 사용하는데, 3절에서 볼 수 있듯이, 간단한 선형 모델만으로도 복잡한 시간 패턴을 학습하기 위한 강력한 모델이 될 수 있음이 입증되었다고 주장함
특성 혼합 MLP: 특성 혼합 MLPs는 시간 스텝에 의해 공유되며, 공변량 정보를 활용하는 데 사용됨. 트랜스포머 기반 모델과 유사하게, 우리는 복잡한 특성 변환을 학습하기 위해 두 층의 MLP를 고려함.
시간 투영: 시간 투영은 Zeng et al. (2023)에서 선형 모델들과 동일하게, 시간 도메인에 적용되는 완전히 연결된 층임.
이들은 시간 패턴을 학습할 뿐만 아니라, 시계열을 원래의 입력 길이 L에서 목표 예측 길이 T로 매핑함
잔여 연결: 우리는 각 시간 혼합과 특성 혼합 층 사이에 잔여 연결을 적용함. 이 연결들은 모델이 더 효과적으로 깊은 구조를 학습하게 하고, 불필요한 시간 혼합 및 특성 혼합 연산을 효과적으로 무시하게 함.
정규화: 정규화는 딥 러닝 모델 훈련을 향상하는 일반적인 기술임. 배치 정규화와 계층 정규화 간의 선호도는 작업에 의존적이지만, Nie et al. (2023)은 일반 시계열 데이터셋에서 배치 정규화의 이점을 보여줌. 특성 차원에 일반적으로 적용되는 일반적인 정규화와 대조적으로, 우리는 시간 혼합과 특성 혼합 연산의 존재로 인해 시간 및 특성 차원에 2D 정규화를 적용합니다.(개인적으로 특이하다고 생각했던 부분)
비록 TSMixer의 구조가 상대적으로 간단하지만, 실험을 보면, TSMixer가 대표적인 벤치마크에서 최첨단 모델과 경쟁력 있음을 보여줌.
보조 정보를 가진 시계열 예측을 위한 확장된 TSMixer
이 아키텍처는 시계열 예측에 추가적인 정보를 사용할 수 있도록 확장되었음. 실세계 시나리오에서는 과거의 데이터뿐만 아니라 정적인 정보(예: 위치)와 미래의 변동하는 특성(예: 다가오는 주의 프로모션)도 사용할 수 있음. 또한 이 문제는 여러 시계열로 확장될 수 있으며, 각 시계열은 자체적인 특성 세트를 가질 수 있음.
이 아키텍처는 다른 종류의 특성들을 활용하기 위해 설계되었고, "정렬" 단계와 "혼합" 단계로 구성됨
정렬 단계: 과거와 미래의 특성을 동일한 형태로 정렬하고, 정적 특성도 해당 형태에 맞춰 변형함. 이는 모든 특성이 같은 형태를 가지고 있어야 함으로써 혼합 단계에서 함께 처리될 수 있게 함.
혼합 단계: 모든 특성에서 시간 패턴과 교차 변수 정보를 이용하도록 설계되었음. 이 단계에서는 시간 및 특성을 혼합하는 연산이 포함되어 있음.
마지막으로, 완전히 연결된 층이 각 타임 스텝에 대한 출력을 생성함. 이 출력은 시계열의 예측된 실제 값일 수도 있고, 일부 작업(예: 소매 수요 예측)에서는 목표 분포의 매개변수를 생성할 수도 있음. 이러한 확장된 TSMixer 구조는 다양한 종류의 정보를 함께 사용하여 시계열을 예측하는 데에 사용할 수 있음.
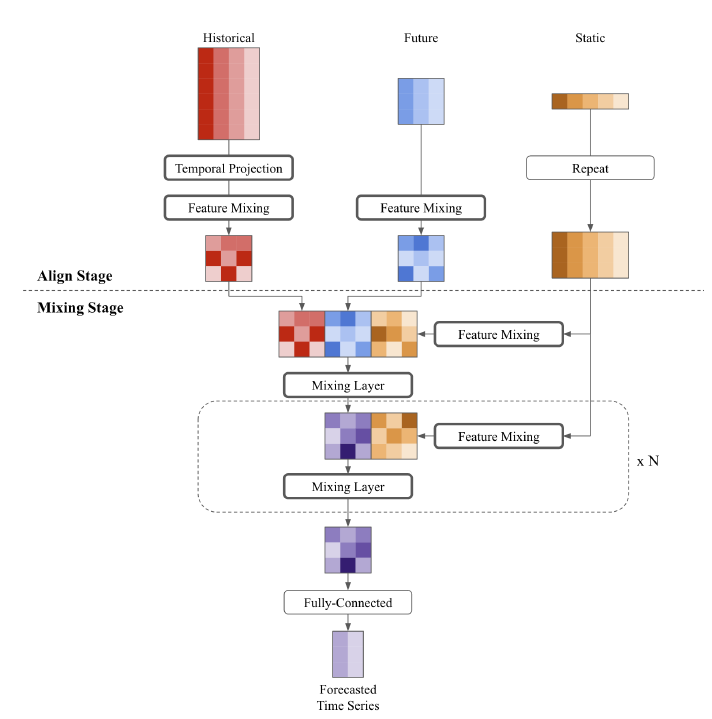
Differences between TSMixer and MLP-Mixer
TSMixer는 MLP-Mixer와 아키텍처적 유사성을 공유하지만, 위의 방법론 중에서 3에서의 분석에 기반한 TSMixer의 개발은 고유한 정규화 방법을 도출하였습니다. TSMixer에서 두 차원은 MLP-Mixer의 특성 및 패치와 달리, 특성과 시간 단계를 나타냅니다. 그 결과, 특성과 시간 단계 간의 규모를 유지하기 위해 2D 정규화를 적용하고 있으며, 이는 예측에서 시간 패턴의 중요성을 발견했기 때문입니다.
또한, 실세계 시나리오에서 최첨단 결과를 달성하기 위해 필수적인 이기종 입력(heterogeneous)으로부터 정보를 더 잘 추출하기 위해 TSMixer의 확장 버전을 제안하고 있습니다. 이 확장 버전은 다양한 입력 유형에서 정보를 더 효과적으로 추출하도록 설계되어 있습니다.
실험
다양한 애플리케이션: 이는 날씨, 전기, 트래픽과 같은 다양한 애플리케이션을 포함하며, 부가 정보가 없는 다변량 시계열 데이터로 구성되어 있음.
M5 데이터 세트: 이 데이터 세트는 Walmart에서 다양한 품목의 판매를 예측하는 경쟁 작업을 위한 것임. 이는 30,490개의 시계열과 정적 특성(예: 매장 위치) 및 시간에 따라 변하는 특성(예: 캠페인 정보)을 포함한 대규모 데이터 세트임.
M5 데이터 세트는 교차 변수 정보와 부가 특성의 잠재적인 이점을 탐구하기 위한 더 도전적인 벤치마크로 여겨지고 있습니다. 이 데이터의 통계는 표에서 제시됨.
요약하면, 이 텍스트는 시계열 데이터 세트들의 사용과 그 데이터가 어떻게 구성되어 있는지에 대한 정보를 제공함.
M5 데이터 세트는 그 복잡성으로 인해 다변량 정보와 추가 특성을 활용하는 데 특히 도전적인 작업을 제공함.
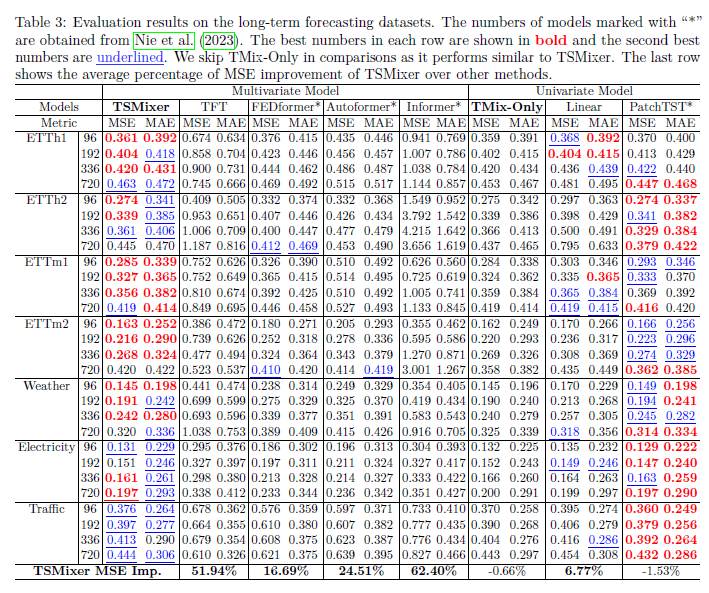
결과는 보면 결국 자기네가 우수한 경우가 있다는 실험 결과를 보여줌
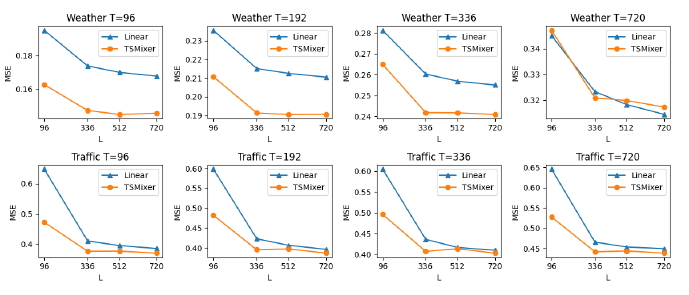
시퀀스 길이를 크게 하면 할수록 성능이 좋아진다는 사실을 확인했다고 함.
TSMixer의 더 긴 시퀀스를 활용하는 능력에 대한 더 깊은 이해를 얻기 위해, 저자는 특히 L = {96, 336, 512, 720}인 lookback window 크기를 변화시키면서 실험을 수행함. TSMixer는 window 크기가 336이나 512로 설정될 때 최상의 성능을 달성하며, window 크기가 720으로 증가하면 성능이 유사한 수준을 유지함.
다른 다변량 모델들과 비교하여, TSMixer는 더 긴 시퀀스를 활용하고 다른 다변량 모델들보다 더 나은 일반화 능력을 보여줌
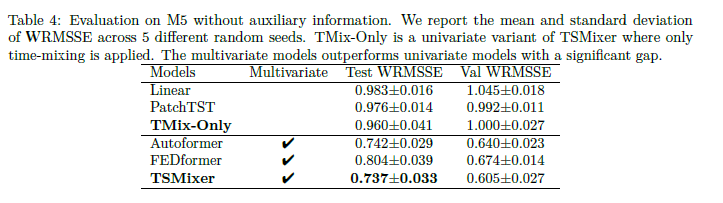
아래 결과를 보면 Feature Mixing을 쓰냐 안 쓰냐에 따라 유의미한 차이가 난다는 것을 확인한 결과임
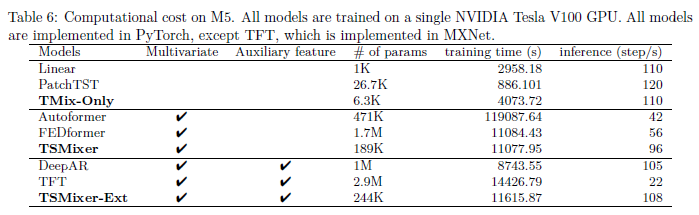
훈련 시간과 추론 속도에 따라 나온 결과이다.
다른 방법론들에 비해서 더 적은 파라미터를 가지고 유사한 성능을 낼 수 있다는 것을 주장함.
결론
TSMixer는 시계열 예측을 위한 새로운 구조로, 고급 일반화를 얻기 위해 일반적으로 사용되는 RNN(Recurrent Neural Networks)과 주의 메커니즘 대신 MLP(Multilayer Perceptrons)를 사용하여 설계되었음. 다양한 실제 시계열 예측 작업의 결과는 TSMixer가 다변량 시계열을 위한 장기 예측 벤치마크와 실제 대규모 소매 수요 예측 작업에서 모두 매우 효과적이라는 것을 보여줌. 특히, TSMixer는 장기 시계열 예측 벤치마크에서 일변량 모델과 유사한 성능을 달성할 수 있는 유일한 다변량 모델입니다. 이 구조는 더 나아가서 개선될 중요한 잠재력을 가지고 있으며, 시계열 예측 작업의 광범위한 범위에서 유용할 것으로 생각됨. 잠재적인 미래의 작업 중 일부로는 TSMixer의 해석 가능성을 더 깊게 탐구하고, 심지어 더 큰 데이터 세트에 대한 확장성을 조사하는 것이 포함될 수 있음. 이 작업이 시계열 예측을 위한 더 혁신적인 구조의 기초를 마련하기를 희망한다고 함.
구현 상세
(개인적으로 왜 이런 식으로 사용하게 됐는지가 궁금해서 보기로 함)
B.1 정규화
구현에서 사용되는 세 가지 유형의 정규화가 있습니다:
1. **전역 정규화(Global normalization):** 전역 정규화는 모든 변동성을 독립적으로 표준화하여 데이터 전처리를 수행합니다. 표준화된 데이터는 그다음 훈련과 평가에 사용됩니다. 다양한 변량의 척도에 따른 영향으로부터 예방하기 위해 장기 시계열 예측 실험에서 흔한 설정입니다. M5의 경우, 목표 시계열(판매)이 하나만 있으므로 전역 정규화를 적용하지 않습니다.
2. **지역 정규화(Local normalization):** 전역 정규화와 대조적으로, 지역 정규화는 전처리 또는 후처리로 각 배치에 적용됩니다. 장기 예측 데이터 세트의 경우, 최첨단 결과와의 공정한 비교를 보장하기 위해 가역적 인스턴스 정규화(Kim et al., 2022)를 적용합니다. M5에서는 모든 제품의 판매를 모델 입력을 위해 평균으로 독립적으로 척도를 조정하고 모델 출력을 다시 척도로 조정합니다.
3. **모델 레벨 정규화(Model-level normalization):** (Nie et al., 2023)에서 제안한 것처럼 장기 예측 데이터 세트에 배치 정규화를 적용하고 아래에서 설명한 대로 M5에 계층 정규화를 적용합니다.
이 세 가지 정규화 유형은 각각 데이터와 모델의 다양한 측면에 영향을 주며, 구현 및 실험 과정에서 다양한 척도 및 분포의 데이터를 처리하고, 모델이 서로 다른 특성과 시간 단계에서의 동적인 변화에 효과적으로 적응할 수 있도록 합니다.
B.3.1 TSMixer Components

코드
Tensorflow (논문 저자가 작성한 코드)
아래 깃헙 링크를 가면 다른 방식으로 구현한 코드도 존재함.
# coding=utf-8
# Copyright 2023 The Google Research Authors.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
"""Implementation of TSMixer."""
import tensorflow as tf
from tensorflow.keras import layers
def res_block(inputs, norm_type, activation, dropout, ff_dim):
"""Residual block of TSMixer."""
norm = (
layers.LayerNormalization
if norm_type == 'L'
else layers.BatchNormalization
)
# Temporal Linear
x = norm(axis=[-2, -1])(inputs)
x = tf.transpose(x, perm=[0, 2, 1]) # [Batch, Channel, Input Length]
x = layers.Dense(x.shape[-1], activation=activation)(x)
x = tf.transpose(x, perm=[0, 2, 1]) # [Batch, Input Length, Channel]
x = layers.Dropout(dropout)(x)
res = x + inputs
# Feature Linear
x = norm(axis=[-2, -1])(res)
x = layers.Dense(ff_dim, activation=activation)(
x
) # [Batch, Input Length, FF_Dim]
x = layers.Dropout(dropout)(x)
x = layers.Dense(inputs.shape[-1])(x) # [Batch, Input Length, Channel]
x = layers.Dropout(dropout)(x)
return x + res
def build_model(
input_shape,
pred_len,
norm_type,
activation,
n_block,
dropout,
ff_dim,
target_slice,
):
"""Build TSMixer model."""
inputs = tf.keras.Input(shape=input_shape)
x = inputs # [Batch, Input Length, Channel]
for _ in range(n_block):
x = res_block(x, norm_type, activation, dropout, ff_dim)
if target_slice:
x = x[:, :, target_slice]
x = tf.transpose(x, perm=[0, 2, 1]) # [Batch, Channel, Input Length]
x = layers.Dense(pred_len)(x) # [Batch, Channel, Output Length]
outputs = tf.transpose(x, perm=[0, 2, 1]) # [Batch, Output Length, Channel])
return tf.keras.Model(inputs, outputs)Pytorch (위의 코드 기반으로 구현해보기)
아래와 같은 느낌으로 구현할 수 있지 않을까 싶다.
class ResBlock(nn.Module):
def __init__(self, input_dim, seq_len, ff_dim, dropout_rate, norm_type="L", activation="gelu"):
super(ResBlock, self).__init__()
if norm_type == "L":
self.norm1 = nn.LayerNorm([seq_len, input_dim])
self.norm2 = nn.LayerNorm([seq_len, input_dim])
elif norm_type == "B":
self.norm1 = nn.BatchNorm1d(input_dim)
self.norm2 = nn.BatchNorm1d(input_dim)
else:
raise ValueError("norm_type should be either 'L' or 'B'")
self.linear_temporal = nn.Linear(seq_len, seq_len)
self.linear_feature1 = nn.Linear(input_dim, ff_dim)
self.linear_feature2 = nn.Linear(ff_dim, input_dim)
self.dropout = nn.Dropout(dropout_rate)
self.act = activation_functions[activation]()
def forward(self, x):
# Temporal Linear
res = self.time_mixer(x)
# Feature Linear
res = self.feature_mixer(res.transpose(1, 2))
return res
def time_mixer(self, x):
if isinstance(self.norm1, nn.BatchNorm1d):
x_temp = self.norm1(x.transpose(1, 2))
else:
x_temp = self.norm1(x)
# x_temp = self.norm1(x)
x_temp = self.linear_temporal(x_temp.transpose(1, 2))
x_temp = self.act(x_temp)
x_temp = self.dropout(x_temp)
# [bs, input_dim, seq_len]
return x.transpose(1, 2) + x_temp
def feature_mixer(self, x):
if isinstance(self.norm2, nn.BatchNorm1d):
x_feat = self.norm2(x.transpose(1, 2)).transpose(1, 2)
else:
x_feat = self.norm2(x)
x_feat = self.linear_feature1(x_feat)
x_feat = self.act(x_feat)
x_feat = self.dropout(x_feat)
x_feat = self.linear_feature2(x_feat)
x_feat = self.dropout(x_feat)
return x + x_feat
class TSMixer(nn.Module):
def __init__(
self,
input_dim,
seq_len,
norm_type,
n_block,
dropout,
ff_dim,
target_slice,
):
super(TSMixer, self).__init__()
self.blocks = nn.ModuleList([ResBlock(input_dim, seq_len, ff_dim, dropout, norm_type) for _ in range(n_block)])
self.target_slice
self.target_linear_out = nn.ModuleList()
# 변형해봄(타겟마다 마지막 레이를 다르게)
for i in range(len(self.target_slice)):
self.target_linear_out.append(nn.Linear(seq_len, pred_len, bias=True))
def forward(self,x):
for block in self.blocks:
x = block(x)
x = x[:, :, self.target_slice]
bs = x.size(0)
x = x.transpose(-2, -1) # [Batch, Channel, Input Length]
# x = self.linear_out(x) # [Batch, Channel, Output Length]
x_out = torch.zeros(bs, len(self.target_slice), device=x.device)
for idx, linear_out in enumerate(self.target_linear_out):
x_out[:, [idx]] = linear_out(x[:, idx, :])
return x_out
개인 의견
요즘따라 좀 더 간단하게 시계열을 풀 수 있다는 식의 논문들이 나오는 것 같고, 원인으로는 여기서 나온 Lipschitz 케이스인 경우가 시계열 데이터 상황에 많이 발생하다 보니 이런 식으로 논문들이 많이 나온다고 생각한다.
개인적으로도 Transformer가 그런 부분에서는 약하다고는 생각이 들지만, 외부 조건에 따라서 변화하는 문제를 예측해야 할 경우, 해당 방법론으로 예측이 잘 되지 모르겠다.
현재 풀고자 하는 문제에 최근에 딥러닝 방법론들인 linear 계열(tsmixer, dliear 등)을 시도해보고 있지만 , 만족할 만한 결과는 나오지 못하고 있다 ㅠㅠ (물론 Transformer 계열의 방법도 좋지 않고, RNN 계열이 다른 것 대비해서 잘 나오고 있다)
참고
https://github.com/google-research/google-research/blob/master/tsmixer/tsmixer_basic/models/tsmixer.py
https://arxiv.org/abs/2303.06053
TSMixer: An All-MLP Architecture for Time Series Forecasting
Real-world time-series datasets are often multivariate with complex dynamics. To capture this complexity, high capacity architectures like recurrent- or attention-based sequential deep learning models have become popular. However, recent work demonstrates
arxiv.org
'ML(머신러닝) > Time Series' 카테고리의 다른 글
| TimeSeries) PatchTST 논문과 코드 살펴보기 (5) | 2023.07.12 |
|---|---|
| TimeSeries) Transformer보다 좋다는 LSTF-Linear 알아보기 (0) | 2023.07.06 |
| TimeSeries) Transformer 기반 Time Series Forecast 논문 알아보기 (0) | 2023.07.05 |
| Python) Vector AutoRegressive Model in Python(Difference , Inverse Transform) (0) | 2023.04.03 |
| 계절형 자기회귀 이동평균모형(SARIMA) (0) | 2018.04.09 |