VAR 모형을 모델링할 때 정상성을 만족하기 위해서 차분을 하게 되는데, 이러한 과정에서 역변환하는 것에 대해서 헷갈리는 점이 있어서 이 코드를 짜보게 됐다,
chatgpt에 여러 번 코드 짜는 것을 요청했지만, prompt가 문제가 있어서 그런 지 몰라도 잘 못해줘서, 구현을 다시 해봤다.
오히려 chatgpt를 믿고 코딩을 해보다 보니, 실패가 나오고, 실패로 인해서 코드를 분석하는 그 과정이 오히려 내가 이해를 하는데 있어서, 더 어렵게 한 점이 있었다 ㅠㅠ
일단 차분에 대해서이해를 해보면 다음과 같다.
공식은 아래와 같다.

그러면 여기서 차분되기 전으로 돌아가려면 다음과 같이 하면 될 것이다.

그럼 여기서 알아야 하는 규칙이 차분 후의 결과의 기존 차분되기 전에 이전 시점의 데이터가 필요하다는 것을 알게 된다.
그러면 2차 차분한 것을 다시 기존 차분으로 돌리게 하려면 어떻게 해야 할까?


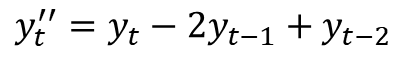
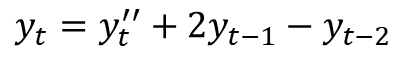
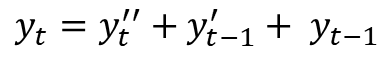
이런 식으로 얻을 수 있게 된다.
이차 차분 결과 그리고 이전 시점의 1차 차분 및 이전 시점의 데이터를 이용하면 기존 데이터의 값을 얻을 수 있다.
생각보다 규칙이 잘 보이지 않는다.
그래서 가장 쉬운 것은 1차 차분을 재귀적으로 반복하는 것이 낫다고 생각이 들었다.
그러면 우리가 매번 특정 시점의 역벽화된 예측값을 알기 위해서 이전 시점의 시점값을 알아야 하는 가에 대한 의문이 생길 수 있다.
실제로 계산해 보면 그렇지 않다는 것을 알 수 있다.

위의 식처럼 결국 예측 시점에서의 초기 시점을 알고 있다면, 그 이후에 값은 차분된 값을 이용해서 알 수 있다는 것이다.
예를 들어 아래처럼 14 시점을 예측한다고 했을 때 초기 시작이 11이라면 12,13,14의 차분된 값만 알면 된다는 것이다.
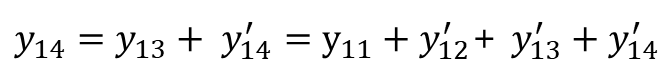
필자는 이런 재귀적인 구조와 위와 같은 규칙(누적)을 활용해서 함수로 만들어봤다.
pandas를 이용해서 해봤다. 조금만 변형하면 아마 numpy로도 가능해 보인다.
from statsmodels.tsa.statespace.tools import diff
def inv_diff_transform(raw_data:pd.DataFrame , pred :pd.DataFrame, order:int) :
order_init = {}
for idx, i in enumerate(reversed(range(1,order))) :
order_init[i] = diff(raw_data, k_diff=i).iloc[idx,:]
for i in reversed(sorted(list(order_init.keys()))) :
pred = order_init[i] + pred.cumsum()
inv = raw_data.iloc[order-1,:] + pred.cumsum()
return inv간단한 예시는 다음과 같다.
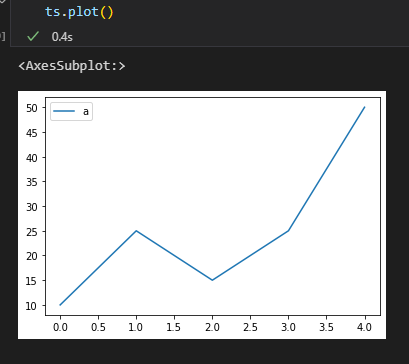
ts = pd.DataFrame([10,25,15,25,50],columns=['a'])
td_diff = diff(ts, k_diff=3)
td_diff위와 같은 그림이 있다고 했을 때 차분을 3차까지 하면 다음과 같이 된다.
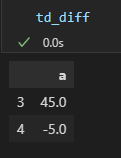
그럼 ts_diff를 알고 있고, 기존의 원자료를 3차니까 3개만 알고 있으면 된다.
그럼 위의 함수를 통해 다음과 같이 구할 수 있다.
inv_diff_transform(ts.iloc[:3,:], td_diff, 3)위의 코드를 통해 다시 원래 자료를 얻은 것을 알 수 있다.
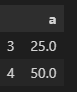
실제 예시를 이용해서 해보자.
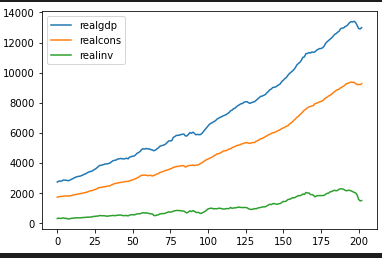
이 3개의 선을 이제 예측해 보는 작업을 해보자.
일단 차분은 2차까지 진행해 보자.
정상성 검정을 해서 하면 좋지만, 여기서는 일단 2차라고 가정하고 해 보자.
import pandas as pd
import numpy as np
from statsmodels.tsa.api import VAR
from statsmodels.tsa.statespace.tools import diff
# 데이터 불러오기
macrodata = pd.read_csv('https://raw.githubusercontent.com/statsmodels/statsmodels/master/statsmodels/datasets/macrodata/macrodata.csv')
macrodata = macrodata[['realgdp', 'realcons', 'realinv']]
# 차분 수행
order = 2
macrodata_diff = diff(macrodata, k_diff=order)이제 차분된 데이터를 이용해서 VAR 모형을 만들어보자. lag는 일단 5로 해보자.
그리고 예측은 10개 시점까지 수행해 본다.
# VAR 모델 학습
model = VAR(macrodata_diff)
results = model.fit(maxlags=5, ic='aic') # 최적의 lag를 AIC 기준으로 선택
# 테스트 데이터 예측 (10개 시점)
pred = results.forecast(macrodata_diff.iloc[-12:,].values[-results.k_ar:], 10)
pd.DataFrame(pred,columns=macrodata.columns).plot()
이렇게 하다 보면, 결과가 우리가 생각한 거랑 다르게 나온다.
바로 VAR가 예측한 것은 원자료가 아닌 2차 차분된 것을 예측하기 때문이다.
그래서 이 결과를 다시 원래대로 바꿔주는 것이 필요하다.
예측할 때 시점이 기존 데이터에 12 시점 뒤에 있는 것을 하였고, order 가 3이었으니깐 -15:-12에 있는 데이터를 사용하였다.
pred = pd.DataFrame(pred,columns=macrodata.columns)
inv_diff_transform(raw_data=macrodata.iloc[-12-3:-12,] ,pred=pred,order=3)결과 비교
pred = pd.DataFrame(pred,columns=macrodata.columns)
inv_pred_result = inv_diff_transform(raw_data=macrodata.iloc[-12-3:-12,] ,pred=pred,order=3)
np.mean((inv_pred_result.values - macrodata.iloc[-12:-2,:].values)**2)
# 7179096.364288268
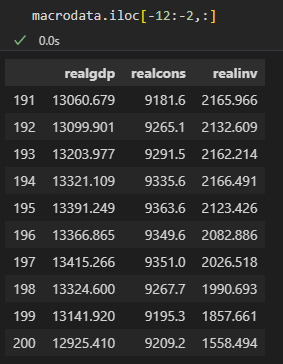

결과는 다음과 같이 나온다.
예측 결과라서 실제와 오차가 존재하지만, 실제값을 넣게 되면, 오차가 없게 나오는 것을 알 수 있다.
pred = macrodata_diff.iloc[-12:-2,:]
inv_pred_result = inv_diff_transform(raw_data=macrodata.iloc[-12-2:-12,] ,pred=pred,order=2)
np.mean((inv_pred_result.values - macrodata.iloc[-12:-2,:].values)**2)
# 0.0
이런 식으로 VAR 모형에서 차분된 데이터를 이용해서 모델링 후 예측 결과를 실제 결과로 역변환하는 것을 알아봤다.
생각보다 chatgpt를 이용해서 금방 끝날 것 같았는데, 코드에 대한 오류가 많아서 아쉬움을 느꼈다.
VAR 가 생각보다 나쁘지 않는 모델인 것 같아서 공부해봤는데, 좀 더 나중에는 실제 데이터에도 적용해보고자 한다.
'ML(머신러닝) > Time Series' 카테고리의 다른 글
| TimeSeries) Transformer보다 좋다는 LSTF-Linear 알아보기 (0) | 2023.07.06 |
|---|---|
| TimeSeries) Transformer 기반 Time Series Forecast 논문 알아보기 (0) | 2023.07.05 |
| 계절형 자기회귀 이동평균모형(SARIMA) (0) | 2018.04.09 |
| ARIMA 모형의 적합 (0) | 2018.03.25 |
| 단위근과 단위근 검정 (0) | 2018.03.25 |