이전에는 도입부로 설명했다면, 이번에는 bayesian regression pyro에서 어떻게 할 수 있는지 알아봅니다.
목표는 데이터 세트의 두 가지 기능인 국가의 1인당 로그 GDP를 다시 한 번 예측하는 것입니다.
국가가 아프리카에 있는지 여부와 지형 견고성(Terrian Ruggedness) 지수입니다.
참고 자료
2022.08.21 - [분석 Python/Pyro] - [Pyro] Application - 1. Bayesian Regression 이해하기
2022.08.28 - [분석 Python/Pyro] - [Pyro] Application - 2. Bayesian Regression 이해하기 2
2022.08.28 - [분석 Python/Pyro] - [Pyro] Application - 3. Gaussian Process 이해하기
2022.08.29 - [분석 Python/Pyro] - [Pyro] Application - 5. GP Bayesian Optimization
Load Libray and Data
import logging
import os
import torch
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from torch.distributions import constraints
import pyro
import pyro.distributions as dist
import pyro.optim as optim
pyro.set_rng_seed(1)
assert pyro.__version__.startswith('1.8.1')
%matplotlib inline
plt.style.use('default')
logging.basicConfig(format='%(message)s', level=logging.INFO)
smoke_test = ('CI' in os.environ)
pyro.set_rng_seed(1)
DATA_URL = "https://d2hg8soec8ck9v.cloudfront.net/datasets/rugged_data.csv"
rugged_data = pd.read_csv(DATA_URL, encoding="ISO-8859-1")
Model + Guide
이전에 했던 것과 동일하게 모델을 작성하지만, 이번에 사용할 때는 PyroModule 없이 작성했습니다.
동일한 사전 정보를 사용하여 회귀에서 각 항을 작성할 것입니다.
bA와 bR은 is_cont_africa와 견고성(ruggedness)에 해당하는 회귀 계수이고, a는 절편이며, bAR은 두 특징 사이의 상관 계수이다.
아래 코드를 보면 각 파라미터에 대해서 분포를 가정하는 과정을 model 함수에서 진행을 하고, 실측값들은 그대로 사용하는 그대로 사용합니다.
guide에서는 위와 동일하지만 학습할 파라미터를 다시 한번 설정해주는 부분입니다.
노말 분포를 가정하였기 때문에 학습해야 할 값들은 loc 와 scale이라서 각각 설정해줍니다.
def model(is_cont_africa, ruggedness, log_gdp):
a = pyro.sample("a", dist.Normal(0., 10.))
b_a = pyro.sample("bA", dist.Normal(0., 1.))
b_r = pyro.sample("bR", dist.Normal(0., 1.))
b_ar = pyro.sample("bAR", dist.Normal(0., 1.))
sigma = pyro.sample("sigma", dist.Uniform(0., 10.))
mean = a + b_a * is_cont_africa + b_r * ruggedness + b_ar * is_cont_africa * ruggedness
with pyro.plate("data", len(ruggedness)):
pyro.sample("obs", dist.Normal(mean, sigma), obs=log_gdp)
def guide(is_cont_africa, ruggedness, log_gdp):
a_loc = pyro.param('a_loc', torch.tensor(0.))
a_scale = pyro.param('a_scale', torch.tensor(1.),
constraint=constraints.positive)
sigma_loc = pyro.param('sigma_loc', torch.tensor(1.),
constraint=constraints.positive)
weights_loc = pyro.param('weights_loc', torch.randn(3))
weights_scale = pyro.param('weights_scale', torch.ones(3),
constraint=constraints.positive)
a = pyro.sample("a", dist.Normal(a_loc, a_scale))
b_a = pyro.sample("bA", dist.Normal(weights_loc[0], weights_scale[0]))
b_r = pyro.sample("bR", dist.Normal(weights_loc[1], weights_scale[1]))
b_ar = pyro.sample("bAR", dist.Normal(weights_loc[2], weights_scale[2]))
sigma = pyro.sample("sigma", dist.Normal(sigma_loc, torch.tensor(0.05)))
mean = a + b_a * is_cont_africa + b_r * ruggedness + b_ar * is_cont_africa * ruggednesssummary 함수는 샘플을 뽑고 나서 percentile을 계산하는 함수입니다.
# Utility function to print latent sites' quantile information.
def summary(samples):
site_stats = {}
for site_name, values in samples.items():
marginal_site = pd.DataFrame(values)
describe = marginal_site.describe(percentiles=[.05, 0.25, 0.5, 0.75, 0.95]).transpose()
site_stats[site_name] = describe[["mean", "std", "5%", "25%", "50%", "75%", "95%"]]
return site_stats학습에 사용할 데이터를 전처리 합니다.
1. 결측치 제거
2. 타깃 rgdppc_2000을 log scale 적용 (적용한 이유는 긴 꼬리 형태이기 때문에 이것을 model에서 정한 노말 분포로 맞추기 위해서는 log scale을 통해 노말 분포로 맞춰줌)
# Prepare training data
df = rugged_data[["cont_africa", "rugged", "rgdppc_2000"]]
df = df[np.isfinite(df.rgdppc_2000)]
df["rgdppc_2000"] = np.log(df["rgdppc_2000"])
train = torch.tensor(df.values, dtype=torch.float)
SVI
추론을 수행하기 위해서 SVI(Stochastic Variational Inference)를 사용합니다.
여기서 데이터 개수가 적으니까 step에는 전체 데이터를 다 넣어서 하지만, 만약 데이터가 너무 많다면, 부분적으로 샘플링해서 batch 단위로도 진행할 수 있습니다.
from pyro.infer import SVI, Trace_ELBO
svi = SVI(model,
guide,
optim.Adam({"lr": .05}),
loss=Trace_ELBO())
is_cont_africa, ruggedness, log_gdp = train[:, 0], train[:, 1], train[:, 2]
pyro.clear_param_store()
num_iters = 5000 if not smoke_test else 2
for i in range(num_iters):
elbo = svi.step(is_cont_africa, ruggedness, log_gdp)
if i % 500 == 0:
logging.info("Elbo loss: {}".format(elbo))Elbo loss: 5795.467590510845
Elbo loss: 415.8169444799423
Elbo loss: 250.71916329860687
Elbo loss: 247.19457268714905
Elbo loss: 249.2004036307335
Elbo loss: 250.96484470367432
Elbo loss: 249.35092514753342
Elbo loss: 248.7831552028656
Elbo loss: 248.62140649557114
Elbo loss: 250.4274433851242
이제 학습된 model과 guide를 통해서 학습된 파라미터에 대해서 샘플링을 해봅니다.
즉 우리가 학습한 파라미터에 대한 분포를 이용하여 데이터를 샘플링하는 것입니다.
from pyro.infer import Predictive
num_samples = 1000
predictive = Predictive(model, guide=guide, num_samples=num_samples)
svi_samples = {k: v.reshape(num_samples).detach().cpu().numpy()
for k, v in predictive(log_gdp, is_cont_africa, ruggedness).items()
if k != "obs"}
list(svi_samples.keys())
# ['a', 'bA', 'bR', 'bAR', 'sigma']뽑힌 샘플 데이터를 기반으로, sumamry 함수에 넣어서 각 값에 대한 percentile을 계산합니다.
for site, values in summary(svi_samples).items():
print("Site: {}".format(site))
print(values, "\n")Site: a
mean std 5% 25% 50% 75% 95%
0 9.177024 0.059607 9.078109 9.140462 9.17821 9.217097 9.271518
Site: bA
mean std 5% 25% 50% 75% 95%
0 -1.890622 0.122805 -2.088489 -1.979106 -1.887475 -1.803683 -1.700853
Site: bR
mean std 5% 25% 50% 75% 95%
0 -0.157847 0.039538 -0.22324 -0.183672 -0.157872 -0.133102 -0.091713
Site: bAR
mean std 5% 25% 50% 75% 95%
0 0.304515 0.067683 0.194583 0.259464 0.304908 0.348932 0.415128
Site: sigma
mean std 5% 25% 50% 75% 95%
0 0.902898 0.047971 0.824166 0.870317 0.901982 0.935171 0.981577HMC (Hamiltonian Monte Carlo)
잠재 변수(latent variable)에 대한 대략적인 사후 추론을 제공하는 변형 추론(variational inference)을 사용하는 것과 달리,
Pyro에서는 한계에서 진정한 사후로부터 편향되지 않은 샘플을 도출할 수 있는 알고리즘인 마르코프 체인 몬테 카를로(MCMC)를 사용하여 정확한 추론을 할 수 있습니다.
Pyro에서 사용할 알고리듬은 해밀턴 몬테카를로(HMC)를 효율적으로 자동 실행하는 방법을 제공하는 NUTS(No-U Turn Sampler)라고 합니다.
변동 추론(Variational Inference)보다 약간 느리지만 정확한 추정치를 제공합니다.
HMC (Hamiltonian Monte Carlo) 알아보기
잠깐 HMC에 대해서 알아보면 다음과 같습니다.
HMC는 일단 MCMC 방법 중 하나이고, Metropolis Hastings 알고리즘에 약간의 물리학 개념이 합쳐진 거로 이해하면 된다고 합니다.
Hamiltonian Dynamics을 활용하여, 보다 효율적으로 공간을 탐색하여 샘플링을 하는 것이 이 알고리즘의 핵심
HMC는, 연속되는 두 샘플 간의 correlation을 효과적으로 줄임으로써 MH 알고리즘에서 제안한 Gaussian Random Walk보다 더 효율적이고 빠르게 수렴
더 궁금하신 분은 이 글을 보시기를...
https://seunghan96.github.io/ml/stat/HMC/
NUTS (No-U-Turn Sampler) 알아보기
알아보려고 이것저것 뒤져봤는데, 지식이 부족해서 딱 이거다라는 설명을 못 찾았다
그냥 효과만 이야기하면, 기존에 랜덤으로 가는 것에 대한 특정 제약을 추가해서 다시 돌아오지 못하게 한다는 것인데,
이 그림을 완벽히 이해를 못 했지만... 샘플링을 할 때 기존에 선택된 공간으로 돌아가지 않고 계속 잘 샘플링해주는 것까지로 이해했다.(틀릴 수 있음. 아마 틀렸을 거임)

코드
from pyro.infer import MCMC, NUTS
nuts_kernel = NUTS(model)
mcmc = MCMC(nuts_kernel, num_samples=1000, warmup_steps=200)
mcmc.run(is_cont_africa, ruggedness, log_gdp)
hmc_samples = {k: v.detach().cpu().numpy() for k, v in mcmc.get_samples().items()}
for site, values in summary(hmc_samples).items():
print("Site: {}".format(site))
print(values, "\n")더 정확하게 뽑으니, 아까보다 편차가 더 늘어난 것을 알 수 있다.
Sample: 100%|██████████| 1200/1200 [00:34, 34.52it/s, step size=2.91e-01, acc. prob=0.938]
Site: a
mean std 5% 25% 50% 75% 95%
0 9.17485 0.137657 8.946845 9.084648 9.173862 9.266042 9.411255
Site: bA
mean std 5% 25% 50% 75% 95%
0 -1.824094 0.235498 -2.234271 -1.974982 -1.815298 -1.655515 -1.476725
Site: bAR
mean std 5% 25% 50% 75% 95%
0 0.337436 0.135221 0.120893 0.242686 0.332496 0.426281 0.561856
Site: bR
mean std 5% 25% 50% 75% 95%
0 -0.181102 0.078416 -0.315936 -0.232455 -0.183577 -0.127658 -0.051377
Site: sigma
mean std 5% 25% 50% 75% 95%
0 0.951507 0.052306 0.870548 0.918059 0.94928 0.983222 1.03996사후 분포 비교
변동 추론을 통해 얻은 잠재 변수의 사후 분포를 해밀턴 몬테 카를로의 분포와 비교해보겠습니다.
아래에서 볼 수 있듯이, 변동 추론의 경우, 다른 회귀 계수의 한계 분포는 (HMC에서) 실제 후방 w.r.t.로 과소 분산됩니다. 이것은 변동 추론에 의해 최소화되는 KL(q||p) 손실(진짜 후방과 근사 후방의 KL 발산)의 인공물입니다.
sites = ["a", "bA", "bR", "bAR", "sigma"]
fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 10))
fig.suptitle("Marginal Posterior density - Regression Coefficients", fontsize=16)
for i, ax in enumerate(axs.reshape(-1)):
site = sites[i]
sns.distplot(svi_samples[site], ax=ax, label="SVI (DiagNormal)")
sns.distplot(hmc_samples[site], ax=ax, label="HMC")
ax.set_title(site)
handles, labels = ax.get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right');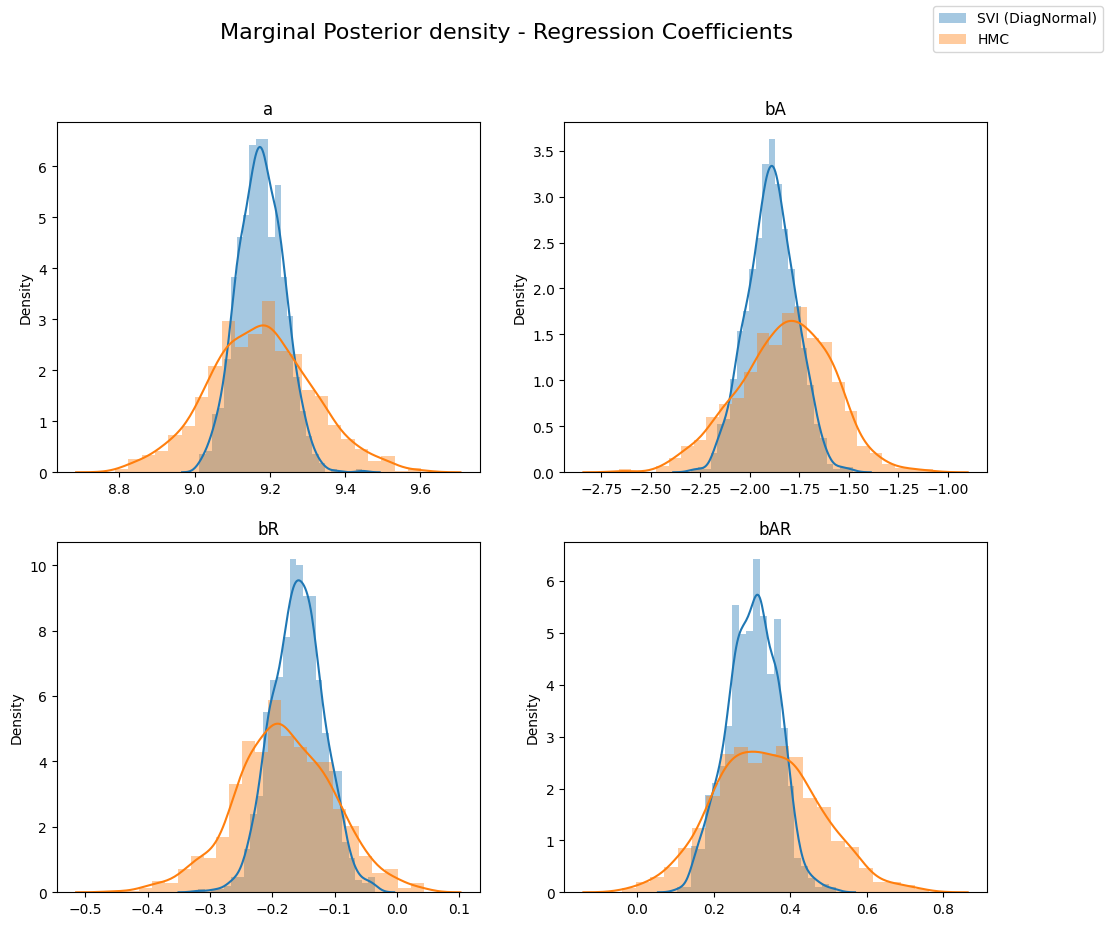
이것은 변동 추론의 대략적인 사후 분포와 중첩된 joint 사후 분포로부터 다른 단면을 그릴 때 더 잘 보일 수 있습니다.
변동 계열(variational famility)은 대각선 공분산을 가지고 있기 때문에 latents과 결과 근사치 사이의 상관관계를 모형화할 수 없습니다.
SVI로 추정한 분포는 대각선 공분산을 가정하기 때문에 동그란 형태를 띠고 있지만 HMC는 그런 가정이 없이 했기 때문에
공분 산성도 반영해서 나오다 보니 편차가 생긴 것을 알 수 있다.

MultivariateNormal Guide
위의 대각선 공분산 가이드를 사용하지 않고 이번에는 다변량 정규 분포 예시를 해보고자 합니다.
이전에 대각 정규 분포 가이드에서 얻은 결과와 비교하여 이제 다변량 정규 분포의 콜 레스키 인수분해로부터 샘플을 생성하는 가이드를 사용할 것입니다.
이를 통해 공분산 행렬을 통해 잠재 변수 간의 상관관계를 포착할 수 있습니다.
만약 이것을 수동으로 쓴다면, 우리는 Multivarite Normal Family를 공동으로 샘플링할 수 있도록 모든 잠재 변수를 결합해야 할 것입니다.
from pyro.infer.autoguide import AutoMultivariateNormal, init_to_mean
guide = AutoMultivariateNormal(model, init_loc_fn=init_to_mean)
svi = SVI(model,
guide,
optim.Adam({"lr": .01}),
loss=Trace_ELBO())
is_cont_africa, ruggedness, log_gdp = train[:, 0], train[:, 1], train[:, 2]
pyro.clear_param_store()
for i in range(num_iters):
elbo = svi.step(is_cont_africa, ruggedness, log_gdp)
if i % 500 == 0:
logging.info("Elbo loss: {}".format(elbo))Elbo loss: 691.7696694731712
Elbo loss: 420.9812924861908
Elbo loss: 248.2071254849434
Elbo loss: 248.8848677277565
Elbo loss: 247.06930607557297
Elbo loss: 247.4481406211853
Elbo loss: 247.9400673508644
Elbo loss: 247.89774000644684
Elbo loss: 247.7914559841156
Elbo loss: 248.32894295454025결과 그림 비교(HMC , MultivariateNormal Guide, Diagonal Normal Guide )
MultivariateNormal Guide와 HMC 비교
다시 사후 분포의 형태를 살펴보자. 다변수 가이드가 실제 사후 분포를 더 많이 확보할 수 있음을 알 수 있습니다.
predictive = Predictive(model, guide=guide, num_samples=num_samples)
svi_mvn_samples = {k: v.reshape(num_samples).detach().cpu().numpy()
for k, v in predictive(log_gdp, is_cont_africa, ruggedness).items()
if k != "obs"}
fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 10))
fig.suptitle("Marginal Posterior density - Regression Coefficients", fontsize=16)
for i, ax in enumerate(axs.reshape(-1)):
site = sites[i]
sns.distplot(svi_mvn_samples[site], ax=ax, label="SVI (Multivariate Normal)")
sns.distplot(hmc_samples[site], ax=ax, label="HMC")
ax.set_title(site)
handles, labels = ax.get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right');
MultivariateNormal Guide 와 Diagonal Normal Guide 비교
이제 Diagonal Normal 가이드와 Multivariate Normal 가이드에 의해 계산된 사후 값을 비교해 보겠습니다. 다변량 분포는 대각 정규분포보다 더 분산되어 있습니다.
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))
fig.suptitle("Cross-sections of the Posterior Distribution", fontsize=16)
sns.kdeplot(svi_samples["bA"], svi_samples["bR"], ax=axs[0], label="SVI (Diagonal Normal)")
sns.kdeplot(svi_mvn_samples["bA"], svi_mvn_samples["bR"], ax=axs[0], shade=True, label="SVI (Multivariate Normal)")
axs[0].set(xlabel="bA", ylabel="bR", xlim=(-2.5, -1.2), ylim=(-0.5, 0.1))
sns.kdeplot(svi_samples["bR"], svi_samples["bAR"], ax=axs[1], label="SVI (Diagonal Normal)")
sns.kdeplot(svi_mvn_samples["bR"], svi_mvn_samples["bAR"], ax=axs[1], shade=True, label="SVI (Multivariate Normal)")
axs[1].set(xlabel="bR", ylabel="bAR", xlim=(-0.45, 0.05), ylim=(-0.15, 0.8))
handles, labels = axs[1].get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right');
MultivariateNormal Guide와 HMC 비교 (2D)
HMC에서 계산한 사후 값이 있는 다변량 가이드. Multivariate 가이드는 실제 후방을 더 잘 포착합니다.
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))
fig.suptitle("Cross-sections of the Posterior Distribution", fontsize=16)
sns.kdeplot(hmc_samples["bA"], hmc_samples["bR"], ax=axs[0], shade=True, label="HMC")
sns.kdeplot(svi_mvn_samples["bA"], svi_mvn_samples["bR"], ax=axs[0], label="SVI (Multivariate Normal)")
axs[0].set(xlabel="bA", ylabel="bR", xlim=(-2.5, -1.2), ylim=(-0.5, 0.1))
sns.kdeplot(hmc_samples["bR"], hmc_samples["bAR"], ax=axs[1], shade=True, label="HMC")
sns.kdeplot(svi_mvn_samples["bR"], svi_mvn_samples["bAR"], ax=axs[1], label="SVI (Multivariate Normal)")
axs[1].set(xlabel="bR", ylabel="bAR", xlim=(-0.45, 0.05), ylim=(-0.15, 0.8))
handles, labels = axs[1].get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right');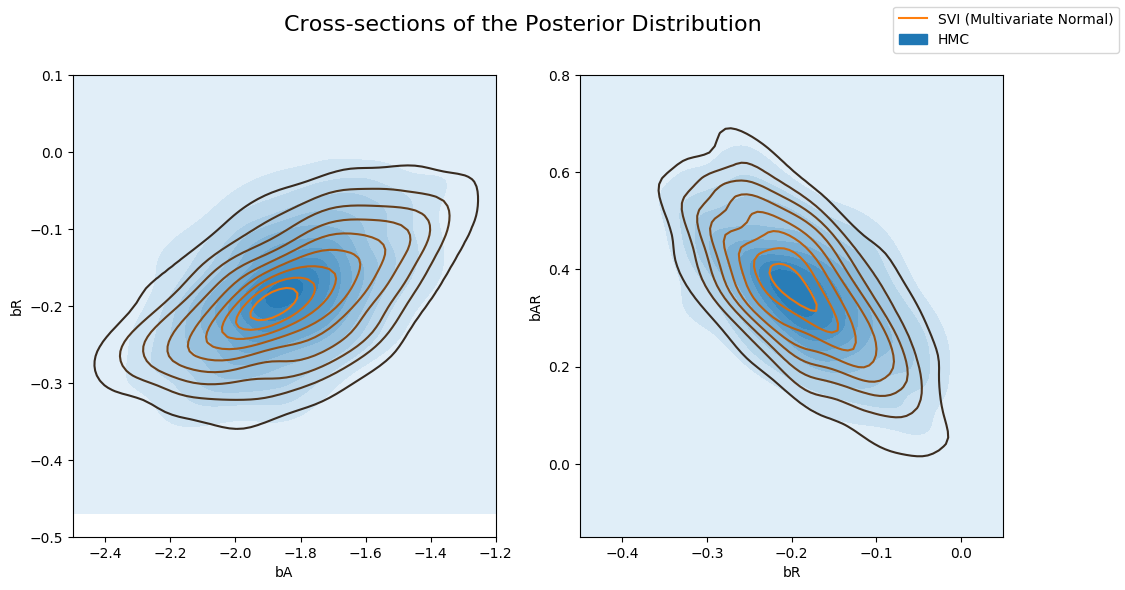
정리
베이지안을 하기 위해서는 분포를 가정해야 하고, 여기서는 사전 지식이 없다 보니, 노말 분포로만 가정을 하였지만, 이러한 분포 가정도 중요해 보인다.
그리고 샘플링을 하기 위해서는 SVI로 할 수도 있지만, 정확하게 뽑아내는 방법들이 있는데, 이 방법들은 역시 오랜 시간이 걸리기 때문에 개인적으로 SVI로 먼저 하고 먼가 더 유의미한 것을 뽑아낼 수 있을 때 HMC를 해보면 좋을 것 같다.
그렇지만 샘플이 적은 경우에는 이러한 방식이 딥러닝보다 좋아 보인다고는 생각도 들었다.
Reference
https://www.slideshare.net/xianblog/hmc-bi-p
https://seunghan96.github.io/ml/stat/HMC/
'분석 Python > Pyro' 카테고리의 다른 글
| [Pyro] Application - 5. GP Bayesian Optimization (0) | 2022.08.29 |
|---|---|
| [Pyro] Application - 4. Gaussian Process Latent Variable Model(GPLVM) (0) | 2022.08.29 |
| [Pyro] Application - 3. Gaussian Process 이해하기 (0) | 2022.08.28 |
| [Pyro] Application - 1. Bayesian Regression 이해하기 (1) | 2022.08.21 |
| [Pyro] 개념 파악 및 실습으로 알아보기 (1) | 2022.08.20 |