요즘 점점 결과가 나올 때 결과에 대한 불확실성에 대한 설명을 많이 필요로 한다는 것을 느끼고 있다.
기존 방식을 사용하면, 근사적으로라도 불확실성을 측정하는 수단(DROPOUT, 등등)이 있는 것 같다.
이제 불확실성이라는 것이 중요한데, 이걸로 구현을 할 수도 있어야 하니, 많은 라이브러리 중에서 토치를 지금 주로 사용하고 있으니 Pyro라는 것으로 사용하고 예제를 보면서, 이 쪽 부분을 이해하고자 한다.
미적분이 변화의 속도에 대한 추론을 위한 수학인 것처럼, 확률은 불확실성 하에서 추론의 수학이다. 그것은 현대 기계 학습과 AI의 많은 부분을 이해하기 위한 통일된 이론적 프레임워크를 제공한다.
확률 언어로 구축된 모델은 복잡한 추론을 포착하고, 모르는 것을 알고, 감독 없이 데이터에서 구조를 밝힐 수 있다.
확률론적 모델을 직접 지정하는 것은 번거로울 수 있으며 이를 구현하는 것은 오류가 발생하기 매우 쉽다.
확률론적 프로그래밍 언어(PPL)는 확률을 프로그래밍 언어의 표현력과 결합함으로써 이러한 문제를 해결한다.
확률론적 프로그램은 일반적인 결정론적 계산과 데이터의 생성 과정을 나타내는 무작위로 샘플링된 값의 혼합이다.
확률론적 프로그램의 결과를 관찰함으로써, 우리는 추론 문제를 설명할 수 있는데, 대략 다음과 같이 번역된다:
"만약 이 무작위 선택이 특정한 관측치를 가지고 있다면 무엇이 참이어야 하는가?"
PPL은 모델의 사양, 응답할 쿼리 및 해답을 계산하는 알고리즘 사이에서 확률 수학에 이미 내포된 우려를 명시적으로 분리한다.
파이로(Pyro)는 파이썬과 파이토치에 기반한 확률론적 프로그래밍 언어이다. 파이로 프로그램은 단지 파이썬 프로그램일 뿐인 반면, 주요 추론 기술은 추상적인 확률론적 계산을 파이토치의 확률적 기울기 강하로 해결된 구체적인 최적화 문제로 변환하여 확률론적 방법을 이전에 다루기 어려운 모델과 데이터 세트 크기에 적용할 수 있게 한다.
대부분 이 글에서는 튜토리얼을 따라가면서 공부하면서, 추가적으로 다른 글들도 참고해보면서 확률적인 개념과 그 개념을 실제로 구현을 어떻게 쓰는 지를 알아보고자 한다.
Background: probabilistic machine learning
대부분의 데이터 분석 문제는 다음과 같은 세 가지 기본적인 고급 질문에 대한 정교함으로 이해할 수 있다.
1. 데이터를 관찰하기 전에 문제에 대해 무엇을 알고 있습니까?
2. 사전 지식을 바탕으로 데이터에서 어떤 결론을 도출할 수 있는가?
3. 이 결론들이 말이 됩니까?
데이터 과학과 기계 학습에 대한 확률론적 또는 베이지안 접근 방식에서, 우리는 확률 분포에 대한 수학적 연산 측면에서 이를 공식화한다.
Background: probabilistic models¶
첫째로, 우리는 문제의 변수와 변수 사이의 관계에 대해 알고 있는 모든 것을 확률적 모델 또는 무작위 변수 집합에 대한 공동 확률 분포의 형태로 표현한다.
즉 우리가 아는 변수들이 어떤 분포를 가지고 있다는 가정을 한다고 생각하면 될 것 같다.

모델은 관측 x를 가지고 있고, 그 x에는 z 라고 하는 latent random variable이 있다고 한다.
조인트 확률 함수는 다음고 같이 나올 수 있고, 여기서 p(z)는 사전(prior)이라하고, p(x|z)는 우도(likelihood)라고 한다.
Pyro에서는 일반적으로 모델을 구성하는 다양한 조건부 확률 분포가 다음과 같은 특성(일반적으로 Pyro 및 PyTorch 분포에서 사용 가능한 분포로 만족함)을 가질 것을 요구한다.

확률론적 모델은 종종 시각화 및 통신을 위한 표준 그래픽 표기법으로 묘사됨.
Pyro에서는 고정된 그래픽 구조를 가지지 않는 모델을 나타낼 수 있다.
반복이 많은 모델에서는 내부에 있는 랜덤 변수의 여러 독립적인 사본을 나타내기 위해 변수 주변의 직사각형 "Plate"로 그래픽으로 표시되기 때문에 Plate(플레이트) 표기법을 사용하는 것이 편리하다.
Inference
일단 모델을 지정하면, 베이즈의 규칙은 다음과 같은 사후 분포를 계산하여 추론을 수행하거나 데이터에서 잠재 변수에 대한 결론을 도출하기 위해 그것을 사용하는 방법을 알려준다.
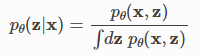
모델링 및 추론 결과를 확인하기 위해, 우리는 모형이 관측된 데이터에 얼마나 잘 맞는지 알고 싶다.
이는 증거(evidence) 또는 marginal likelihood를 사용하여 정량화할 수 있다.

새로운 데이터에 예측을 하기 위해서 posterir predictive distribution을 만들 수 있다.

마지막으로, 관찰된 데이터에서 모델의 매개 변수를 배우는 것이 종종 바람직하며, 이는 marginal likelihood을 최대화하여 수행할 수 있다.
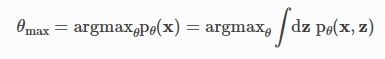
Inference in Pyro
Background: variational inference
도입부에서 각각의 계산(사후 분포, 한계 가능성 및 사후 예측 분포)은 종종 불가능하거나 계산적으로 다루기 힘든 적분을 수행해야 합니다.
Pyro는 많은 다른 정확하고 근사적인 추론 알고리듬에 대한 지원을 포함하지만, 가장 잘 지원되는 변형 추론(variatioinal inference)은 다루기 어려운 적분을 와의 함수의 최적화로 변환하여 실제 알려지지 않은 후면에 대한 다루기 쉬운 근사치를 찾고 계산하는 통일된 체계를 제공한다.
아래 그림은 이 과정을 개념적으로 묘사한 반면 SVI 튜토리얼에서는 보다 포괄적인 수학적 소개를 이용할 수 있다.

대부분의 확률 분포(아래 그림의 밝은 타원)는 직접 표현하기에는 너무 복잡하기 때문에, 우리는 실제 값 매개 변수에 의해 색인화된 분포의 더 작은 부분 공간을 정의해야 한다.
(위의 그림에서) 그러나 실제 사후 분포(아래 그림에서 빨간색 별)는 포함되지 않을 수 있다.
variational inference은 거리 또는 발산(divergence)(위의 그림의 검은 화살표)에 따라 실제 사후(아래 그림의 노란색 별)과 가장 유사한 것을 찾기 위해 변이적 분포 공간을 탐색함으로써 실제 후방과 근사한다.
그러나 확률 분포 간의 거리 또는 차이를 측정하는 방법은 여러 가지가 있습니다.
어떤 걸로 할까요? 그림에서 알 수 있듯이, 이론적으로 매력적인 선택은 쿨백-라이블러 발산이지만, 이것을 직접 계산하려면 실제 사후 분포을 미리 알아야 하기 때문에 목적을 달성할 수 없다.
즉, KL-Divergence는 쓰기 어렵다.
더욱이, 우리는 이 분기를 최적화하는 데 관심이 있는데, 이는 훨씬 더 어렵게 들릴 수 있지만, 실제로 베이즈의 정리를 사용하여 의 정의를 의존하지 않는 다루기 어려운 상수와 아래에 정의된 증거 하한(ELBO)이라고 불리는 다루기 쉬운 용어 사이의 차이로 다시 쓰는 것이 가능하다.
따라서 이 다루기 쉬운 항을 최대화하면 원래의 KL-발산을 최소화하는 것과 동일한 솔루션이 생성될 것이다.
Background: “guide” programs as flexible approximate posteriors
변분 추론(variational inference)에서, 우리는 변형 매개 변수라고 알려진 실제 사후 분포와 근사하기 위해 매개 변수화된 분포를 도입한다.
이 분포는 많은 문헌에서 variational distribution라고 불리며, Pyro의 맥락에서는 guide라고 불린다.
variational distribution == guide(Pyro)
모델과 마찬가지로 guide는 pyro.sample 및 pyro.param 문을 포함하는 파이썬 프로그램 가이드()로 인코딩된다.
guide는 표본 추출이 용이하도록 정규화된 분포여야 하므로 관측된 데이터가 포함되어 있지 않습니다.
Pyro에서는 model()과 guide()가 동일한 인수(same argument)를 사용해야 합니다.
guide가 임의의 Pyro 프로그램이 되도록 허용하면 아래 그림에 개략적으로 묘사된 것처럼 유용한 방향으로만 검색 공간을 확장하여 실제 사후 분포 문제별 구조를 더 많이 포착하는 guide 패밀리를 작성할 가능성이 열린다.

변분 추론 수학에 의해 guide에 어떤 제한이 부과되는가?
guide는 사후에 대한 근사치이기 때문에 guide는 모델의 모든 잠재 랜덤 변수에 대해 유효한 관절 확률 밀도를 제공해야 한다.
랜덤 변수가 Pyro.sample()이라는 원시 문장으로 Pyro에 지정되면 첫 번째 인수가 랜덤 변수의 이름을 나타냅니다. 이러한 이름은 모형 및 가이드의 랜덤 변수를 정렬하는 데 사용됩니다. 모형이 랜덤 변수 z_1을 포함하는 경우, 매우 명백하다.
model과 guide 동일하게 작성한다.
def model():
pyro.sample("z_1", ...)
def guide():
pyro.sample("z_1", ...)
두 경우에 사용되는 분포는 다를 수 있지만 이름은 1:1로 정렬되어야 합니다.
유연성에도 불구하고 가이드를 손으로 작성하는 것은 특히 신규 사용자에게 어렵고 지루할 수 있다. 가능할 때마다 자동 가이드를 사용하거나 Pyroin.infer와 함께 제공되는 모델에서 공통 가이드 패밀리를 자동으로 생성하는 방법을 사용하는 것이 좋습니다.pyro.infer.autoguide.의 다음 섹션에서는 두 가지 접근 방식을 모두 시연합니다.
auto_guide = pyro.infer.autoguide.AutoNormal(model)Example: Geography and national income
해당 예제에서는 Terrain Ruggedness Index(데이터 세트의 험한 변수)로 측정한 국가의 지형 이질성( tepographic heterogeneity)과 1인당 GDP 사이의 관계를 탐구하고자 합니다.
특히 원본 논문의 저자들에 의해 주목되었다. ("Ruggedness: 아프리카에서의 나쁜 지리의 축복)은 지형의 험준함이나 나쁜 지리는 아프리카 밖의 경제 실적과 관련이 있지만, 험준한 지형은 아프리카 국가들의 소득에 역효과를 가져왔다.
- rugged: quantifies the Terrain Ruggedness Index;
- cont_africa: whether the given nation is in Africa;
- rgdppc_2000: Real GDP per capita for the year 2000;
DATA_URL = "https://d2hg8soec8ck9v.cloudfront.net/datasets/rugged_data.csv"
data = pd.read_csv(DATA_URL, encoding="ISO-8859-1")
df = data[["cont_africa", "rugged", "rgdppc_2000"]]
df = df[np.isfinite(df.rgdppc_2000)]
## skew하기 때문에 로그 변환
df["rgdppc_2000"] = np.log(df["rgdppc_2000"])
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 6), sharey=True)
african_nations = df[df["cont_africa"] == 1]
non_african_nations = df[df["cont_africa"] == 0]
sns.scatterplot(x=non_african_nations["rugged"],
y=non_african_nations["rgdppc_2000"],
ax=ax[0])
ax[0].set(xlabel="Terrain Ruggedness Index",
ylabel="log GDP (2000)",
title="Non African Nations")
sns.scatterplot(x=african_nations["rugged"],
y=african_nations["rgdppc_2000"],
ax=ax[1])
ax[1].set(xlabel="Terrain Ruggedness Index",
ylabel="log GDP (2000)",
title="African Nations");
위에서 한 가설처럼 실제로 데이터상에서 보게 되면 데이터를 시각화하면 견고성과 GDP 사이에 실제로 가능한 관계가 있음을 알 수 있지만 이를 확인하려면 추가 분석이 필요합니다.
베이지안 선형 회귀를 통해 Pyro에서 이 작업을 수행하는 방법을 볼 것입니다.
Pyro의 확률론적 모델은 수행되는 높은 수준의 계산에 따라 Pyro의 내부로 동작이 변경될 수 있는 특수 원시 함수를 사용하여 잠재 변수에서 관측된 데이터를 생성하는 Python 함수 모델(*args, **kwargs)로 지정됩니다.
특히, 모델()의 다른 수학적 조각들은 매핑을 통해 인코딩된다:

Example model: Maximum-likelihood linear regression
선형 회귀 예측자 βX+α에 대한 공식을 Python 표현식으로 작성하면 다음을 얻습니다.
mean = a + b_a * is_cont_africa + b_r * ruggedness + b_ar * is_cont_africa * ruggedness이를 데이터 세트에 대한 완전한 확률론적 모델로 구축하려면, 회귀 계수와 학습 가능한 매개 변수를 만들고 예측 평균 주위에 관측 노이즈를 추가해야 한다.
우리는 위에 소개된 Pyro primitives를 사용하여 이를 표현하고 fyro.render_model()을 사용하여 결과 모델을 시각화할 수 있다.
그래서 위에 했던 식을 Pyro에서 모델링 하면 다음과 같다.
즉 학습하고자 하는 파라미터들에 대해서 정의를 하고 원하면 제한 조건도 걸 수 있다.
위에서 선형 회귀를 가정하고, 그것을 노말이라는 분포를 가정에서 plate를 구성하였다.
import pyro.distributions as dist
import pyro.distributions.constraints as constraints
def simple_model(is_cont_africa, ruggedness, log_gdp=None):
a = pyro.param("a", lambda: torch.randn(()))
b_a = pyro.param("bA", lambda: torch.randn(()))
b_r = pyro.param("bR", lambda: torch.randn(()))
b_ar = pyro.param("bAR", lambda: torch.randn(()))
sigma = pyro.param("sigma", lambda: torch.ones(()), constraint=constraints.positive)
mean = a + b_a * is_cont_africa + b_r * ruggedness + b_ar * is_cont_africa * ruggedness
with pyro.plate("data", len(ruggedness)):
return pyro.sample("obs", dist.Normal(mean, sigma), obs=log_gdp)
pyro.render_model(simple_model, model_args=(is_cont_africa, ruggedness, log_gdp), render_distributions=True)
plate 만 보여주면 obs는 결국 우리가 얻게 된 관측치(타겟)을 기반으로 모델링되게 된다.
pyro.render_model(simple_model, model_args=(is_cont_africa, ruggedness, log_gdp), render_distributions=True, render_params=True)

디테일하게 파라미터까지 표현하면 다음과 같이 보여진다.
Background: the pyro.sample primitive
Pyro의 확률 프로그램은 pyro.sample로 표시된 원시 확률 분포의 샘플을 중심으로 구축됩니다.
def sample(
name: str,
distribution: pyro.distributions.Distribution,
*,
obs: typing.Optional[torch.Tensor] = None,
infer: typing.Optional[dict] = None
) -> torch.Tensor:
...위의 코드에서는 다음과 같이 표현되었다.
sample에 이름을 넣고, 어떠한 분포를 넣을지 그리고 관측치는 무엇인지를 넣는다.
return pyro.sample("obs", dist.Normal(mean, sigma), obs=log_gdp)위의 코드는 simple_model에 log_gdp 값이 주어지는지에 따라 잠재 변수 또는 관측 변수를 나타낼 수 있다.
log_gdp가 제공되지 않고 "obs"가 잠재되어 있을 때, 이는 분포의 기초가 되는 .sample 방법을 호출하는 것과 동등하다.
return dist.Normal(mean, sigma).sample()이 해석은 Pyro 프로그램을 확률적 함수로 언급하는 경우가 있는데, 이는 일부 Pyro의 이전 문서에서 사용된 다소 모호한 용어입니다.
Example: from maximum-likelihood regression to Bayesian regression
선형 회귀 모델을 베이지안(Bayesian)으로 만들려면 매개 변수와 (여기서 스칼라 b_a, b_r 및 b_ar로 확장)에 대한 사전 분포를 지정해야 합니다. 이 분포에 대한 합리적인 값에 대한 데이터를 관찰하기 전에 우리의 믿음(beliefs)을 나타내는 확률 분포입니다. 또한 관측 노이즈를 제어하는 랜덤 스케일 매개 변수도 추가할 것입니다.
Pyro에서 베이지안 모델을 표현하는 직관적이라고 이야기 하는데, pyro.param을 pyro.sample로만 바꾸면 된다고 합니다.
상수텀에 대해서는 GDP에 대한 베이스라인 지식의 부족을 표현하기 위해서 큰 편차를 가지게하는 노말 사전 분포를 사용했다.
회귀 계수들은 변수와 GDP사이의 관계가 양수인지 음수인지 모르기 떄문에 0을 중심으로 했다.
sigma는 항상 0보다 커야하기 때문에 uniform으로 했다.
def model(is_cont_africa, ruggedness, log_gdp=None):
a = pyro.sample("a", dist.Normal(0., 10.))
b_a = pyro.sample("bA", dist.Normal(0., 1.))
b_r = pyro.sample("bR", dist.Normal(0., 1.))
b_ar = pyro.sample("bAR", dist.Normal(0., 1.))
sigma = pyro.sample("sigma", dist.Uniform(0., 10.))
mean = a + b_a * is_cont_africa + b_r * ruggedness + b_ar * is_cont_africa * ruggedness
with pyro.plate("data", len(ruggedness)):
return pyro.sample("obs", dist.Normal(mean, sigma), obs=log_gdp)
pyro.render_model(model, model_args=(is_cont_africa, ruggedness, log_gdp), render_distributions=True)
Example: mean-field variational approximation for Bayesian linear regression in Pyro
베이지안 선형 회귀의 실행 예시로, 모델에서 관찰되지 않은 매개 변수의 분포를 대각선 공분산을 가진 가우스(즉, 잠재 변수 사이에 상관관계가 없다고 가정함)로 모델링하는 가이드를 사용할 것이다. 이것은 평균장 근사치라고 알려져 있는데, 이는 원래 이러한 근사치가 발명된 물리학에서 차용한 용어이다.
Pyro는 pyro.render_model을 사용하여 custom_guide를 시각화할 수 있으며, 이는 무작위 변수 사이에 가장자리가 없는 것으로 표시되는 것처럼 무작위 변수가 실제로 서로 독립적임을 보여줍니다.
def custom_guide(is_cont_africa, ruggedness, log_gdp=None):
a_loc = pyro.param('a_loc', lambda: torch.tensor(0.))
a_scale = pyro.param('a_scale', lambda: torch.tensor(1.),
constraint=constraints.positive)
sigma_loc = pyro.param('sigma_loc', lambda: torch.tensor(1.),
constraint=constraints.positive)
weights_loc = pyro.param('weights_loc', lambda: torch.randn(3))
weights_scale = pyro.param('weights_scale', lambda: torch.ones(3),
constraint=constraints.positive)
a = pyro.sample("a", dist.Normal(a_loc, a_scale))
b_a = pyro.sample("bA", dist.Normal(weights_loc[0], weights_scale[0]))
b_r = pyro.sample("bR", dist.Normal(weights_loc[1], weights_scale[1]))
b_ar = pyro.sample("bAR", dist.Normal(weights_loc[2], weights_scale[2]))
sigma = pyro.sample("sigma", dist.Normal(sigma_loc, torch.tensor(0.05)))
return {"a": a, "b_a": b_a, "b_r": b_r, "b_ar": b_ar, "sigma": sigma}
pyro.render_model(custom_guide, model_args=(is_cont_africa, ruggedness, log_gdp), render_params=True)
Pyro에는 또한 주어진 모델에서 가이드 프로그램을 자동으로 생성하는 광범위한 "자동 가이드" 컬렉션이 포함되어 있다. 우리 손으로 쓴 가이드처럼, 모두 Pyro.autoguide.AutoGuide 인스턴스(그 자체는 모델과 동일한 인수를 사용하는 함수)는 포함된 각 pyro.sample site에 대한 값 사전을 반환합니다.
가장 간단한 autoguide 클래스는 위에서 손으로 작성한 것과 동일한 한 줄의 코드로 가이드를 자동으로 생성하는 AutoNormal입니다.
auto_guide = pyro.infer.autoguide.AutoNormal(model)그러나 가이드만 추론 알고리즘을 완전히 명시하지는 않는다.
그것은 단지 매개 변수에 의해 색인화된 가능한 대략적인 사후 분포와 초기 매개 변수 값에 의해 결정되는 공간의 초기 점에 대한 검색 공간을 설명한다.
그런 다음 매개 변수(위 그림의 노란색 별)에 대한 최적화 문제를 해결하여 이 초기 분포를 진정한 사후 분포(위 그림의 빨간색 별)로 이동해야 합니다.
이 최적화 문제를 공식화하고 해결하는 것은 다음 두 절의 주제이다.
Background: Estimating and optimizing the Evidence Lower Bound (ELBO)

최적화할 모델 pθ(x,z) 및 가이드 qϕ(z)의 기능은 기대치 w.r.t로 정의되는 ELBO이다.
가정하면 기대치 내부의 모든 확률을 계산할 수 있고, 가이드가 표본 추출할 수 있는 매개 변수 분포로 가정되기 때문에 모델과 가이드 매개 변수에 대한 기울기뿐만 아니라 이 양의 몬테카를로 추정치를 계산할 수 있다.
이러한 기울기 추정을 사용하여 확률적 기울기 하강법을 통해 모델 및 가이드 매개변수 θ,ϕ에 대한 ELBO를 최적화하는 것을 확률적 변동 추론(SVI)이라고 합니다. SVI에 대한 확장된 소개는 SVI 파트 I을 참조하십시오.
Example: Bayesian regression via stochastic variational inference (SVI)
Pyro에는 ELBO(이전 섹션에서 수학적으로 정의됨)에 대한 여러 가지 다른 추정기 구현이 포함되어 있으며, 각 추정기는 서로 다른 트레이드오프로 손실과 기울기를 약간 다르게 계산한다.
이 튜토리얼에서는 pyro.infer만 사용
Trace_ELBO는 항상 정확하고 안전하게 실행할 수 있으며, 다른 ELBO 추정기는 특정 모델과 가이드에 계산 또는 통계적인 이점을 제공할 수 있다.
예시 모델에서 추론을 위해 SVI를 사용하여 Pyro.infer의 출력을 최적화하기 위해 PyroTorch의 확률적 경사 하강 구현을 어떻게 사용하는지를 보여줄 것이다.
pyro.infer에 전달하는 Trace_ELBO 개체입니다.
SVI는 step() 메서드가 손실 및 매개 변수 기울기를 계산하고 매개 변수에 업데이트 및 제약 조건을 적용하는 것을 담당하는 도우미 클래스입니다.
pyro.infer안에는 여러개가 있는데 그 중에서 정확하고 안전한 Trace_ELBO를 사용하여 기울기 경사 방법으로 학습
adam = pyro.optim.Adam({"lr": 0.02})
elbo = pyro.infer.Trace_ELBO()
svi = pyro.infer.SVI(model, auto_guide, adam, elbo)여기 pyro.optim.Adam은 PyTorch 옵티마이저 torch.optim 주위에 얇은 포장체입니다. Adam(토론하려면 여기를 참조하십시오).
pyro.optimizer의 Optimizer는 Pyro의 파라미터 저장소에서 파라미터 값을 최적화하고 업데이트하는 데 사용됩니다. 특히, 학습 가능한 매개 변수는 가이드 코드에 의해 결정되고 SVI 클래스 내 장면 뒤에서 자동으로 발생하기 때문에 최적기에 전달할 필요가 없습니다.
ELBO 그레이디언트 단계를 밟기 위해 우리는 단순히 SVI의 단계 방법이라고 부른다. SVI.step에 전달하는 데이터 인수는 model()과 guide()에 모두 전달됩니다. 전체 교육 루프는 다음과 같습니다.
%%time
pyro.clear_param_store()
# These should be reset each training loop.
auto_guide = pyro.infer.autoguide.AutoNormal(model)
adam = pyro.optim.Adam({"lr": 0.02}) # Consider decreasing learning rate.
elbo = pyro.infer.Trace_ELBO()
svi = pyro.infer.SVI(model, auto_guide, adam, elbo)
losses = []
for step in range(1000 if not smoke_test else 2): # Consider running for more steps.
loss = svi.step(is_cont_africa, ruggedness, log_gdp)
losses.append(loss)
if step % 100 == 0:
logging.info("Elbo loss: {}".format(loss))
plt.figure(figsize=(5, 2))
plt.plot(losses)
plt.xlabel("SVI step")
plt.ylabel("ELBO loss");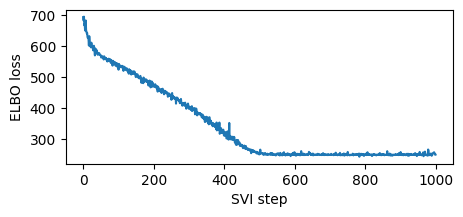
높은 학습률을 사용했기 때문에 이 교육은 빠릅니다. 때로는 모델이나 가이드가 학습률에 민감하게 반응하기도 하는데, 가장 먼저 시도해야 할 것은 학습률을 낮추고 단계를 늘리는 것이다.
(learning rate를 줄이고, step을 늘리기)
이것은 심층 신경망을 가진 모델과 가이드에서 특히 중요하다. 우리는 추론이 분기하거나 NAN을 초래할 수 있는 너무 빠른 학습 속도를 피하면서 낮은 학습률에서 시작하여 점차 증가하는 것을 추천한다.
for name, value in pyro.get_param_store().items():
print(name, pyro.param(name).data.cpu().numpy())
AutoNormal.locs.a 9.173145
AutoNormal.scales.a 0.0703669
AutoNormal.locs.bA -1.8474661
AutoNormal.scales.bA 0.1407009
AutoNormal.locs.bR -0.19032118
AutoNormal.scales.bR 0.044044234
AutoNormal.locs.bAR 0.35599768
AutoNormal.scales.bAR 0.079374395
AutoNormal.locs.sigma -2.205863
AutoNormal.scales.sigma 0.060526706
가이드를 교육한 후, 우리는 Pyro의 매개 변수 저장소에서 가져와 최적화된 가이드 매개 변수 값을 검사할 수 있다. 아래에 인쇄된 각 (위치, 척도) 쌍은 단일 파이로 분포를 모수화합니다.이전에 손으로 작성한 custom_guide와 유사한 모델의 관찰되지 않은 다른 pyro.sample 문장에 해당하는 가이드의 정규 분포입니다.
마지막으로, 지형 울퉁불퉁함과 GDP 사이의 관계가 우리 모델의 매개 변수 추정치의 불확실성에 대해 얼마나 견고한지에 대한 이전의 질문을 다시 살펴보자. 이를 위해 아프리카 안팎의 국가에 대한 지형 울퉁불퉁함을 고려한 로그 GDP의 기울기 분포를 그린다.
우리는 훈련된 가이드에서 추출한 샘플로 이 두 가지 분포를 나타낸다. 여러 샘플을 병렬로 그리기 위해, 우리는 pyro.plate 문 내에서 가이드를 호출할 수 있는데, 이는 pyro.plate 프리미티브를 소개하는 섹션에 설명된 대로 가이드의 각 pyro.sample 문에 대한 샘플링 작업을 반복하고 벡터화한다.
아래에서 볼 수 있듯이, 아프리카 국가들의 확률 질량은 대체로 양의 지역에 집중되어 있고 다른 국가들의 확률 질량은 원래의 가설에 더욱 신빙성을 부여한다.
그러나 비아프리카 국가의 사후 불확실성(주황색 히스토그램의 너비)은 아프리카 국가(파란색 히스토그램의 너비)보다 상당히 낮게 나타나는데, 원본 데이터의 유사한 범위를 고려할 때 놀라운 일이다. 이 불일치는 다음 섹션에서 더 자세히 조사할 것입니다.
fig = plt.figure(figsize=(10, 6))
sns.histplot(gamma_within_africa.detach().cpu().numpy(), kde=True, stat="density", label="African nations")
sns.histplot(gamma_outside_africa.detach().cpu().numpy(), kde=True, stat="density", label="Non-African nations", color="orange")
fig.suptitle("Density of Slope : log(GDP) vs. Terrain Ruggedness");
plt.xlabel("Slope of regression line")
plt.legend()
plt.show()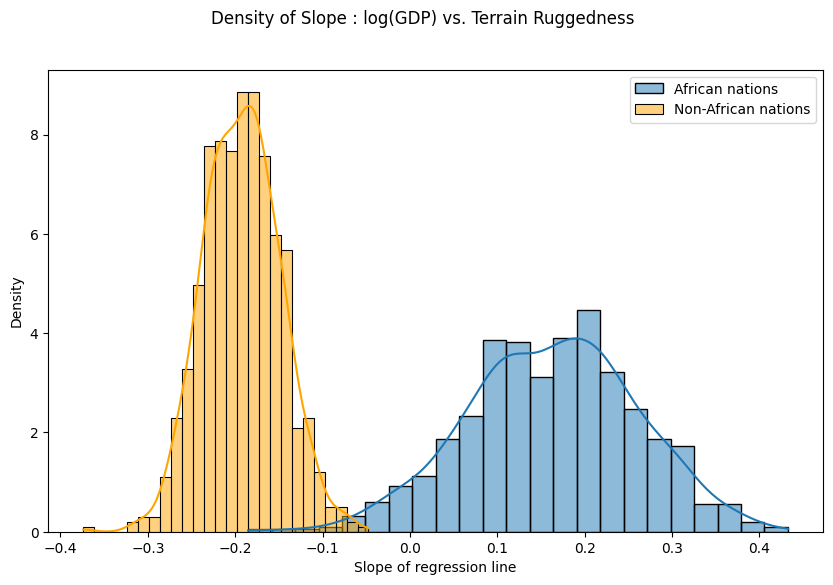
Model Evaluation in Pyro
Background: Bayesian model evaluation with posterior predictive checks
우리의 추론 결과를 신뢰할 수 있는지 여부를 평가하기 위해, 우리는 우리 모델에 의해 유도된 가능한 새로운 데이터에 대한 사후 예측 분포를 기존의 관찰된 데이터와 비교할 것이다. 이 분포를 계산하는 것은 실제 사후를 아는 것에 의존하기 때문에 일반적으로 다루기 어렵지만, 우리는 변분 추론에서 얻은 근사 후방을 사용하여 쉽게 근사할 수 있다.
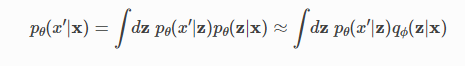
구체적으로, 사후 예측으로부터 대략적인 표본을 추출하기 위해, 우리는 단순히 표본을 추출한다.
대략적인 사후 분포에서, 그리고 나서 우리가 이전을 우리의 (대략적인) 후방으로 대체한 것처럼, 그 샘플이 주어진 모델에서 관찰된 변수에 대한 분포로부터 샘플.
Example: posterior predictive uncertainty in Pyro
선형 회귀 모델을 우리의 예제에서 표현하기 위해서는, 사후 예측 분포로부터 몇 개의 샘플을 추출하여 시각화해야 한다.
학습된 모델을 바탕으로 800개 샘플을 생성시켰다고 한다.
내부적으로, 이것은 먼저 가이드에서 잠재 변수에 대한 샘플을 생성한 다음 관찰되지 않은 pyro.sample 문에 의해 반환된 값을 가이드에서 샘플링된 해당 값으로 변경하면서 모델을 전진 실행함으로써 수행된다.
아래 그림은 베이지안을 적용했을 때 90의 credible interval을 받게 됬습니다.
두 가지 근사치에서 비아프리카 국가에 대한 사후 예측 분포의 90% 신뢰 구간을 시각화하여 관찰된 데이터의 적용 범위가 다소 향상되었음을 확인합니다.
predictions = pd.DataFrame({
"cont_africa": is_cont_africa,
"rugged": ruggedness,
"y_mean": svi_gdp.mean(0).detach().cpu().numpy(),
"y_perc_5": svi_gdp.kthvalue(int(len(svi_gdp) * 0.05), dim=0)[0].detach().cpu().numpy(),
"y_perc_95": svi_gdp.kthvalue(int(len(svi_gdp) * 0.95), dim=0)[0].detach().cpu().numpy(),
"true_gdp": log_gdp,
})
african_nations = predictions[predictions["cont_africa"] == 1].sort_values(by=["rugged"])
non_african_nations = predictions[predictions["cont_africa"] == 0].sort_values(by=["rugged"])
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 6), sharey=True)
fig.suptitle("Posterior predictive distribution with 90% CI", fontsize=16)
ax[0].plot(non_african_nations["rugged"], non_african_nations["y_mean"])
ax[0].fill_between(non_african_nations["rugged"], non_african_nations["y_perc_5"], non_african_nations["y_perc_95"], alpha=0.5)
ax[0].plot(non_african_nations["rugged"], non_african_nations["true_gdp"], "o")
ax[0].set(xlabel="Terrain Ruggedness Index", ylabel="log GDP (2000)", title="Non African Nations")
ax[1].plot(african_nations["rugged"], african_nations["y_mean"])
ax[1].fill_between(african_nations["rugged"], african_nations["y_perc_5"], african_nations["y_perc_95"], alpha=0.5)
ax[1].plot(african_nations["rugged"], african_nations["true_gdp"], "o")
ax[1].set(xlabel="Terrain Ruggedness Index", ylabel="log GDP (2000)", title="African Nations");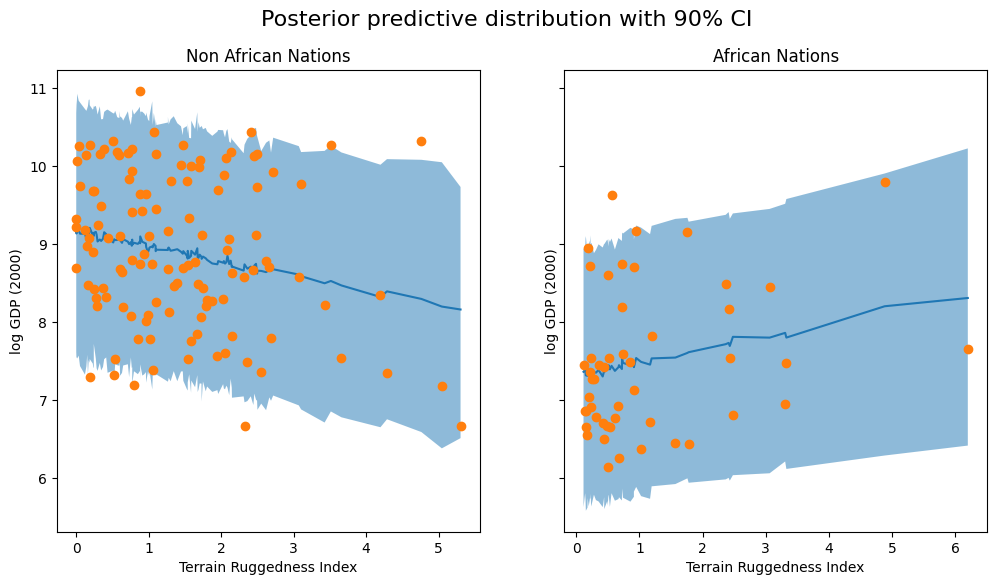
정리
일단 Pyro에 대해서 간단하게 이해를 해보자면 학습하고자 하는 파라미터에 대한 정의를 해야하고(pyro.param, pyro.sample),
그리고 그것에 대한 식을 또 정의를 해서 우리가 비교하고자 하는 obs에 분포라고 가정하는 것이 plate
그리고 이렇게 가정한 것과 실제 관측치와 특정 분포와의 거리를 가깝게 하기 위해서 경사 하강 방법을 사용하고, 메트릭으로는 elbo와 같은 것을 사용
이때 stochastic variational inference(svi) 에 step을 사용하여 파라미터를 학습하게 된다.
그렇게 하면 각 예측치에 대한 불확실성까지 반영하면서 결과를 얻을 수 있게 된다.
'분석 Python > Pyro' 카테고리의 다른 글
| [Pyro] Application - 5. GP Bayesian Optimization (0) | 2022.08.29 |
|---|---|
| [Pyro] Application - 4. Gaussian Process Latent Variable Model(GPLVM) (0) | 2022.08.29 |
| [Pyro] Application - 3. Gaussian Process 이해하기 (0) | 2022.08.28 |
| [Pyro] Application - 2. Bayesian Regression 이해하기 2 (0) | 2022.08.28 |
| [Pyro] Application - 1. Bayesian Regression 이해하기 (1) | 2022.08.21 |