지난번에 문서를 보면서, 베이지안 학습 방식에 대한 개념과 Pyro 사용법에 대해서 알게 되었지만,
아직 실제로 이러한 방법을 현실에 어떻게 쓰는지 와닿지 않기 때문에 예제와 함께 알아보고자 한다.
이번에는 베이지안 회귀분석 예제를 보고 이해해보고자 한다.
참고 자료
2022.08.21 - [분석 Python/Pyro] - [Pyro] Application - 1. Bayesian Regression 이해하기
2022.08.28 - [분석 Python/Pyro] - [Pyro] Application - 2. Bayesian Regression 이해하기 2
2022.08.28 - [분석 Python/Pyro] - [Pyro] Application - 3. Gaussian Process 이해하기
2022.08.29 - [분석 Python/Pyro] - [Pyro] Application - 5. GP Bayesian Optimization
Bayesian Regression
회귀는 기계 학습에서 가장 일반적이고 기본적인 지도 학습 작업 중 하나이다.
아래 그림처럼 회귀분석을 할 때는 데이터셋으로부터 x, y를 정의하고, x를 이용해서 y를 잘 적합시키는 w와 b를 찾아야 한다.

이 튜토리얼에서는 먼저 PyTorch에서 선형 회귀 분석을 구현하고 파라미터 및 에 대한 포인트 추정치를 학습한다.
그런 다음 Pyro를 사용하여 베이지안 회귀 분석을 구현하여 불확실성을 추정치에 통합하는 방법을 알아본다.
또한 Pyro의 유틸리티 기능을 사용하여 TorchScript를 사용하여 예측하고 모델을 서비스하는 방법에 대해 알아본다고 한다.
데이터
Terrain Ruggedness Index(데이터 세트의 험한 변수)로 측정한 국가의 지형 이질성과 1인당 GDP 사이의 관계를 탐구한다.
- rugged: quantifies the Terrain Ruggedness Index
- cont_africa: whether the given nation is in Africa
- rgdppc_2000: Real GDP per capita for the year 2000
import os
from functools import partial
import torch
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import pyro
import pyro.distributions as dist
# for CI testing
smoke_test = ('CI' in os.environ)
assert pyro.__version__.startswith('1.8.1')
pyro.set_rng_seed(1)
# Set matplotlib settings
%matplotlib inline
plt.style.use('default')
DATA_URL = "https://d2hg8soec8ck9v.cloudfront.net/datasets/rugged_data.csv"
data = pd.read_csv(DATA_URL, encoding="ISO-8859-1")
df = data[["cont_africa", "rugged", "rgdppc_2000"]]
df = df[np.isfinite(df.rgdppc_2000)]
df["rgdppc_2000"] = np.log(df["rgdppc_2000"])
회귀 분석(Linear Regression)
우리는 데이터 세트의 두 가지 특징, 즉 국가가 아프리카에 있는지 여부와 지형 견고성 지수의 함수로 한 국가의 1인당 로그 GDP를 예측하고 싶다.
아래 예시에서처럼 PyroModule [nn.Linear]을 하게 되면 우리가 알고 있던 nn.Linear로 사용할 수 있다.
from torch import nn
from pyro.nn import PyroModule
assert issubclass(PyroModule[nn.Linear], nn.Linear)
assert issubclass(PyroModule[nn.Linear], PyroModule)
# Dataset: Add a feature to capture the interaction between "cont_africa" and "rugged"
df["cont_africa_x_rugged"] = df["cont_africa"] * df["rugged"]
data = torch.tensor(df[["cont_africa", "rugged", "cont_africa_x_rugged", "rgdppc_2000"]].values,
dtype=torch.float)
x_data, y_data = data[:, :-1], data[:, -1]
# Regression model
linear_reg_model = PyroModule[nn.Linear](3, 1)
# Define loss and optimize
loss_fn = torch.nn.MSELoss(reduction='sum')
optim = torch.optim.Adam(linear_reg_model.parameters(), lr=0.05)
num_iterations = 1500 if not smoke_test else 2
def train():
# run the model forward on the data
y_pred = linear_reg_model(x_data).squeeze(-1)
# calculate the mse loss
loss = loss_fn(y_pred, y_data)
# initialize gradients to zero
optim.zero_grad()
# backpropagate
loss.backward()
# take a gradient step
optim.step()
return loss
for j in range(num_iterations):
loss = train()
if (j + 1) % 50 == 0:
print("[iteration %04d] loss: %.4f" % (j + 1, loss.item()))
# Inspect learned parameters
print("Learned parameters:")
for name, param in linear_reg_model.named_parameters():
print(name, param.data.numpy())그러면 우리가 저 모델을 사용하면 얻게 되는 결과는 다음과 같다.
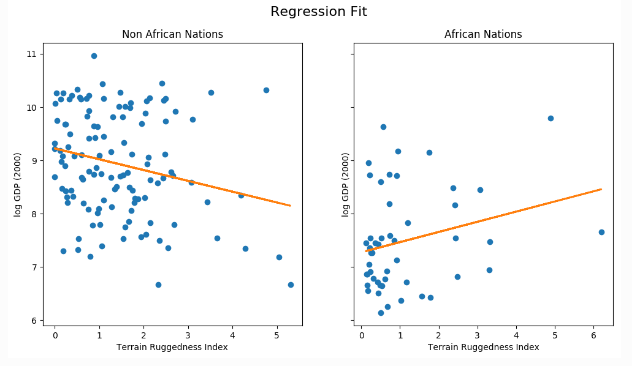
우리는 지형 험준함 사이의 관계가 비아프리카 국가의 경우 GDP와 역관계이지만 아프리카 국가의 경우 GDP에 긍정적인 영향을 미친다는 것을 알아차렸다.
이러한 방식은 점 추정이라고 한다.
하지만 이러한 결과에는 아쉬움이 있다.
이 추세가 얼마나 강력한지는 불분명하다. 특히, 모수 불확실성(parameter uncertainty)으로 인해 회귀 적합성이 어떻게 변화하는지 알고 싶다.
이를 해결하기 위해 선형 회귀를 위한 간단한 베이지안 모델을 구축할 것이다.
베이지안 모델링은 모델 불확실성에 대한 추론을 위한 체계적인 프레임워크를 제공한다.
베이지안 모델링을 사용하면, 단순히 점 추정치를 학습하는 대신, 우리는 관측된 데이터와 일치하는 모수에 대한 분포를 배울 수 있다.
from pyro.nn import PyroSample
class BayesianRegression(PyroModule):
def __init__(self, in_features, out_features):
super().__init__()
self.linear = PyroModule[nn.Linear](in_features, out_features)
self.linear.weight = PyroSample(dist.Normal(0., 1.).expand([out_features, in_features]).to_event(2))
self.linear.bias = PyroSample(dist.Normal(0., 10.).expand([out_features]).to_event(1))
def forward(self, x, y=None):
sigma = pyro.sample("sigma", dist.Uniform(0., 10.))
mean = self.linear(x).squeeze(-1)
with pyro.plate("data", x.shape[0]):
obs = pyro.sample("obs", dist.Normal(mean, sigma), obs=y)
return mean
베이지안 회귀 분석(Bayesian Regression)
선형 회귀를 베이지안으로 만들기 위해서는 매개변수 w와 b에 우선순위를 둘 필요가 있다.
이것은 w와 b에 대한 합리적인 값에 대한 사전 믿음을 나타내는 분포입니다(데이터를 관찰하기 전).
즉 w와 b의 사전 분포를 일단 정의해야 한다.
아래와 같이 nn.Linear로 하게 되고, 각각 weight와 bias에 Pyro Sample을 가정한다.
여기서는 일단 사전적인 것으로 가중치는 평균이 0이고 편차가 1인 정규 분포를 가정하였고,
bias은 평균이 0이고 편차가 10인 정규분포를 가정했다.
아래에서 to_event라고 한 것은 단일 이벤트로 처리하고자 할 때 사용하고 그 말은 즉 변수들 간의 상관관계가 없는 독립적은 것을 가정으로 한다고 볼 수 있다.
MultivariateNormal(zeros(D), eye(D))와 같이 공분산이 없는 것을 가정한다.
왜 저기서 to_event가 2인지는 잘 모르겠다. 인풋은 3개인데...
암튼 그런 식으로 학습하고자 하는 파라미터를 정의한 것이 결국 우리가 타겟으로 하는 분포의 평균을 타겟으로 하는 것이고 forward에서는 그 평균과 편차를 또 가정해서 노말이라고 하고 이 노말 값이 결국에 y라는 관측치를 통한다고 plate로 정의한다.
여기서는 일단 weight로는 3개의 파라미터가 있고, bias가 있고 그리고 sigma가 있어서 총 5개를 학습한다고 볼 수 있다.
weight : 3개
bias : 1개
sigma : 1개
from pyro.nn import PyroSample
class BayesianRegression(PyroModule):
def __init__(self, in_features, out_features):
super().__init__()
self.linear = PyroModule[nn.Linear](in_features, out_features)
self.linear.weight = PyroSample(dist.Normal(0., 1.).expand([out_features, in_features]).to_event(2))
self.linear.bias = PyroSample(dist.Normal(0., 10.).expand([out_features]).to_event(1))
def forward(self, x, y=None):
sigma = pyro.sample("sigma", dist.Uniform(0., 10.))
mean = self.linear(x).squeeze(-1)
with pyro.plate("data", x.shape[0]):
obs = pyro.sample("obs", dist.Normal(mean, sigma), obs=y)
return meanAutoGuide 사용
추론을 하기 위해, 즉 관찰되지 않은 매개 변수에 대한 사후 분포를 학습하기 위해, Pyro는 확률적 변동 추론(SVI)을 사용한다.
가이드는 분포 패밀리를 결정하고 SVI는 실제 사후 분포에서 KL Divergence가 가장 낮은 이 패밀리의 대략적인 사후 분포를 찾는 것을 목표로 한다.
여기서는 guide로 사용할 분포 패밀리를 AutoDiagonalNormal로 정했다.
즉, 잠재 변수 사이에 상관관계가 없다고 가정한다(제2부에서 볼 수 있는 상당히 강력한 모델링 가정).
이런 것처럼 베이지안을 사용하게 되면, 두 분포 간의 상관성 여부도 같이 고려해야 해서 고민할 부분이 많다.
이것은 모델의 각 표본 문장에 해당하는 학습 가능한 매개 변수를 가진 정규 분포를 사용하는 가이드를 정의한다
예를 들어, 이 분포는 각 항에 대한 3개의 회귀 계수에 해당하는 크기 (5,)를 가져야 하며, 절편 항과 시그마 각각에 의해 기여되는 1개의 성분을 가져야 한다.
Autoguide는 AutoDelta로 MAP 추정 학습을 지원하거나 AutoGuideList로 가이드 작성을 지원합니다(자세한 내용은 문서 참조).
from pyro.infer.autoguide import AutoDiagonalNormal
model = BayesianRegression(3, 1)
guide = AutoDiagonalNormal(model)
Optimizing the Evidence Lower Bound
추론을 위해서 Stochastic Variational Inference(SVI)를 사용한다.
비베이지안 회귀 분석 모델처럼 학습 루프의 각 ITERATION에서 GRADIENT STEP을 취하게 된다.
차이점으로는, MSE대신에 Evidence Lower Bound(ELBO)라는 목적을 기준으로 학습하게 한다.
즉, 기존 베이지안처럼 실제값을 직접적으로 학습한다기보다는 추정되는 분포를 따라가게 파라미터가 학습된다는 이야기로 들린다.
from pyro.infer import SVI, Trace_ELBO
adam = pyro.optim.Adam({"lr": 0.03})
svi = SVI(model, guide, adam, loss=Trace_ELBO())여기서는 Adam이라는 Optimizer를 사용한다.
pyro.optimizer의 Optimizer는 Pyro의 파라미터 저장소에서 파라미터 값을 최적화하고 업데이트하는 데 사용된다.
특히, 학습 가능한 매개 변수는 가이드 코드에 의해 결정되고 SVI 클래스 내 장면 뒤에서 자동으로 발생하기 때문에 최적기에 전달할 필요가 없다.
ELBO 그레이디언트 단계를 밟기 위해 우리는 단순히 SVI의 step 방법이라고 부른다. SVI.step에 전달하는 데이터 인수는 model()과 guide()에 모두 전달됩니다. 전체 교육 루프는 다음과 같습니다.
pyro.clear_param_store()
for j in range(num_iterations):
# calculate the loss and take a gradient step
loss = svi.step(x_data, y_data)
if j % 100 == 0:
print("[iteration %04d] loss: %.4f" % (j + 1, loss / len(data)))Pyro param store로부터 최적화된 파라미터를 볼 수 있다.
보시다시피 점 추정치 대신 학습된 모수에 대한 불확실성 추정치(AutoDiagonalNormal.scale)가 있습니다.
autoguide는 잠재 변수를 단일 텐서로 포장하는데, 이 경우 우리 모델에서 샘플링된 변수당 하나의 항목이다.
loc 및 scale 매개 변수 모두 앞에서 설명한 것처럼 모델의 각 잠재 변수에 대해 하나씩 크기(5,)를 가지고 있습니다.
즉, 기존 회귀 분석은 점추정이라고 어떻게 보면 loc에 대한 결과가 나왔다 하면, 여기서는 그 loc에 대한 편차까지 나올 수 있다.
guide.requires_grad_(False)
param_store = []
for name, value in pyro.get_param_store().items():
print(name, pyro.param(name).detach().numpy())
param_store.append(pyro.param(name).detach().numpy().tolist())
AutoDiagonalNormal.loc Parameter containing:
tensor([-2.2371, -1.8097, -0.1691, 0.3790, 9.1824])
AutoDiagonalNormal.scale tensor([0.0552, 0.1143, 0.0387, 0.0769, 0.0700])나온 값을 분포화로 하면 다음과 같이 나온다.
for i in list(zip(*param_store)) :
plt.hist(np.random.normal(loc=i[0],scale=i[1],size=1000))
else :
plt.show()
잠재 모수의 분포를 보다 명확하게 보기 위해, 우리는 AutoDiagonalNormal.quantiles를 사용할 수 있다.
quantile 방법은 AutoGuide에서 잠재된 샘플을 풀고 사이트의 지지대로 자동으로 제한한다.
(예: 변수 시그마는 (0, 10)에 있어야 함).
모수에 대한 중위수 값이 첫 번째 모델에서 얻은 최대우도점 추정치에 상당히 가깝다는 것을 알 수 있다.
즉 값을 좀 잘라서 조건에 만족하는 값을 얻을 수 있게 한다는 느낌인 듯하다
guide.quantiles([0.25, 0.5, 0.75])
{'sigma': tensor([0.9327, 0.9647, 0.9976]),
'linear.weight': tensor([[[-1.8868, -0.1952, 0.3272]],
[[-1.8097, -0.1691, 0.3790]],
[[-1.7325, -0.1430, 0.4309]]]),
'linear.bias': tensor([[9.1351],
[9.1824],
[9.2296]])}
Model Evaluation
모델을 평가하기 위해 몇 가지 예측 샘플을 생성하고 사후 분포를 살펴보겠습니다. 이를 위해 우리는 Predictive 유틸리티 클래스를 사용할 것입니다.
훈련된 모델로부터 800개의 샘플을 생성한다. 내부적으로, 이것은 먼저 가이드에서 관찰되지 않은 사이트에 대한 샘플을 생성한 다음 가이드에서 샘플링된 값으로 사이트를 조건화하여 모델을 실행함으로써 수행된다.
(예측 클래스의 작동 방식에 대한 자세한 내용은 모델 서비스 섹션을 참조하십시오.(
return_sites에서는 결과("obs" 사이트)와 회귀선을 캡처하는 모델의 반환 값("_RETURN")을 모두 지정합니다. 또한 회귀 계수를 캡처하(linear.weight "으로 제공됨).가중치("weight")).
나머지 코드는 단순히 모델의 두 변수에 대한 90% CI를 표시하는 데 사용됩니다.
즉 간단하게 이해한 것으로는 관측치 전체랑 학습된 분포로부터 800개의 가중치를 뽑아내서 다 계산해본다.
그 뽑아낸 값을 기반으로 예측값을 내뱉고, 그 결과에 대해서 평균, 오차, 분 위수를 뽑는다.
그러면 credible interval을 얻을 수 있다는 뜻이다.
from pyro.infer import Predictive
def summary(samples):
site_stats = {}
for k, v in samples.items():
site_stats[k] = {
"mean": torch.mean(v, 0),
"std": torch.std(v, 0),
"5%": v.kthvalue(int(len(v) * 0.05), dim=0)[0],
"95%": v.kthvalue(int(len(v) * 0.95), dim=0)[0],
}
return site_stats
predictive = Predictive(model, guide=guide, num_samples=800,
return_sites=("linear.weight", "obs", "_RETURN"))
samples = predictive(x_data)
pred_summary = summary(samples)
mu = pred_summary["_RETURN"]
y = pred_summary["obs"]
predictions = pd.DataFrame({
"cont_africa": x_data[:, 0],
"rugged": x_data[:, 1],
"mu_mean": mu["mean"],
"mu_perc_5": mu["5%"],
"mu_perc_95": mu["95%"],
"y_mean": y["mean"],
"y_perc_5": y["5%"],
"y_perc_95": y["95%"],
"true_gdp": y_data,
})
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 6), sharey=True)
african_nations = predictions[predictions["cont_africa"] == 1]
non_african_nations = predictions[predictions["cont_africa"] == 0]
african_nations = african_nations.sort_values(by=["rugged"])
non_african_nations = non_african_nations.sort_values(by=["rugged"])
fig.suptitle("Regression line 90% CI", fontsize=16)
ax[0].plot(non_african_nations["rugged"],
non_african_nations["mu_mean"])
ax[0].fill_between(non_african_nations["rugged"],
non_african_nations["mu_perc_5"],
non_african_nations["mu_perc_95"],
alpha=0.5)
ax[0].plot(non_african_nations["rugged"],
non_african_nations["true_gdp"],
"o")
ax[0].set(xlabel="Terrain Ruggedness Index",
ylabel="log GDP (2000)",
title="Non African Nations")
idx = np.argsort(african_nations["rugged"])
ax[1].plot(african_nations["rugged"],
african_nations["mu_mean"])
ax[1].fill_between(african_nations["rugged"],
african_nations["mu_perc_5"],
african_nations["mu_perc_95"],
alpha=0.5)
ax[1].plot(african_nations["rugged"],
african_nations["true_gdp"],
"o")
ax[1].set(xlabel="Terrain Ruggedness Index",
ylabel="log GDP (2000)",
title="African Nations");그래서 아래 그림처럼 샘플이 없는 부분에서는 불확실성이 높게 나오고, 샘플이 있는 부분에서는 CI가 낮게 나오는 결과를 얻을 수 있다.
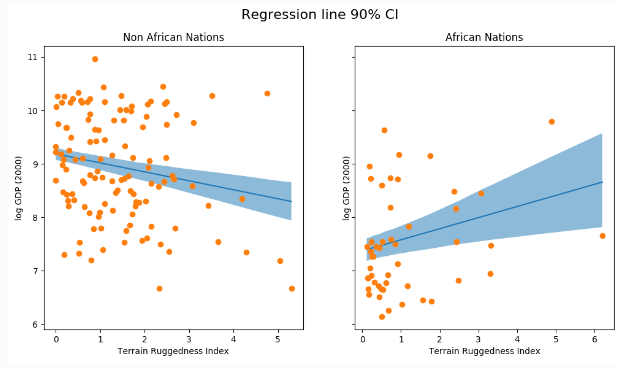
위 그림은 회귀선 추정치의 불확실성과 평균 주변의 90% CI를 보여준다.
또한 대부분의 데이터 포인트가 실제로 90% CI 밖에 있다는 것을 알 수 있으며, 시그마의 영향을 받을 결과 변수를 플롯하지 않았기 때문에 이러한 결과가 예상된다.
모델의 결과와 90% CI가 실제로 관찰하는 대부분의 데이터 포인트를 설명한다는 것을 관찰했다.
일반적으로 모델이 유효한 예측을 제공하는지 확인하기 위해 사후 예측 검사를 수행하는 것이 좋습니다.
위의 그림과 다르게 아래 그림 같은 경우 우리가 결국 관측치(y)에 대한 분포를 가정한 것에 대한 결과이다.
총샘플이 170개가 있는데, 그때 각각의 평균과 편차를 가지는 노말 분포에 대한 결과값을 그린 결과이다.
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 6), sharey=True)
fig.suptitle("Posterior predictive distribution with 90% CI", fontsize=16)
ax[0].plot(non_african_nations["rugged"],
non_african_nations["y_mean"])
ax[0].fill_between(non_african_nations["rugged"],
non_african_nations["y_perc_5"],
non_african_nations["y_perc_95"],
alpha=0.5)
ax[0].plot(non_african_nations["rugged"],
non_african_nations["true_gdp"],
"o")
ax[0].set(xlabel="Terrain Ruggedness Index",
ylabel="log GDP (2000)",
title="Non African Nations")
idx = np.argsort(african_nations["rugged"])
ax[1].plot(african_nations["rugged"],
african_nations["y_mean"])
ax[1].fill_between(african_nations["rugged"],
african_nations["y_perc_5"],
african_nations["y_perc_95"],
alpha=0.5)
ax[1].plot(african_nations["rugged"],
african_nations["true_gdp"],
"o")
ax[1].set(xlabel="Terrain Ruggedness Index",
ylabel="log GDP (2000)",
title="African Nations");마지막으로, 지형 울퉁불퉁함과 GDP 사이의 관계가 우리 모델의 매개 변수 추정치의 불확실성에 대해 얼마나 견고 한 지에 대한 이전의 질문을 다시 살펴보자.
이를 위해 아프리카 안팎의 국가에 대한 지형 울퉁불퉁함을 고려한 로그 GDP의 기울기 분포를 그린다.
아래에서 볼 수 있듯이, 아프리카 국가들의 확률 질량은 대체로 양의 지역에 집중되어 있고 다른 국가들의 확률 질량은 원래의 가설에 더욱 신빙성을 부여한다.
(궁금증 : 왜 2개의 weight를 더함에 따라서 나눠지는지 이해가 잘 안 됨. 두 분포를 더하면 그런 의미가 된다는 것인지?)
이 그림은 왜 저렇게 해석할 수 있는지 이해가 안 됨...
weight = samples["linear.weight"]
weight = weight.reshape(weight.shape[0], 3)
gamma_within_africa = weight[:, 1] + weight[:, 2]
gamma_outside_africa = weight[:, 1]
fig = plt.figure(figsize=(10, 6))
sns.distplot(gamma_within_africa, kde_kws={"label": "African nations"},)
sns.distplot(gamma_outside_africa, kde_kws={"label": "Non-African nations"})
fig.suptitle("Density of Slope : log(GDP) vs. Terrain Ruggedness");
모델 서빙
운영에서도 사용할 수 있다는 예시
trace를 사용해서 다시 구성을 해줘야 한다
from collections import defaultdict
from pyro import poutine
from pyro.poutine.util import prune_subsample_sites
import warnings
class Predict(torch.nn.Module):
def __init__(self, model, guide):
super().__init__()
self.model = model
self.guide = guide
def forward(self, *args, **kwargs):
samples = {}
guide_trace = poutine.trace(self.guide).get_trace(*args, **kwargs)
model_trace = poutine.trace(poutine.replay(self.model, guide_trace)).get_trace(*args, **kwargs)
for site in prune_subsample_sites(model_trace).stochastic_nodes:
samples[site] = model_trace.nodes[site]['value']
return tuple(v for _, v in sorted(samples.items()))
predict_fn = Predict(model, guide)
predict_module = torch.jit.trace_module(predict_fn, {"forward": (x_data,)}, check_trace=False)
torch.jit.save(predict_module, './reg_predict.pt')
pred_loaded = torch.jit.load('./reg_predict.pt')
pred_loaded(x_data)샘플링을 800번 하면 pred_loaded 할 때마다 다른 결과가 나올 것이다.
그때 나온 3개의 계수 값을 적재한 다음에 각 분포에서 샘플링된 데이터들을 분포라고 다시 가정
"cont_africa", "rugged", "cont_africa_x_rugged"에 대한 가중치 분포에서 샘플들이 나오는 것일 텐데...
결국 학습을 하게 되면 가중치들이 나올 것이고, 가중치의 분포에 따라서 결국 log gdp의 영향을 확인할 수 있다.
즉, 여기서 1,2번만 사용해서 본다는 것이 log(GDP)를 예측하는 데 있어서 결국 Non African과 African은 다르다는 것을 확인할 수 있게 된 것으로 마지막에 이해했다.
weight = []
for _ in range(800):
# index = 1 corresponds to "linear.weight"
weight.append(pred_loaded(x_data)[1])
weight = torch.stack(weight).detach()
weight = weight.reshape(weight.shape[0], 3)
gamma_within_africa = weight[:, 1] + weight[:, 2]
gamma_outside_africa = weight[:, 1]
fig = plt.figure(figsize=(10, 6))
sns.distplot(gamma_within_africa, kde_kws={"label": "African nations"},)
sns.distplot(gamma_outside_africa, kde_kws={"label": "Non-African nations"})
fig.suptitle("Loaded TorchScript Module : log(GDP) vs. Terrain Ruggedness");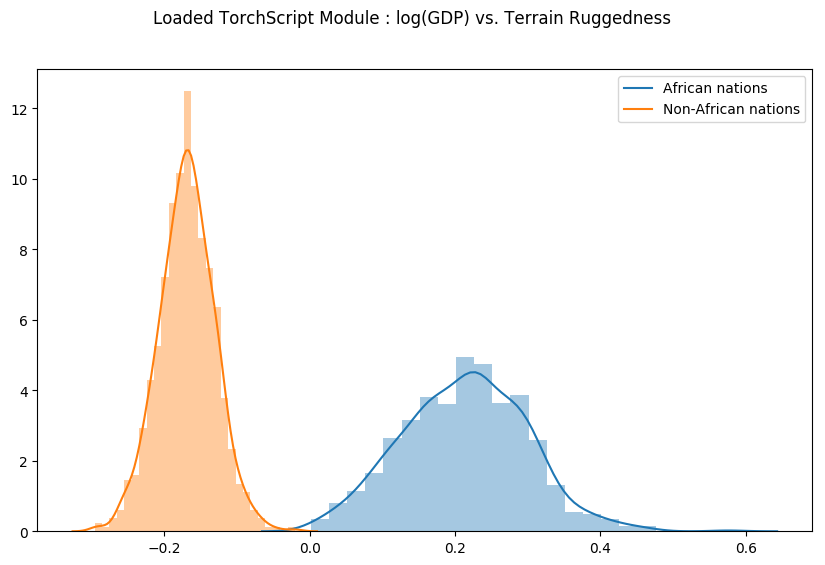
http://pyro.ai/examples/bayesian_regression.html
Bayesian Regression - Introduction (Part 1) — Pyro Tutorials 1.8.1 documentation
Optimizing the Evidence Lower Bound We will use stochastic variational inference (SVI) (for an introduction to SVI, see SVI Part I) for doing inference. Just like in the non-Bayesian linear regression model, each iteration of our training loop will take a
pyro.ai
'분석 Python > Pyro' 카테고리의 다른 글
| [Pyro] Application - 5. GP Bayesian Optimization (0) | 2022.08.29 |
|---|---|
| [Pyro] Application - 4. Gaussian Process Latent Variable Model(GPLVM) (0) | 2022.08.29 |
| [Pyro] Application - 3. Gaussian Process 이해하기 (0) | 2022.08.28 |
| [Pyro] Application - 2. Bayesian Regression 이해하기 2 (0) | 2022.08.28 |
| [Pyro] 개념 파악 및 실습으로 알아보기 (1) | 2022.08.20 |