2022. 8. 29. 00:57ㆍ분석 Python/Pyro
베이지안 최적화는 평가 비용이 많이 드는 objective function를 최소화(또는 최대화) 하기 위한 강력한 전략입니다.
이것은 auto-sklearn,auto-weka 및 scikit-optimize와 같은 자동화된 기계 학습 도구 상자의 중요한 구성 요소이며, 여기서 베이지안 최적화는 모델 하이퍼 매개 변수를 선택하는 데 사용됩니다.
베이지안 최적화는 광범위한 다른 응용 프로그램에도 사용됩니다. 대화형 사용자 인터페이스, 로봇 공학, 환경 모니터링, 정보 추출, 조합 최적화, 센서 네트워크, 적응형 몬테카를로, 실험 설계 및 강화 학습이 포함됩니다.
베이지안 최적화는 특히 파라미터 튜닝할 때 많이 들어보는 내용이고, 목적 함수를 위해서 더 좋은 선택을 할 수 있게 도와주는 알고리즘입니다.
참고 자료
2022.08.21 - [분석 Python/Pyro] - [Pyro] Application - 1. Bayesian Regression 이해하기
2022.08.28 - [분석 Python/Pyro] - [Pyro] Application - 2. Bayesian Regression 이해하기 2
2022.08.28 - [분석 Python/Pyro] - [Pyro] Application - 3. Gaussian Process 이해하기
2022.08.29 - [분석 Python/Pyro] - [Pyro] Application - 5. GP Bayesian Optimization
Problem Setup

최소화 문제를 해결하기 위해, x*에 수렴하는 일련의 점을 구성할 것입니다.
고정된 budget이 있다고 암시적으로 가정하기 때문에 (예를 들어 100개의 평가) 정확한 최솟값을 찾을 것으로 기대하지 않습니다.
목표는 할당된 budget에 줄 수 있는 가장 근사한 솔루션을 얻는 것입니다.
베이지안 최적화 전략은 다음을 따릅니다.
1. objective function f 의 사전 분포를 정하고, 새로운 포인트에 대한 f를 평가할 때 f(x)를 위해서 모델을 업데이트합니다. 이 모델은 surrogate objective function과 f에 대한 믿음을 반영하는 역할을 합니다.
우리는 베이지안이기 때문에 우리의 믿음은 모델 예측의 불확실성에 대해 체계적으로 추론할 수 있도록 사후적으로 인코딩 됩니다.
2. 사후 평가를 사용하여 평가하고 미분하기 쉬운 "acquisition" 함수 α(x)를 유도합니다(α(x) 최적화가 쉽도록).
f(x)와 대조적으로, 우리는 일반적으로 많은 점 x에서 α(x)를 평가할 것입니다. 그렇게 하는 것이 저렴하기 때문입니다.
3. 수렴할 때까지 반복합니다.

좋은 acquisition function은 사후에 인코딩 된 불확실성을 활용하여 exploration(우리가 거의 알지 못하는 쿼리 지점)과 exploitation(우리가 생각할 수 있는 타당한 이유가 있는 영역의 쿼리 지점) 사이의 균형을 장려해야 합니다.
반복 절차가 진행됨에 따라 에 대한 모델이 발전하고 acquisition function도 발전합니다.
모델이 좋고 합리적인 acquisition function을 선택했다면 acquisition function이 쿼리 포인트를 x*로 안내할 것으로 기대합니다.
이 튜토리얼에서 f에 대한 우리의 모델은 Gaussian Process가 될 것입니다.
특히 Pyro에서 Gaussian Process 모듈을 사용하여 간단한 베이지안 최적화 절차를 구현하는 방법을 살펴보겠습니다.
Library Load
import matplotlib.gridspec as gridspec
import matplotlib.pyplot as plt
import torch
import torch.autograd as autograd
import torch.optim as optim
from torch.distributions import constraints, transform_to
import pyro
import pyro.contrib.gp as gp
assert pyro.__version__.startswith('1.8.1')
pyro.set_rng_seed(1)Define an objective function
데모 목적으로 고려할 목적 함수는 Forrester et al. (2008)

이 목적 함수의 최적 값은 0.75725입니다.
def f(x):
return (6 * x - 2)**2 * torch.sin(12 * x - 4)x = torch.linspace(0, 1,100)
plt.figure(figsize=(8, 4))
plt.plot(x.numpy(), f(x).numpy())
plt.show()
Setting a Gaussian Process prior
가우시안 프로세스는 power과 flexibility으로 인해 함수 사전 분포에 대해 널리 사용되는 선택입니다.
가우시안 프로세스의 핵심은 입력 포인트 쌍의 유사성을 제어하는 공분산 함수입니다.
여기서 우리는 목적 함수에 대한 사전 분포로 가우시안 프로세스를 사용할 것입니다.
입력값과 해당 노이즈가 있는 관측값이 주어지면 모델은 다음 형식을 취합니다.

여기서는 (참조 [1]에서 제안한 바와 같이) Matern 커널을 선택합니다.
많은 회귀 작업에서 사용되는 인기 있는 RBF 커널은 샘플이 무한히 미분 가능한 사전 함수를 생성합니다.
이것은 아마도 대부분의 'black-box' 목적 함수에 대한 비현실적인 가정일 것입니다.
# initialize the model with four input points: 0.0, 0.33, 0.66, 1.0
X = torch.tensor([0.0, 0.33, 0.66, 1.0])
y = f(X)
gpmodel = gp.models.GPRegression(X, y, gp.kernels.Matern52(input_dim=1),
noise=torch.tensor(0.1), jitter=1.0e-4)
다음 도우미 함수 update_posterior는 새 값 x에서 f를 평가할 때마다 gpmodel 업데이트를 처리합니다.
아래 모델 같은 경우 새로운 샘플에 대해서 y값을 얻고 그 값을 기존 x에 추가하고 그걸 다시 설정하고 최적화하는 작업을 계속하는 것을 의미합니다.
def update_posterior(x_new):
y = f(x_new) # evaluate f at new point.
X = torch.cat([gpmodel.X, x_new]) # incorporate new evaluation
y = torch.cat([gpmodel.y, y])
gpmodel.set_data(X, y)
# optimize the GP hyperparameters using Adam with lr=0.001
optimizer = torch.optim.Adam(gpmodel.parameters(), lr=0.001)
gp.util.train(gpmodel, optimizer)Define an acquisition function
acquisition function에 대한 합리적인 옵션이 많이 있습니다.
여기서는 '구현 및 해석이 간단한' 기능인 '‘Lower Confidence Bound(신뢰 하한)' acquisition function을 사용합니다.

여기서 μ(x) 및 σ(x)는 점 x에서 사후의 평균 및 제곱근 분산이고 임의의 상수 κ>0은 착취와 탐색 간의 균형을 제어합니다.
이 획득 함수는 다음 중 하나인 x 선택에 대해 최소화됩니다.
i) μ(x)가 작습니다(exploitation).
ii) σ(x)가 큰 경우(exploration).
κ 값이 크면 불확실성이 높은 영역에서 후보 x를 선호하기 때문에 exploration에 더 많은 가중치를 둡니다.
κ의 작은 값은 대리 목적 함수의 평균인 μ(x)를 최소화하는 후보 x를 선호하기 때문에 exploitation을 장려합니다.
여기서는 κ=2를 사용할 것입니다.
def lower_confidence_bound(x, kappa=2):
mu, variance = gpmodel(x, full_cov=False, noiseless=False)
sigma = variance.sqrt()
return mu - kappa * sigma
필요로 하는 마지막 구성 요소는 acquisition function의 최소화 지점을 (근사적으로) 찾는 방법입니다.
gradient 기반 및 non-gradient 기반 기술을 포함하여 여러 가지 방법으로 진행할 수 있습니다.
여기에서는 그래디언트 기반 접근 방식을 따릅니다.
경사 하강법의 가능한 단점 중 하나는 최소화 알고리즘이 로컬 최솟값에서 멈출 수 있다는 것입니다.
이 문제를 해결하기 위해 (매우) 간단한 접근 방식을 채택합니다.
먼저, 5가지 다른 값으로 최소화 알고리즘을 seed 합니다.
i) 하나는 xn−1, 즉 이전 단계에서 사용된 후보 x로 선택됩니다.
ii) 4개는 목적 함수의 영역에서 무작위로 균일하게 선택됩니다.
그런 다음 각 시드 값에 대한 수렴을 근사화하기 위해 최소화 알고리즘을 실행합니다.
마지막으로 최소화 알고리즘에 의해 식별된 5개의 후보 중에서 획득 함수를 최소화하는 후보를 선택합니다.
find_a_candidate 함수를 보면 다음 후보군을 gradient 방식으로 뽑아는 주는 것 같은데... 원리는 잘 모르겠다...
transform_to의 역할이 먼지 모르겠다.
def find_a_candidate(x_init, lower_bound=0, upper_bound=1):
# transform x to an unconstrained domain
constraint = constraints.interval(lower_bound, upper_bound)
unconstrained_x_init = transform_to(constraint).inv(x_init)
unconstrained_x = unconstrained_x_init.clone().detach().requires_grad_(True)
minimizer = optim.LBFGS([unconstrained_x], line_search_fn='strong_wolfe')
def closure():
minimizer.zero_grad()
x = transform_to(constraint)(unconstrained_x)
y = lower_confidence_bound(x)
autograd.backward(unconstrained_x, autograd.grad(y, unconstrained_x))
return y
minimizer.step(closure)
# after finding a candidate in the unconstrained domain,
# convert it back to original domain.
x = transform_to(constraint)(unconstrained_x)
return x.detach()The inner loop of Bayesian Optimization
위에서 정의한 다양한 도우미 함수를 사용하여 이제 next_x 함수에서 베이지안 최적화의 단일 단계의 주요 논리를 캡슐화할 수 있습니다.
여기서는 여러 개의 후보군 중에서 가장 작은 값을 다음 x로 선택한다.
def next_x(lower_bound=0, upper_bound=1, num_candidates=5):
candidates = []
values = []
x_init = gpmodel.X[-1:]
for i in range(num_candidates):
x = find_a_candidate(x_init, lower_bound, upper_bound)
y = lower_confidence_bound(x)
candidates.append(x)
values.append(y)
x_init = x.new_empty(1).uniform_(lower_bound, upper_bound)
argmin = torch.min(torch.cat(values), dim=0)[1].item()
return candidates[argmin]Running the algorithm
베이지안 최적화가 어떻게 작동하는지 설명하기 위해 알고리즘 진행 상황을 시각화하는 데 도움이 되는 편리한 플로팅 기능을 만듭니다.
def plot(gs, xmin, xlabel=None, with_title=True):
xlabel = "xmin" if xlabel is None else "x{}".format(xlabel)
Xnew = torch.linspace(-0.1, 1.1)
ax1 = plt.subplot(gs[0])
ax1.plot(gpmodel.X.numpy(), gpmodel.y.numpy(), "kx") # plot all observed data
with torch.no_grad():
loc, var = gpmodel(Xnew, full_cov=False, noiseless=False)
sd = var.sqrt()
ax1.plot(Xnew.numpy(), loc.numpy(), "r", lw=2) # plot predictive mean
ax1.fill_between(Xnew.numpy(), loc.numpy() - 2*sd.numpy(), loc.numpy() + 2*sd.numpy(),
color="C0", alpha=0.3) # plot uncertainty intervals
ax1.set_xlim(-0.1, 1.1)
ax1.set_title("Find {}".format(xlabel))
if with_title:
ax1.set_ylabel("Gaussian Process Regression")
ax2 = plt.subplot(gs[1])
with torch.no_grad():
# plot the acquisition function
ax2.plot(Xnew.numpy(), lower_confidence_bound(Xnew).numpy())
# plot the new candidate point
ax2.plot(xmin.numpy(), lower_confidence_bound(xmin).numpy(), "^", markersize=10,
label="{} = {:.5f}".format(xlabel, xmin.item()))
ax2.set_xlim(-0.1, 1.1)
if with_title:
ax2.set_ylabel("Acquisition Function")
ax2.legend(loc=1)
대리 모델 gpmodel에는 이미 4가지 기능 평가가 있습니다.
그러나 pyro는 아직 GP 하이퍼 파라미터를 최적화하지 않았습니다.
그래서 그것을 먼저 하고, 그런 다음 루프에서 next_x 및 update_posterior 함수를 반복적으로 호출합니다.
다음 플롯은 알고리즘의 각 단계에서 가우시안 프로세스 사후 및 해당 획득 함수가 어떻게 변경되는지 보여줍니다.
exploration과 exploitation을 위해 쿼리 포인트가 어떻게 선택되는지 확인하십시오.
일단 gpmodel을 학습하고, 학습된 모델을 기반으로 후보군을 찾아서 가장 작은 f를 만드는 x를 찾고 시각화하고, update_posterior에 값을 추가해서 gpmodel을 한번 더 최적화하고 이 과정을 8번 반복한다.
plt.figure(figsize=(12, 30))
outer_gs = gridspec.GridSpec(5, 2)
optimizer = torch.optim.Adam(gpmodel.parameters(), lr=0.001)
gp.util.train(gpmodel, optimizer)
for i in range(8):
xmin = next_x()
gs = gridspec.GridSpecFromSubplotSpec(2, 1, subplot_spec=outer_gs[i])
plot(gs, xmin, xlabel=i+1, with_title=(i % 2 == 0))
update_posterior(xmin)
plt.show()
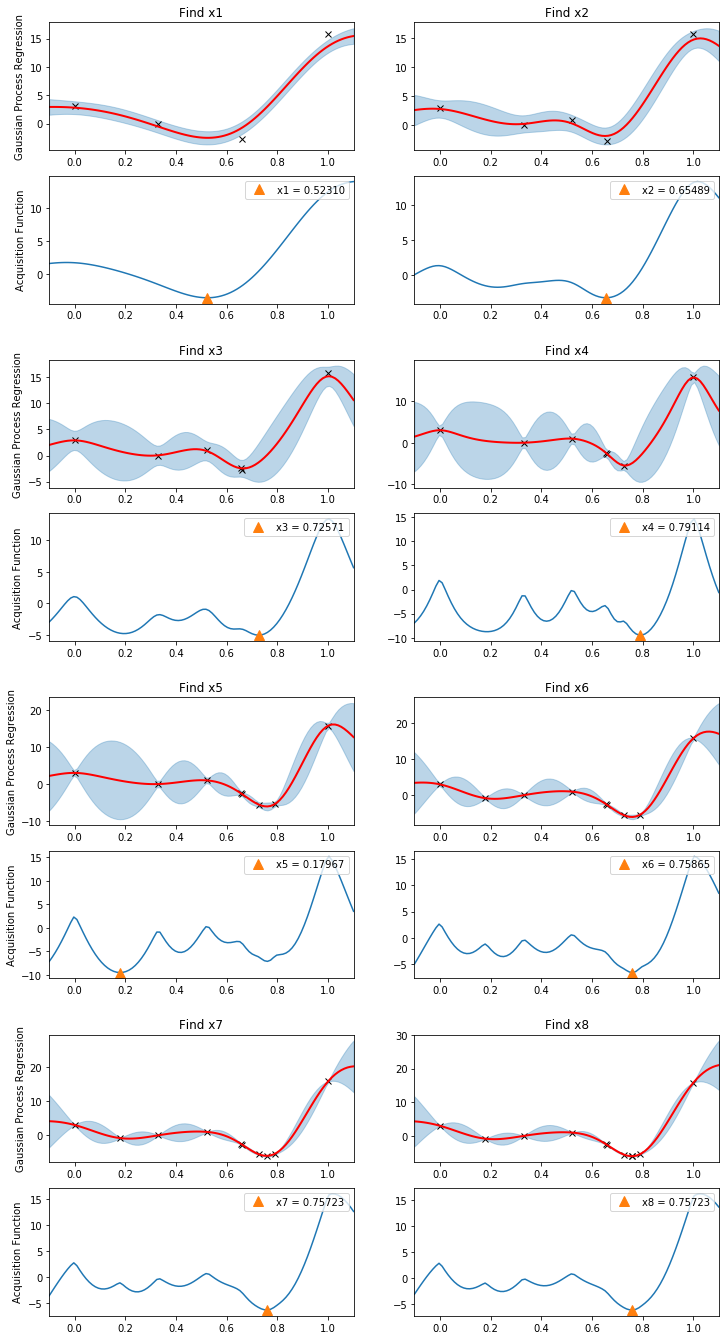
관측값에 노이즈가 포함되어 있다고 가정했기 때문에 함수의 정확한 최솟값을 찾는 것은 불가능합니다.
여전히 상대적으로 적은 평가 budget(8)으로 알고리즘이 x*=0.75725에서 전역 최솟값에 매우 가깝게 수렴되었음을 알 수 있습니다.
이 튜토리얼은 베이지안 최적화에 대한 간략한 소개를 위한 것이지만 기본 기본 아이디어를 전달할 수 있기를 바랍니다.
기본 이론에 대한 훌륭한 설명을 위해 Nando de Freitas [3]의 강의를 시청하는 것을 고려하십시오.
마지막으로 참고 논문[2]은 베이지안 최적화에 대한 최근 연구에 대한 검토와 함께 중요한 기술적 세부 사항에 대한 많은 논의를 제공합니다.
정리
GP를 사용하여 베이지안 최적화를 하는 방법에 대해서 구현된 코드를 봤다.
다른 것은 다 이해가 되지만 다음 후보군을 찾는 것에 대해서는 아직 정확히 이해가 안돼서, 이쪽 부분에 대한 코드를 좀 더 봐야 할 것 같다.
Reference
1] Practical bayesian optimization of machine learning algorithms, Jasper Snoek, Hugo Larochelle, and Ryan P. Adams
[2] Taking the human out of the loop: A review of bayesian optimization, Bobak Shahriari, Kevin Swersky, Ziyu Wang, Ryan P. Adams, and Nando De Freitas
[3] Machine learning - Bayesian optimization and multi-armed bandits
http://pyro.ai/examples/bo.html
'분석 Python > Pyro' 카테고리의 다른 글
| [Pyro] Application - 4. Gaussian Process Latent Variable Model(GPLVM) (0) | 2022.08.29 |
|---|---|
| [Pyro] Application - 3. Gaussian Process 이해하기 (0) | 2022.08.28 |
| [Pyro] Application - 2. Bayesian Regression 이해하기 2 (0) | 2022.08.28 |
| [Pyro] Application - 1. Bayesian Regression 이해하기 (1) | 2022.08.21 |
| [Pyro] 개념 파악 및 실습으로 알아보기 (1) | 2022.08.20 |
데이터분석뉴비님의
글이 좋았다면 응원을 보내주세요!