728x90
N STEP SARSA On-Policy

def gen_epsilon_greedy_policy(n_action, epsilon):
def policy_function(state, Q):
probs = torch.ones(n_action) * epsilon / n_action
best_action = torch.argmax(Q[state]).item()
probs[best_action] += 1.0 - epsilon
action = torch.multinomial(probs, 1).item()
return action
return policy_function
from collections import defaultdictdef n_step_sarsa(env, gamma, n_episode, alpha , n , learn_pi = True):
n_action = env.action_space.n
Q = defaultdict(lambda: torch.zeros(n_action))
policy = {}
for episode in range(n_episode):
state = env.reset()
is_done = False
action = epsilon_greedy_policy(state, Q)
print(Q)
break
s = ['states', 'actions', 'rewards']
n_step_store = defaultdict(list )
for key in s :
n_step_store[key]
n_step_store["states"].append(state)
n_step_store["actions"].append(action)
n_step_store["rewards"].append(0)
t, T = 0 , 10000
while True :
if t < T :
next_state, reward, is_done, info = env.step(action)
next_action = epsilon_greedy_policy(next_state, Q)
n_step_store["states"].append(next_state)
n_step_store["actions"].append(next_action)
n_step_store["rewards"].append(reward)
if is_done :
total_reward_episode[episode] += np.sum(n_step_store["rewards"])
T = t + 1
else :
length_episode[episode] += 1
print(f"{t} / {T}" , end="\r")
tau = t-n + 1
if tau >= 0 :
G = 0
## G만 구하는 과정 (현재 시점)
for i in range(tau + 1, min([tau + n, T]) + 1):
G += (gamma ** (i - tau - 1)) * n_step_store["rewards"][i-1]
## (미래 시점) 더하는 부분
if tau + n < T :
G += (gamma ** n) * Q[n_step_store["states"][tau + n]][n_step_store["actions"][tau + n]]
Q[n_step_store["states"][tau]][n_step_store["actions"][tau]] += alpha * (G - Q[n_step_store["states"][tau]][n_step_store["actions"][tau]])
## On-Policy 바로 바로 학습 n-step 이후로는 바로 학습하는 구조인 듯
if learn_pi :
policy[n_step_store["states"][tau]] = epsilon_greedy_policy(n_step_store["states"][tau], Q)
state = next_state
action = next_action
if tau == (T-1):
break
t += 1
return Q, policy
gamma = 1
n_episode = 500
alpha = 0.4
epsilon = 0.1
epsilon_greedy_policy = gen_epsilon_greedy_policy(env.action_space.n, epsilon)
length_episode = [0] * n_episode
total_reward_episode = [0] * n_episodeimport matplotlib.pyplot as plt
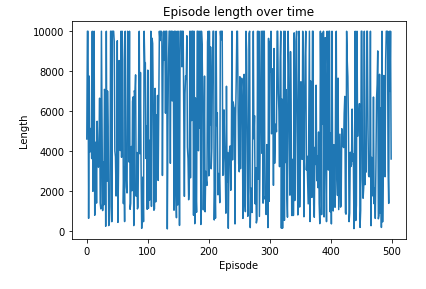
plt.plot(length_episode)
plt.title(f'Episode length over time {min(length_episode)}')
plt.xlabel('Episode')
plt.ylabel('Length')
plt.show()
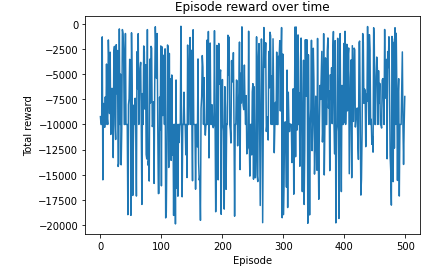
plt.plot(total_reward_episode)
plt.title(f'Episode reward over time {max(total_reward_episode)}')
plt.xlabel('Episode')
plt.ylabel('Total reward')
plt.show()

N STEP Off-Policy SARSA by Importance Sampling

## 아래 코드는 수렴이 안되는 현상이 발생함. 그래서 학습 속도가 굉장히 느림
import torch
from windy_gridworld import WindyGridworldEnv
env = WindyGridworldEnv()
b = {}
for state in range(env.observation_space.n) :
actions = []
probs = []
n_action = env.action_space.n
for action in range(n_action) :
actions.append(action)
probs.append(0.25)
b[state] = (actions , probs)
def gen_epsilon_greedy_policy(n_action, epsilon):
def policy_function(state, Q):
probs = torch.ones(n_action) * epsilon / n_action
best_action = torch.argmax(Q[state]).item()
probs[best_action] += 1.0 - epsilon
action = torch.multinomial(probs, 1).item()
return probs.detach().numpy() , action
return policy_function
from collections import defaultdict
def n_step_sarsa_off_policy_importance_sampling(env, gamma, n_episode, alpha , n , learn_pi = True):
n_action = env.action_space.n
Q = defaultdict(lambda: torch.zeros(n_action))
policy = defaultdict(lambda: np.ones(n_action)/n_action)
for episode in range(n_episode):
state = env.reset()
is_done = False
pi , action = epsilon_greedy_policy(state, Q)
s = ['states', 'actions', 'rewards']
n_step_store = defaultdict(list )
for key in s :
n_step_store[key]
n_step_store["states"].append(state)
n_step_store["actions"].append(action)
n_step_store["rewards"].append(0)
t, T = 0 , 10000
while True :
if t < T :
next_state, reward, is_done, info = env.step(action)
next_pi , next_action = epsilon_greedy_policy(next_state, Q)
if is_done :
total_reward_episode[episode] += np.sum(n_step_store["rewards"])
T = t + 1
else :
length_episode[episode] += 1
next_action = torch.multinomial(torch.tensor(b[next_state][1]), 1).item()
n_step_store["states"].append(next_state)
n_step_store["actions"].append(next_action)
n_step_store["rewards"].append(reward)
print(f"Episode {episode}/{n_episode}, {t:04d} / {T}" , end="\r")
tau = t-n + 1
if tau >= 0 :
rho = 1
for i in range(tau + 1, min([tau + n, T]) + 1):
y = policy[n_step_store["states"][i]][n_step_store["actions"][i]]
x = b[n_step_store["states"][i]][1][n_step_store["actions"][i]]
rho *= y / x
G = 0
for i in range(tau + 1, min([tau + n, T]) + 1):
G += (gamma ** (i - tau - 1)) * n_step_store["rewards"][i-1]
if tau + n < T :
G += (gamma ** n) * Q[n_step_store["states"][tau + n]][n_step_store["actions"][tau + n]]
Q[n_step_store["states"][tau]][n_step_store["actions"][tau]] += alpha * rho * (G - Q[n_step_store["states"][tau]][n_step_store["actions"][tau]])
if learn_pi :
pi, _ = epsilon_greedy_policy(n_step_store["states"][tau], Q)
policy[n_step_store["states"][tau]] = pi
action = next_action
if tau == (T-1):
total_reward_episode[episode] += np.sum(n_step_store["rewards"])
break
t += 1
return Q, policy
gamma = 1
n_episode = 500
alpha = 0.4
epsilon = 0.1
epsilon_greedy_policy = gen_epsilon_greedy_policy(env.action_space.n, epsilon)
length_episode = [0] * n_episode
total_reward_episode = [0] * n_episode
optimal_Q, optimal_policy = n_step_sarsa_off_policy_importance_sampling(env, gamma, n_episode, alpha,3)
print('The optimal policy:\n', optimal_policy)
N STEP Off-Policy Expected SARSA Without Importance Sampling

https://lcalem.github.io/blog/2018/11/19/sutton-chap07-nstep
Sutton & Barto summary chap 07 - N-step bootstrapping
This post is part of the Sutton & Barto summary series.
lcalem.github.io
'관심있는 주제 > RL' 카테고리의 다른 글
| [RL] Create Environment 만들 때 참고 (2) | 2020.09.06 |
|---|---|
| [RL] Continuous Action 일 때 참고 (A2C) (0) | 2020.09.06 |
| 강화학습 기초 자료 모음집 (0) | 2020.07.18 |
| Sarsa, Q-Learning , Expected Sarsa, Double Q-Learning 코드 비교하기 (2) | 2020.07.18 |
| On-Policy와 Off-Policy Learning의 차이 (0) | 2020.07.11 |