강화학습에서 빠르게 코드 비교를 해봤다.
거의 비슷하지만, 다른 부분이 있는 코드들인데, 어떤 식으로 다른지를 보고 싶었다.
막상 비교해보니 큰 차이는 없다는 것을 확인했다.


Model-dependent and model-free reinforcement learning
Model-dependent RL algorithms은 transition table이 있어야 작동을 한다.
transition table은 에이전트가 존재하는 세계에서 성공하기 위해 필요한 모든 지식을 갖춘 테이블이라고 생각하면 된다.
당연히 그러한 테이블을 만드는 것은 매우 지루하며, 불가능하므로 모델 의존 학습 알고리즘은 실용적이지 못하다.
Temporal Difference is a model-free reinforcement learning algorithm.
에이전트는 쉽게 이용할 수 있는 transition table보다는 실제 경험을 통해 학습하는 알고리즘이라는 것을 의미한다. 이를 통해 확률적 요소와 일련의 상태-행동 쌍을 도입할 수 있다. 에이전트는 보상 및 전환 시스템에 대해서는 전혀 모르게 된다. 임의의 상태에서 임의의 행동을 취할 때 어떤 일이 발생할지 알 수 없다. 에이전트는 스스로 환경과 상호작용하여 학습하게 된다.
Temporal Difference Learning
Temporal Difference algorithms 를 통해 에이전트는 모든 단일 작업을 통해 학습할 수 있게 된다.
TD는 모든 에피소드(목표, 종료 시점)이 아닌 모든 시간 단계에서 에이전트의 지식을 업데이트하게 된다.

Target-OldEstimate는 target-error라고 부른다.
위의 식은 매번 업데이트할 때 마다 Target을 달성하는데, 도움이 된다.
Target은 상태의 효용성입니다. 높은 효용성은 에이전트가 더 나은 상태로 되게 한다.
Bellman에 따르면 state의 효용성은 할인된 보상의 기댓값이다.

import torch
from windy_gridworld import WindyGridworldEnv
env = WindyGridworldEnv()
epsilon greed policy 정책 사용

def gen_epsilon_greedy_policy(n_action, epsilon):
def policy_function(state, Q):
probs = torch.ones(n_action) * epsilon / n_action
best_action = torch.argmax(Q[state]).item()
probs[best_action] += 1.0 - epsilon
action = torch.multinomial(probs, 1).item()
return action
return policy_function
from collections import defaultdictSarsa

def sarsa(env, gamma, n_episode, alpha):
"""
Obtain the optimal policy with on-policy SARSA algorithm
@param env: OpenAI Gym environment
@param gamma: discount factor
@param n_episode: number of episodes
@return: the optimal Q-function, and the optimal policy
"""
n_action = env.action_space.n
Q = defaultdict(lambda: torch.zeros(n_action))
for episode in range(n_episode):
state = env.reset()
is_done = False
action = epsilon_greedy_policy(state, Q)
while not is_done:
## S_{t} , A_{t} , R_{t}
### -> S_{t+1}
next_state, reward, is_done, info = env.step(action)
## S_{t+1} -> A_{t+1} (epsilon greedy)
next_action = epsilon_greedy_policy(next_state, Q)
## td error = R_{t} - gamma (Q(S_{t+1}, A_{t+1}) - Q(S_{t}, A_{t}))
td_delta = reward + gamma * Q[next_state][next_action] - Q[state][action]
Q[state][action] += alpha * td_delta
length_episode[episode] += 1
total_reward_episode[episode] += reward
if is_done:
break
state = next_state
action = next_action
policy = {}
for state, actions in Q.items():
policy[state] = torch.argmax(actions).item()
return Q, policy
gamma = 1
n_episode = 500
alpha = 0.4
epsilon = 0.1
epsilon_greedy_policy = gen_epsilon_greedy_policy(env.action_space.n, epsilon)
length_episode = [0] * n_episode
total_reward_episode = [0] * n_episode
optimal_Q, optimal_policy = sarsa(env, gamma, n_episode, alpha)
print('The optimal policy:\n', optimal_policy)import matplotlib.pyplot as plt
plt.plot(length_episode)
plt.title('Episode length over time')
plt.xlabel('Episode')
plt.ylabel('Length')
plt.show()
plt.plot(total_reward_episode)
plt.title('Episode reward over time')
plt.xlabel('Episode')
plt.ylabel('Total reward')
plt.show()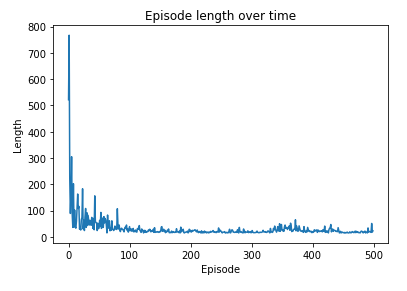

Q-Learning


def q_learning(env, gamma, n_episode, alpha):
"""
Obtain the optimal policy with off-policy Q-learning method
@param env: OpenAI Gym environment
@param gamma: discount factor
@param n_episode: number of episodes
@return: the optimal Q-function, and the optimal policy
"""
n_action = env.action_space.n
Q = defaultdict(lambda: torch.zeros(n_action))
for episode in range(n_episode):
state = env.reset()
is_done = False
while not is_done:
action = epsilon_greedy_policy(state, Q)
next_state, reward, is_done, info = env.step(action)
### 이쪽에서 A_{t+1}도 사용하지 않고 max를 사용한다는 차이가 있음.
td_delta = reward + gamma * torch.max(Q[next_state]) - Q[state][action]
Q[state][action] += alpha * td_delta
length_episode[episode] += 1
total_reward_episode[episode] += reward
if is_done:
break
state = next_state
policy = {}
for state, actions in Q.items():
policy[state] = torch.argmax(actions).item()
return Q, policygamma = 0.99
n_episode = 1000
alpha = 0.4
epsilon = 0.1
epsilon_greedy_policy = gen_epsilon_greedy_policy(env.action_space.n, epsilon)
length_episode = [0] * n_episode
total_reward_episode = [0] * n_episode
optimal_Q, optimal_policy = q_learning(env, gamma, n_episode, alpha)
print('The optimal policy:\n', optimal_policy)
import matplotlib.pyplot as plt
plt.plot(length_episode)
plt.title('Episode length over time')
plt.xlabel('Episode')
plt.ylabel('Length')
plt.show()
plt.plot(total_reward_episode)
plt.title('Episode reward over time')
plt.xlabel('Episode')
plt.ylabel('Total reward')
plt.show()

상태-행동 쌍에 대한 최댓값 대신 각 행동이 현재의 정책 하에 있을 것 같은 정도를 고려한 기댓값을 사용함.
이 알고리즘은 기댓값을 기준으로 이동하는 방향과 같은 방향으로 결정론적으로 이동하게 됨. (무작위 선택 때문에 발생하는 분산을 없애주는 효과가 있다) (일반적으로 살사보다는 좋은 성능을 취하고) (Off-policy alogrithm)이 된다.
Expected SARSA


def sarsa(env, gamma, n_episode, alpha):
"""
Obtain the optimal policy with on-policy SARSA algorithm
@param env: OpenAI Gym environment
@param gamma: discount factor
@param n_episode: number of episodes
@return: the optimal Q-function, and the optimal policy
"""
n_action = env.action_space.n
Q = defaultdict(lambda: torch.zeros(n_action))
for episode in range(n_episode):
state = env.reset()
is_done = False
action = epsilon_greedy_policy(state, Q)
while not is_done:
next_state, reward, is_done, info = env.step(action)
next_action = epsilon_greedy_policy(next_state, Q)
## 여기서 차이가 있음 / max가 아니라 mean 으로 expected 로 계산
td_delta = reward + gamma * Q[next_state].mean() - Q[state][action]
Q[state][action] += alpha * td_delta
length_episode[episode] += 1
total_reward_episode[episode] += reward
if is_done:
break
state = next_state
action = next_action
policy = {}
for state, actions in Q.items():
policy[state] = torch.argmax(actions).item()
return Q, policy
gamma = 1
n_episode = 500
alpha = 0.4
epsilon = 0.1
epsilon_greedy_policy = gen_epsilon_greedy_policy(env.action_space.n, epsilon)
length_episode = [0] * n_episode
total_reward_episode = [0] * n_episode
optimal_Q, optimal_policy = sarsa(env, gamma, n_episode, alpha)
print('The optimal policy:\n', optimal_policy)import matplotlib.pyplot as plt
plt.plot(length_episode)
plt.title('Episode length over time')
plt.xlabel('Episode')
plt.ylabel('Length')
plt.show()
plt.plot(total_reward_episode)
plt.title('Episode reward over time')
plt.xlabel('Episode')
plt.ylabel('Total reward')
plt.show()

현재까지 알고리즘 비교
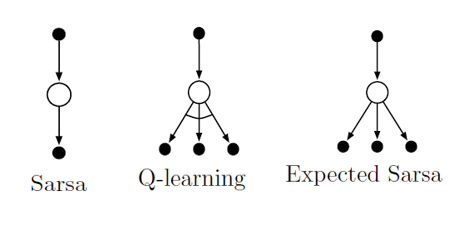
최대화 편차를 해결하기 위한 이중 학습 방법론
최대화 편차란 가치의 추정값 Q(s, a)는 불확실해서 일부는 양수, 일부는 음수인 분포를 가질 때, 최댓값은 0이지만 추정 값의 최댓값은 양수,, 즉 양의 편차 이것을 최대환 편차라고 한다고 함(maximization bias)
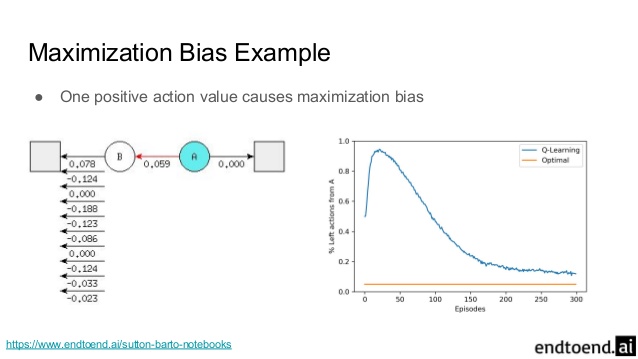
Double Q-Learning


import torch
import gym
env = gym.make('Taxi-v3')
def double_q_learning(env, gamma, n_episode, alpha):
"""
Obtain the optimal policy with off-policy double Q-learning method
@param env: OpenAI Gym environment
@param gamma: discount factor
@param n_episode: number of episodes
@return: the optimal Q-function, and the optimal policy
"""
n_action = env.action_space.n
n_state = env.observation_space.n
Q1 = torch.zeros(n_state, n_action)
Q2 = torch.zeros(n_state, n_action)
for episode in range(n_episode):
state = env.reset()
is_done = False
while not is_done:
action = epsilon_greedy_policy(state, Q1 + Q2)
## S_{t} , A_{t} -> S_{t+1} , R_{t}
next_state, reward, is_done, info = env.step(action)
## 여기가 차이점
## 확률값으로 구분지어 2개를 다르게 구분짓기
if (torch.rand(1).item() < 0.5):
best_next_action = torch.argmax(Q1[next_state])
td_delta = reward + gamma * Q2[next_state][best_next_action] - Q1[state][action]
Q1[state][action] += alpha * td_delta
else:
best_next_action = torch.argmax(Q2[next_state])
td_delta = reward + gamma * Q1[next_state][best_next_action] - Q2[state][action]
Q2[state][action] += alpha * td_delta
length_episode[episode] += 1
total_reward_episode[episode] += reward
if is_done:
break
state = next_state
policy = {}
## Total Q 합치는 부분
Q = Q1 + Q2
for state in range(n_state):
policy[state] = torch.argmax(Q[state]).item()
return Q, policy
gamma = 1
n_episode = 3000
alpha = 0.4
epsilon = 0.1
epsilon_greedy_policy = gen_epsilon_greedy_policy(env.action_space.n, epsilon)
length_episode = [0] * n_episode
total_reward_episode = [0] * n_episode
optimal_Q, optimal_policy = double_q_learning(env, gamma, n_episode, alpha)
import matplotlib.pyplot as plt
plt.plot(length_episode)
plt.title('Episode length over time')
plt.xlabel('Episode')
plt.ylabel('Length')
plt.show()
plt.plot(total_reward_episode)
plt.title('Episode reward over time')
plt.xlabel('Episode')
plt.ylabel('Total reward')
plt.show()

Reinforcement learning: Temporal-Difference, SARSA, Q-Learning & Expected SARSA on python
TD, SARSA, Q-Learning & Expected SARSA along with their python implementation and comparison
towardsdatascience.com
https://medium.com/@qempsil0914/deep-q-learning-part2-double-deep-q-network-double-dqn-b8fc9212bbb2
Deep Q-Learning, Part2: Double Deep Q Network, (Double DQN)
An introduction and implementation tutorial with python3 and Tensorflow
medium.com
'관심있는 주제 > RL' 카테고리의 다른 글
| N-STEP On-Policy SARSA, N-STEP Off-Policy SARSA wiht Importance Sampling, N-STEP Expected SARA 코드 비교해보기 (0) | 2020.07.19 |
|---|---|
| 강화학습 기초 자료 모음집 (0) | 2020.07.18 |
| On-Policy와 Off-Policy Learning의 차이 (0) | 2020.07.11 |
| 강화학습 Action-Selection Strategies for Exploration (0) | 2020.06.27 |
| Chapter 5 Monte-Carlo Learning 공부 (0) | 2020.05.16 |