
광고 한 번만 눌러주세요! 블로그 운영에 큰 힘이 됩니다 ( Click my ADs! )
적용 예제는 해당 블로그에 있으니 참고 바란다.
- Apply Tensor flow 1.x (SHAP or LIME) to tabular data
- [ Python ] SHAP (SHapley Additive exPlanations) Decision plot 설명
- [ Python ] Scikit-Learn Pipeline + RandomizedSearchCV + shap,eli5
SHAP이라는 XAI Library를 사용하려고 하니, 막상 SHAP에 대해 잘 알지 못하는 것 같아서 글을 하나씩 읽어보면서 알아보려고 한다.
머신러닝 분야에서 중요한 질문은 왜 이 알고리즘이 이러한 결정을 했는지이다.
이것은 여러 가지 이유로 중요하다. end user로써, 나에게 노출된 이유를 이해하면 추천 사항을 신뢰할 가능성이 높다.
organization로써, 이 캠페인이 특히 효과적이었기 때문에 고객들이 구매했다는 것을 이해하는 것은 기업에서의 미래 홍보 노력을 조정할 수 있게 해 준다.
그러나 이것은 아직 어려움이 있고, 여전히 머신 러닝에서 연구되는 분야이다.
저 포스터에서는 모형을 해석하는 의미가 무엇인지를 정확하게 논하고, SHAP 기법을 알아본다고 한다.
What does it mean to interpret a model (and why is it so hard)?
모형을 해석하는 의미가 무엇을 정확하게 의미하는지 정의하면서 시작해보자.
매우 높은 레벨에서는 특정 결정일 일으키게 한 것을 이해하는 것을 원할 것이다.
예를 들어, XGBoost 문서로부터 문제를 재사용해보자.
주어진 나이, 성별, 직업에서 computer games을 좋아하는지 안 좋았는지 예측하고 싶다고 하자.

이러한 경우에, 나의 인풋은 나이, 성별, 직업이다. 이러한 feature들이 컴퓨터 게임을 좋아하는지 예측하는 모델에 얼마나 영향을 주는지 알고 싶을 것이다.
이것을 해석하는 방법은 두 가지가 있다.
- On a global level.
전체 데이터셋에서 봤을 때, 어떤 알고리즘이 가장 예측력이 높은 것으로 확인됐는가?
XGBoost의 get_score() 함수(feature를 분할하는 데 사용된 횟수)는 global feature importance를 고려하는 데에 있어서 고려해야 할 하나의 예다. 왜냐하면 그것은 모든 데이터로부터 배운 것을 보기 때문이다. - On a local level
아마도 모든 개인들 중에서 나이가 가장 중요한 특성일 것이고, 젊은 사람들은 컴퓨터 게임을 훨씬 더 좋아하게 될 것이다. 그러나 Frank가 비디오 게임 테스트로 인하는 50세라면, 그의 직업은 그가 컴퓨터를 좋아하는지 여부를 결정하는 데 있어서 나이보다 더 중요하게 작용할 것 같다.
Frank에게 가장 중요한 기능을 식별하는 것은 local에서 feature들을 인지하는 것이 중요하다.
이제는 모델 해석의 큰 어려움 중 하나에 대해서 이야기해보자.
Trading off between interpretability and complexity
간단한 linear regresion을 가정해보자

회귀 분석에서 각각의 변수 x_i에 계수들이 할당되어 있고, 모든 것을 더해서 output을 얻는다.
이러한 경우, 인풋은 age , gender, job이 될 것이다.
이러한 경우에는 feature의 중요성을 찾는 것이 쉽다. 계수의 절댓값이 크다면, 변수 x의 값은 결정을 하는데, 큰 영향을 줄 것이다. (e.g. if ∣ϕ_Age∣ is large, then age was an important feature)
그러나 이것에는 단점이 있다. 왜냐하면 이 모델은 오직 선형 관계에 대해서만 다룰 수 있어서 너무 간단하다.
예를 들어, age가 중요 변수라 할 때 나이가 12-18이면 나이가 더 많은 것보다 중요할 것이다.
왜냐하면 게임을 좋아하는 것과 age의 관계는 비선형적인 관계를 유지하기 때문이다.
선형 관계만 다룰 수 있는 linear model은 비선형 관계를 다룰 수가 없다.
그래서 비선형 관계까지 다루기 위해서는 더 복잡한 모델을 만들 필요가 있다.
그러나 복잡한 모델을 만들게 되면, 이 선형 모형에서 얻은 해석의 용이성을 잃어버렸다. 비선형 관계, 혹은 심지어 서로 얽혀 있는 관계까지도 밝혀내려고 하는 순간. 그 모델을 해석하는 것은 매우 까다로워진다.
(성별에 따라 나이가 중요하다면??)
단순한 관계만 밝혀낼 수 있는 해석하기 쉬운 모델이나 해석하기 어려울지도 모르는 매우 흥미로운 패턴을 발견할 수 있는 복잡한 모델 사이에서의 결정은 해석력과 복잡성 사이에서 trade off 관계이다.
이것은 모형을 해석하고 있을 수도 있다는 사실 때문에 더 복잡하다. 왜냐하면 그 데이터에 대해 뭔가 새롭고 흥미로운 것을 배우기를 희망하기 때문이다. 만약 그렇다면, 선형 모델은 그것을 자를 수 없을 것이다. 왜냐하면 나는 이미 그것이 밝혀낼 관계에 익숙할 수 있기 때문이다.
그러므로 이상적인 경우는 해석할 수 있는 복잡한 모델을 갖는 것이다.
How can we interpret complex models?
선형 회귀에 대해 생각하는 것은 모델 해석에 대한 좋은 사고방식을 낳았다.
x에 계수를 할당할 것이다. 얼마나 output의 영향을 주는지 알 수 있다.
많은 데이터 포인트를 통해, 계수는 복잡한 관계를 찾을 수 없게 될 것이다. 그러나 개별적인 수준에서, 잘할 것이다. 왜냐하면 단일 예측의 경우, 각 변수는 실제로 모델의 예측에 일정한 값에 의해 영향을 미칠 것이기 때문이다.
예를 들어, Frank의 경우 50세의 나이에 게임을 좋아하는 game tester는 job에 대한 계수는 높을 것이고, age 낮을 것이다.
그러나 14살의 바비에게 나이의 계수는 14살의 아이들이 14살이기 때문에 컴퓨터 게임을 좋아하는 경향이 있기 때문에 높을 것이다. 여기서 우리가 한 것은 데이터에서 비선형 패턴을 학습한 복잡한 모델을 개별 데이터 포인트를 설명하는 많은 선형 모델로 세분화한 겁니다.
설명 계수들은 모델의 output이 아니라, 오히려 이 모델을 해석하는 데 사용한다는 것에 주목하는 것은 중요하다.
이러한 모든 단순하고 개별적인 모델을 통합함으로써 우리는 모델이 모든 고객에서 어떻게 행동하는지 이해할 수 있다.
요약컨데, 전체 복잡한 모델을 설명하려고 노력하는 대신에, 잡한 모델을 하나의 데이터 포인트에서 어떻게 행동하는지 설명하는데 노력하기로 했다.
또한 간단한 모형을 더욱 단순화하기 위해 계수 φ을 원래의 특징값으로 곱하지 않고 x. 대신 형상이 있으면 1을 곱하고, 없으면 0을 곱한다.
누가 컴퓨터 게임을 좋아하는지 예측하는 경우에 내가 얻는 것은 다음과 같다.


모든 데이터 포인트에 대해 이 작업을 수행하여 내 모델이 전 세계적으로 어떻게 작동하는지 파악하기 위해 통합할 겁니다. 이제 나는 복잡한 모델을 해석할 수 있는 이 틀을 갖추게 되었으므로, 내가 어떤 속성을 포착하여 유용하게 사용했으면 하는가를 정확히 생각해 볼 필요가 있다.
Shapley values (or, how can I calculate ϕ?)
φ의 가치를 찾는 해법은 머신러닝보다 앞서 있다. 이것은 게임 이론을 기초라 한다.
다음의 시나리오를 고려해보자. 한 무리의 사람들이 게임을 하고 있다. 이 게임을 한 결과, 그들은 일정한 보상을 받는다; 어떻게 그들은 그들의 공헌을 반영하는 방법으로 그들끼리 이 보상을 나눌 수 있을까?
모두가 동의한 몇 가지가 있다. 다음 조건을 충족한다는 것은 게임이 Shapley values에 따라 '공정한' 것이라는 것을 의미한다.
- 모든 사람이 받는 것의 총합은 총보상액과 같아야 한다.
- 만약 두 사람이 같은 값으로 기여한다면, 보상으로부터 같은 양을 받아야 한다.
- 아무것도 기여하지 않은 사람은 아무것도 받을 수 없다.
- 무리가 2개의 게임을 한다면, 그때 두 개의 게임으로부터의 개인의 보상은 첫 번째 게임 보상 + 두 번째 게임 보상과 같아야 한다.
이러한 규칙은 보상을 나눌 때 가져야 할 직관적인 규칙으로 알 수 있으며, 이것은 우리가 해결하려고 하는 머신 러닝 문제에 잘 전달될 수 있다. 머신 러닝 문제에서, 보상은 복잡한 모델의 최종 예측이며 , 게임의 참가자는 특징이다.
이 규칙을 이전 notation안에 적용.
- g_Frank는복잡한 모델이 프랭크에게 컴퓨터 게임을 좋아하게 될 확률)
- 두 특징 x가 최종 예측에 동일한 값을 기여하는 경우, 그 계수 φ는 동일한 값을 가져야 한다.
- 한 특징이 마지막 예측이 기여하는 것이 없다는 기여도는 0이 되여 한다.
- g_(Frank+Bobby) = g_Frank + g_Bobby 여야 한다.
지금까지 우리의 간단한 모델은 기본적으로 규칙 3과 4를 존중한다는 것에 주목할 필요가 있다.
계산하는 방법은 규칙 1과 2도 존중할 수 있도록 한 가지 방법밖에 없는 것으로 밝혀졌다.
Lloyd Shapley은 1953년에 이 방법을 도입했다. (래서 이런 식으로 계산된 φ의 값을 Shapley 값이라고 한다)
주어진 예측 p에서 특정 feature i의 The Shapley values는 다음과 같다.

실제로 보는 것보다 이것은 더 직관적이다. 매우 높은 수준에서, 이 방정식이 하는 것은 featre i가 없는 모형의 예측을 계산하고 형상 i로 모형의 예측을 계산한 다음 차이를 계산하는 것이다.

나는 단지 특징을 추가하고 새로운 형상을 볼 때 모델의 예측이 어떻게 변하는지 알 수 있다.
모델 예측의 변화는 특정 feture의 효과라고 할 수 있다.
그러나 feature을 추가하는 순서는 feature의 값을 할당하는 방법에 중요하다.
왜 이러는지 이해하기 위해 Bobby의 예를 살펴보자. Bobby는 14이고 남자다 이것은 컴퓨터 게임을 좋아할 가능성이 높을 것이다. 이것은 우리가 2번째로 추가하는 기능 중 어느 것이든 불균형적으로 높은 가중치를 갖게 된다는 것을 의미한다.
왜냐하면 모델은 Bobby가 2가지 정보를 모두 가지고 있을 때만, 컴퓨터 게임을 좋아한다는 것을 알게 될 것이기 때문이다.
더 자세한 설명을 위해서, XGBoost 문서에서 의사결정 트리에 피쳐 값을 할당하려고 한다고 가정해 봅시다.
의사결정 트리의 구현에 따라 누락된 값을 처리하는 방법은 다르지만, 이 장난감 예에서는 트리가 분할하는 값이 누락되면 그 아래의 잎의 평균을 계산한다고 하자.

처음에는 Bobby Age 두 번째는 gender이다.
모델이 바비의 나이를 보면, 첫 번째 분할에서 그를 왼쪽으로 데려갈 것이다. 그러면 아직 성별이 없기 때문에 아래의 잎의 평균, 즉 (2 + 0.1) / 2 = 1.05를 그에게 부여할 것이다. 그래서 연령 특성의 효과는 1.05이다.
모델이 그가 남자라는 것을 배울 때, 모델은 2라는 scroe를 얻게 된다. 성별의 효과는 그러므로 2-1.05 = 0.95라고 할 수 있다. 이 시나리오에서는 ϕ_Age Bobby=1.05 and ϕ_Gender Bobby=0.95.
다음은 그의 성별, 그리고 그의 나이를 본다고 하자.
이러한 경우, 성별만 가지고 있을 때 모델은 age로 구별을 할 수 없게 된다. 그러므로 root 아래의 모든 잎의 평균을 가져야 한다. depth 2의 평균은 (2+0.1)/2 = 1.05 이 결과는 depth 1 (1.05 -1)/2 = 0.025
그래서 geneder의 feature의 효과는 0.025가 된다.
그때, 모델은 나이가 14이라는 것일 때, 2점을 얻으니 효과는 (2-0.025) = 1.975가 된다.
So in this scenario, ϕ_Age Bobby=1.975 그리고 ϕ_Gender Bobby=0.025.
φ_agebooby 어떤 값을 할당해야 할까? 만약 우리가 φ_Age Bobby에게 1.975의 값을 할당한다면, 이것은 우리가 φ_Gender Bobby에게 0.025의 값을 할당한다는 것을 의미하는가?
(이 경우 샤플리 공정성의 규칙 1에 따라 총계수는 바비 모델의 최종 예측과 같아야 한다 2)
이는 첫 번째 시퀀스를 무시하기 때문에 이상과는 거리가 멀다. φ_Gender Bobby는 0.95를 받고 φ_Age Bobby는 1.05를 받는다.
Shapley value가 하는 것은 2개의 값을 고려하여 최종 값을 찾기 위해 가중치 합계를 계산하는 것이다.
이것이 φ_i(p)의 방정식이 가능한 모든 feature 그룹 S 집합에서 순열로 배치하는 이유다.
이것은 요약 아래의 S/N/i에 설명되어 있으며, 여기서 N은 모든 특징이다.
합계의 각 구성요소에 가중치를 어떻게 할당하는가?
기본적으로 세트 S에 있는 특징(|S|!)과 아직 추가되지 않은 (n-|S|-1)! 을 모두 고려하여, 세트의 순열이 얼마나 많은지를 고려한다. 마지막으로 가진 특징에 의해 모든 것을 정규화한다.
Calculating a Shapley value
Bobby에게 Shapley는 나이에 비해 어떤 가치가 있을까?
처음에는, sets을 세워야 할 필요가 있다. 나이를 제외하고 bobby 특징들의 모든 가능한 조합들이 있다
왜냐하면, 그는 그의 성별이라는 또 하나의 특징만을 가지고 있기 때문에, 2 셋이 나온다. {x_Gender}, { }
다음으로 각각의 셋 또는 ϕ_i(p)를 계산할 필요가 있다. 여기서 2개니 n=2다.
In the case where S = {}:
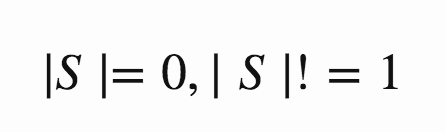
feature가 보이지 않을 때의 모형의 예측은 모든 잎의 평균인데, 우리는 이것을 0.025로 계산했다. 우리는 또한 나이만 보면 1.05라고 계산했다.


In the case where S = {x_Gender}:

나이만 고려하면 0.025이고 나이와 성별을 고려하면 2가 된다.


2개의 값을 총 합하면 다음과 같다.

이 값은 타당하며, 피쳐를 하나씩 추가하는 것만으로 피쳐 중요성을 계산할 때 계산한 값의 중간에 해당된다.
요약해서, Shaple values는 한 개의 특징 없이 모델들의 예측을 비교함으로써, 변수 중요성을 계산할 수 있다.
그러나 모델이 보는 변수들의 순서에 예측이 영향을 받을 수 있기 때문에, 모든 가능한 조합에서 공평하게 변수들을 비교된다.
Shap values
불행히도, 가능한 모든 기능 조합을 통해 빠르게 계산할 수 없게 된다.
다행히 SHAP library는 실질적으로 Shapley value를 사용하게 하는데 최적화되어있다. 그것은 다른 모델의 구조를 이용하는 모델별 알고리즘을 개발함으로써 Shapley 값을 계산한다.
예를 들어, SHAP는 gradient boosted 의사결정 트리와 통합되어 의사결정 트리의 특징에서 계층을 이용하여 SHAP 값을 계산한다.
이를 통해 SHAP 라이브러리는 Feature 조합의 가능한 모든 조합에 대해 모델 예측을 계산해야 하는 경우보다 Shapley value을 훨씬 더 빠르게 계산할 수 있다.
Conclusion
Shapley value와 SHAP 라이브러리는 기계 학습 알고리즘이 식별한 패턴을 발견하는 강력한 도구다.
특히 전처 젝인 데이터셋 대신에 개별 포인트들에서 변수들의 영향을 고려함으로써, 변수들의 조합들의 상호작용을 다룰 수 있다.
이것은 global feature importance 방법보다 훨씬 더 강력한 통찰력을 만들어낼 수 있게 해 준다.
Shapley value에 대해서 잘 몰랐는데, 결국 local interpretability로 고려하는 것이고 뿐만 아니라 변수들의 순서까지도 고려해준다는 것을 알 수 있었다.
https://medium.com/@gabrieltseng/interpreting-complex-models-with-shap-values-1c187db6ec83
Interpreting complex models with SHAP values
Note: This post was originally published on the Canopy Labs website, and describes work I’ve been lucky to do as a data scientist there.
medium.com
'관심있는 주제 > XAI' 카테고리의 다른 글
| Neural Additive Models:Interpretable Machine Learning with Neural Nets (0) | 2020.05.02 |
|---|---|
| Permutation importance 을 사용하여 딥러닝 모델 해석하기 (정형 데이터) (0) | 2020.03.26 |
| 텐서플로우 버전 1에서 LIME 과 SHAP 을 사용하여 모델 해석하기 (정형 데이터) (5) | 2020.02.25 |
| [ Python ] SHAP (SHapley Additive exPlanations) Decision plot 설명 (0) | 2019.09.08 |