
광고 한번만 눌러주세요 ㅎㅎ 블로그 운영에 큰 힘이 됩니다.
모델을 해석하는 방법에는 다양한 방법이 있고, 그중에 많은 패키지는 model-agnostic 한 방법으로 학습된 모델을 사후 해석하는 방향으로 해석을 합니다.
그래서 이번 글에서는 그러한 방법론 중 Permutation을 이용하여 변수 중요도를 구하는 방법을 소개하겠습니다.
여기서 사용하고 있는 많이들 알고 있는 Tensorflow를 사용하여 Neural Network를 기반 아키텍처에 대한 변수에 대한 중요도를 보이고자 합니다.
아래 그림 처름 주어진 데이터에 각 변수마다 Permutation을 통해 다양하게 섞습니다.
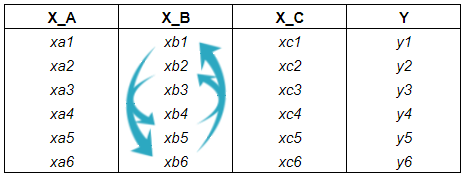
그리고 Permutation을 하였을 때, 결괏값의 Loss가 커질 경우, 그 변수는 중요한 변수라는 것을 의미합니다.
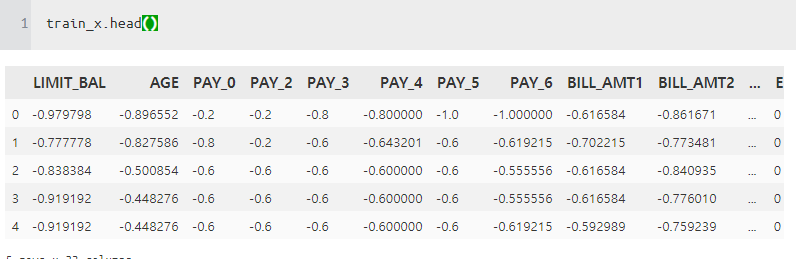
일단 데이터를 전처리를 하고, 학습을 시켜보겠습니다.
모형은 기존에 만들어 놓은 모형이 있어서 그대로 사용하였습니다.
아키텍처는 다음과 같이 간단하게 구성하였습니다.
import tensorflow as tf
tf.reset_default_graph()
X = tf.placeholder(tf.float32 , shape = [None,train_x.shape[1]])
y = tf.placeholder(tf.float32 , shape = [None,1])
batch_size = tf.placeholder(tf.int64)
##
data_tuple = (X,y)
dataset = tf.data.Dataset.from_tensor_slices(data_tuple)
dataset = dataset.shuffle(buffer_size= 1000)
dataset = dataset.batch(batch_size=batch_size, drop_remainder=True)
##
iter = dataset.make_initializable_iterator()
feature_batch , label_batch = iter.get_next()
##
W1 = tf.get_variable("w",shape=[train_x.shape[1],25])
B1 = tf.get_variable("b",shape=[25])
W2 = tf.get_variable("w2",shape=[25,15])
B2 = tf.get_variable("b2",shape=[15])
W3 = tf.get_variable("w3",shape=[15,1])
B3 = tf.get_variable("b3",shape=[1])
##
def Layer(X , reuse = False) :
layer1 = tf.nn.relu(tf.matmul(X, W1) + B1)
layer2 = tf.nn.selu(tf.matmul(layer1, W2) + B2)
logit = tf.matmul(layer2, W3) + B3
return logit
##
logit = Layer(feature_batch)
loss = tf.nn.sigmoid_cross_entropy_with_logits(labels = label_batch , logits=logit)
Loss = tf.reduce_mean(loss)
vars = tf.trainable_variables()
optimizer = tf.train.AdadeltaOptimizer(1e-3).minimize(Loss , var_list = vars)
prob= tf.nn.sigmoid(logit)
auc_value , update_auc = tf.metrics.auc(label_batch , prob , curve="ROC")
output = tf.nn.sigmoid(Layer(X))
tf.add_to_collection('Probability', X)
tf.add_to_collection('Probability', output)>> 중간에 학습이 너무 안되서 고민을 하다가 찾아보니 $AdadeltaOptimizer$가 문제였다.
$$ \text{그래서} AdadeltaOptimizer \text{ -> } AdamOptimizer$$
바로 성능 향상 갓 $Adam$
학습 코드는 다음과 같습니다.
config = tf.ConfigProto(log_device_placement=True)
config.gpu_options.allow_growth = True
EPOCHS = 1000
with tf.Session(config=config) as sess:
saver = tf.train.Saver()
init = tf.group(tf.global_variables_initializer(), tf.local_variables_initializer())
sess.run(init)
for i in range(EPOCHS):
sess.run(iter.initializer ,
feed_dict= {X : train_x.values,
y : train_y.values.reshape(-1,1),
batch_size : 1000}) # switch to train dataset
while True :
try :
probs , _,auc,Loss2,_=sess.run([prob, auc_value,update_auc,Loss,optimizer])
except tf.errors.OutOfRangeError :
break
sess.run(iter.initializer ,
feed_dict= {X : test_x.values,
y : test_y.values.reshape(-1,1),
batch_size : len(test_x)
}) # switch to train dataset
probs , _ , auc = sess.run([prob,auc_value,update_auc])
print(f"Epoch : {i}, AUC : {auc*100:.2f}", end="\r")
meta_graph_bool = True
saver.save(sess,
"./tf_data_test_model.ckpt",
global_step=i, write_meta_graph=meta_graph_bool)
############################################################################
sess.run(iter.initializer ,
feed_dict= {X : train_x.values,
y : train_y.values.reshape(-1,1),
batch_size : len(train_x)
}) # switch to train dataset
original_prob , original_score = np.squeeze(sess.run([prob,Loss]))
final_score = []
shuff_pred = []
for i , indexs in enumerate(pipe[-1].trans_info["onehot_store"]) :
first , to = indexs
diff = to - first
shuff_test = deepcopy(train_x.values)
if diff == 1 :
shuff_test[:,first] =\
np.random.permutation(shuff_test[:,first])
else :
shuff_test[:,first:(first+diff)] =\
np.random.permutation(shuff_test[:,first:(first+diff)])
sess.run(iter.initializer ,
feed_dict= {X : shuff_test,
y : train_y.values.reshape(-1,1),
batch_size : len(shuff_test)}) # switch to train dataset
probs , score = sess.run([prob,Loss])
final_score.append(np.squeeze(score))
shuff_pred.append(np.squeeze(probs))
##########################################################################
중간에 ### 이 부분에서 Permutation을 통해 모델 결괏값을 산출하는 부분입니다.
그다음에 산출된 값을 이용해서 다음과 같이 만듭니다.(임의로 만들다 보니 정말 정확하지 않을 수 있습니다.)
변수 상대적 중요도 = $\frac{|R-P|}{\sum(|R-P|)}*100$
$R$ : 실제 결과 $P$ : Permutation 결과
abs_value = np.abs(final_score-original_score)
FeatureImportance = abs_value / np.sum(abs_value) * 100
plt.subplots(figsize=(15,10))
idx = np.argsort(FeatureImportance)
plt.barh(range(len(totalvar)), FeatureImportance[idx])
plt.yticks(range(len(totalvar)),np.array(totalvar)[idx] ,fontsize= 20)
plt.show()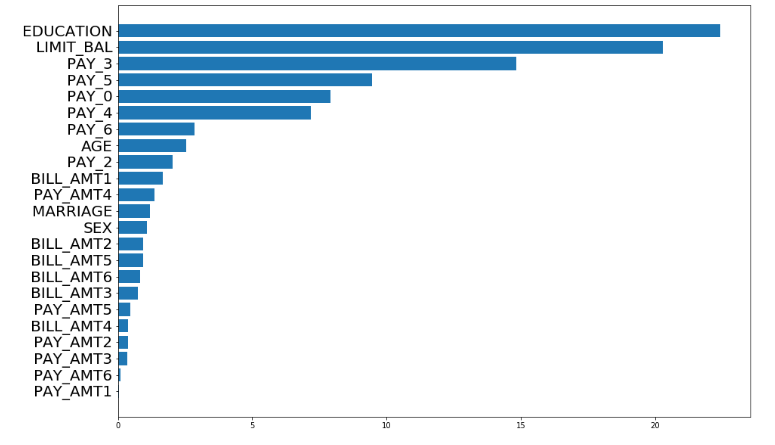
변수 중요도 시각화 코드!
columns = X_train.columns.tolist()
def plot_feature_importances_cancer(model,columns):
plt.subplots(figsize=(15,10))
n_features = len(columns)
idx = np.argsort(model.feature_importances_)
plt.barh(range(n_features), model.feature_importances_[idx], align='center')
plt.yticks(np.arange(n_features), np.array(columns)[idx])
plt.xlabel("특성 중요도")
plt.ylabel("특성")
실제 퍼포먼스가 좋지 않은 상태에서 진행해서 결과에 대한 신용은 할 수 없지만,
EDUCATION이라는 변수가 상대적으로 중요하다고 나옵니다.
CAUSATION RELATIONSHIPS
인과관계를 증명하기 위해 많은 방법론이 있다고 합니다.
유명한 것 중에 하나가 Granger Causality Test라고 합니다. 이 기술에 대해서는 잘 모르지만 시계열에서 자주 사용하는 것 같습니다.
인과관계를 증명하기 위해서, 해야 하는 것은 데이터 셔플이 성능 변화에 의미 있는 증거를 제공한다는 것을 증명하는 것입니다.
np.random.seed(33)
random.seed(33)
id_ = 0
merge_pred = np.hstack([shuff_pred[id_], np.squeeze(original_prob)])
observed_diff = abs(shuff_pred[id_].mean() - merge_pred.mean())
extreme_values = []
sample_d = []
for _ in range(10000):
sample_mean = np.random.choice(merge_pred, size=shuff_pred[id_].shape[0]).mean()
sample_diff = abs(sample_mean - merge_pred.mean())
sample_d.append(sample_diff)
extreme_values.append(sample_diff >= observed_diff)
y, x, _ = plt.hist(sample_d, alpha=0.6)
plt.vlines(observed_diff, 0,max(y), colors='red', linestyles='dashed')
plt.title(f"{totalvar[id_]} p-value : {np.sum(extreme_values)/10000}",fontsize=10)
plt.show()
그래서 파란색 막대는 시뮬레이션된 평균의 차이를 나타내는 분포를 나타내고, 실제 관측된 차이는 빨간색으로 표시했습니다. LIMIT_BAL 같은 경우 셔플 없이 이루어진 예측과 함께 평균의 차이가 없다고 말할 수가 없습니다.
즉 이 변수는 인과관계를 증명할 수 없는 변수가 된다는 의미로 해석할 수 있을 것 같다.
$$H_0 : \text{셔플 없이 계산한 평균 차와 셔플 후 계산한 평균 차의 차이가 없다.}$$
$$H_1 : \text{셔플 없이 계산한 평균차와 셔플 후 계산한 평균차의 차이가 있다.}$$
'관심있는 주제 > XAI' 카테고리의 다른 글
| Neural Additive Models:Interpretable Machine Learning with Neural Nets (0) | 2020.05.02 |
|---|---|
| Interpreting complex models with SHAP values - 리뷰 (0) | 2020.02.29 |
| 텐서플로우 버전 1에서 LIME 과 SHAP 을 사용하여 모델 해석하기 (정형 데이터) (5) | 2020.02.25 |
| [ Python ] SHAP (SHapley Additive exPlanations) Decision plot 설명 (0) | 2019.09.08 |