Neural Network를 학습하기 전에 Normalize를 왜 해줘야 할까?

medium을 보다가 평소에 관심을 가진 주제에 대한 글이 있어서 보기로 하였습니다.

단순 번역일 것 같으니, 원본은 아래에 링크를 남겼습니다!

 

실제로 기존에 뉴럴 넷을 학습시킬 때는 다 데이터를 normalize를 해줍니다.

금액이든 , 나이든 변수 같은 것을 다 0 주변으로 모아준다는 이야기죠 

보통 그렇게 하면 장점이 있다고 합니다.

• 학습이 빨라진다.
• 수렴을 빨리한다.

참고로 요즘은 sigmoid activation을 NN에서는 거의 안 쓴다고 합니다. 

다 알다시피, backpropagation 문제도 있죠? Vanishing gradient 나 exploding gradient

이 글에서는 tanh 와 sigmoid로 비교를 합니다.

결론은 tanh가 좋다는 겁니다.

 

• Sigmoid (=logistic sigmoid)
  • 0~1 (항상 양수)
• Tanh
  • -1 ~ 1

 

위에 그림들은 activation과 한번 미분한 것들을 보여주는 그림입니다.

보면 알 듯이 , sigmoid는 미분한 값이 굉장히 작게 나오는 것을 알 수 있죠?

그래서 학습시 더 빠르게 0으로....

 

이 글에서는 gradient가 어떻게 되는 지를 보겠다고 합니다.

이진 분류로써 여기선 예를 들고 output layer에 나온 것에만 관심을 가집니다.

 

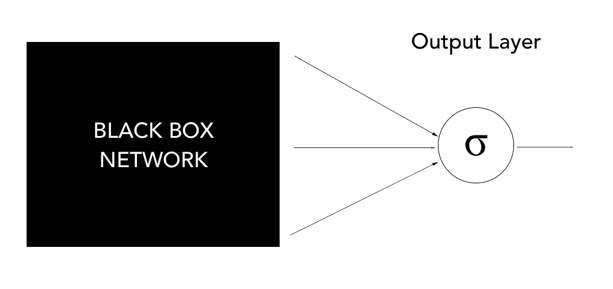
• 마지막 activation을 뭘 주냐에 따라서 output layer는 다양하게 나올 수 있습니다.
• sigmoid를 하게 되면 logistic regression처럼 되는 것 (마지막만 봤을 때)

이진 분류에서 cross entropy의 공식입니다.  y는 타겟 a는 예측된 값입니다.

 

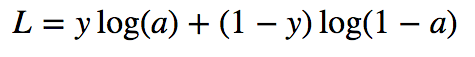
weight 별로 편미분 했을 때 다음과 같은 gradient가 나옵니다.

그러면 보면 알 듯이 x라는 값에 (a-y)가 곱해지는 것을 알 수 있습니다. 

• 그래서 만약 모든 인풋이 같은 방향이면 Gradient도 같은 방향이라는 뜻입니다. [★]
  • 만약 gradient의 방향을 바꾸고 싶으면 `zigzagging`으로써만 할 수 있다고 합니다.
  • zigzagging : 방향의 변화 전에 weight를 빼거나 더하는 행위라고 합니다.
  • 이것은 비효율적!이라고 합니다.

하지만 tanh를 다르다고 합니다.

• 들어오는 x가 -1 , 1로 나올 수 있으므로 방향이 다양하기 때문에 `업데이트되는 방향이 독립적`이가로 합니다. 
• 그래서 쉽게 변화가 가능하고요
• 아래에 이것에 관한 url을 올려줬습니다.

실제 training을 해보면 sigmoid 보다 tanh 모델의 loss가 훨씬 더 같은 에폭에서 잘 떨어진 것을 알 수 있습니다

alpha는 learning rate이고 그 learning rate에 따라서 epoch 10번 후에 어떻게 되는지 보여주는 그래프입니다.

tanh는 비교적 안정적인 모습이지만 sigmoid는 굉장히 불완전해 보이는 것을 알 수 있습니다.

하지만 어떻게 보면 5 에폭까지는 둘 다 잘  되는 것을 알 수 있습니다.

 

다음이 제일 신기했는데요.

Output Layer의 가중치를 시각화한 것입니다.

 

 

 output layer를 보면 모든 것들이 다 같은 방향으로 움직이는 것을 알 수 있습니다.

제가 GAN을 할 때 Output activation을 sigmoid로 했었는데, 이러한 현상이 있었던 거라는 것을 오늘....

Weight가 같은 방향으로 움직이는군요... 여기서 보면 zigzag 움직임을 보이는 것을 알 수 있습니다.

변화의 크기가 다르지만, 변화의 방향이 동일한 것

만약 가중치의 방향성을 바꾸려고 하면, 많은 시간이 소요돼서 지그재그 방향으로 해서 올라가야 할 것입니다.

 

 

오른쪽은 tanh 그림입니다.

tanh는 sigmoid와는 달리 서로 독립적으로 움직이는 것을 알 수 있습니다.

만약 vector의 방향으로 바꾸고 싶을 때 zigzag 할 필요가 없는 것을 알 수 있습니다!

그러니 시간 소요가 덜 되면서 더 나은 수렴을 보여줄 수 있습니다

 

그러면 이게 왜 정규화랑 어떻게 관련되어 있을까?

다시 메인 문제로 돌아가 봅시다. 

장점에 대해서 이야기 해보면은

1. 일단 앞에서 보면 알 듯이 인풋이 같은 방향성으로만 있다면 학습하기가 굉장히 어렵기 때문에정규화를 통해서 + , - 값을 다 가지면 학습을 원활하게 할 수 있습니다.
2. 인풋의 스케일과 연관되어 있습니다. 예를 들어 돈의 단위와 키의 단위는 다릅니다 그래서 이런 것들이 Weight에도 충분히 영향을 줄 수 있기 때문에 이런 것들을 0 주변으로 모아줘서 학습을 시킬 때 도움을 줄 수 있습니다.

 아래 그림을 보면 알 듯이 인풋 x와 관계되어 있습니다. 만약 여기서 인분 값이 크거나 엄청 작다면 Update의 영향을 직접적으로 줄 것입니다. 

그래서 만약 크기가 다른 인풋을 넣게 되면 다른 인풋들보다 업데이트를 더 빠르게 해서 학습적인 측면에서 문제가 될 수 있습니다.

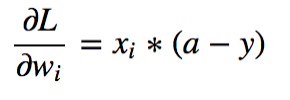
이렇게 됐을 때 만약 진정 중요한 변수가 범위가 작은 것일 때면 영향도를 측정할 수 없을 것입니다.

그래서 Scailing을 통해서 더 중요한 변수도 잘 잡을 수 있게 합니다.

그런데 여기서 드는 생각은 categorical 변수 같은 것이 0 ~ 1 밖에 없어서 너무 극단적인 값만 나와서 좀 

생각이 드네요.

그래서 이전에 포스트 한 Categorical을 Embedding에 대해서 아이디어를 좋다고 생각한 것 같습니다.

https://data-newbie.tistory.com/90

NN에서 Categorical Variables에 대해서는 어떻게 해야할까?

 

결론

• normalization은 양수 음수가 나와서 학습에 방향성에 대해서 독립적으로 만들 수 있습니다 여기서 말한 학습의 방향성이란 Weight를 이야기 하는 것입니다. 그렇게 해서 더 유연하게 학습을 가능하게해서 안할 때 보다 좀 더 학습을 잘하게 된다는 것이지요.
• Scaling을 해줘야 하는 이유는 sigmoid 같은 경우를 보면 큰 값의 단위들은 다 1을 내뱉게 될 것입니다. 그러면 학습은 exploding gradient 그런 것 때문에 숨막히게 학습이 안되겠쬬?

실현과 실천의 차이를 항상 생각하자. 실천은
내 생각대로처럼 되진 않지만, 노력한 것이고
실현은 내 생각을 그대로 구현한 것이다.
죽어라 읽고 고민하고 관찰하고 써보고 해서 머리를 가득 채우자

https://www.youtube.com/watch?v=dqNs1xLAitE

 

원글 참고

https://github.com/timo-stoettner/nn-normalization/blob/master/Tanh%20vs%20Sigmoid%20-%20Notebook.ipynb

https://towardsdatascience.com/why-data-should-be-normalized-before-training-a-neural-network- c626b7f66c7d

Why Data should be Normalized before Training a Neural Network