2021. 5. 29. 17:54ㆍML(머신러닝)/BASIC
개인 공부를 하려는 글로써, 분명히 틀린 부분이 있을 수 있습니다.
혹시 보시는 분이 있다면, 가볍게 봐주시고, 느낌만 알고 싶어서 하는 것이니
틀린 부분이 어디가 틀렸는지 댓글로 알려주시면 정말 감사하겠습니다. :)
이 부분에 대해서 글을 남기고 싶었던 이유는 항상 여기에 대해서 궁금하였는데, 잘 모르게 됐다가, 어느 글을 보고 대충 감이라도 얻게 되어서 정리를 하고 싶어서 남기게 되었다.
Measure Space

algebra
일종의 규칙을 담아 놓은 집합
예시) 위상수학에서의 Topology는 모든 열린 집합들의 집합
A (σ-algebra) or σ-field
모든 가측집합들의 집합

1. 어떤 것이 집합에 있다면, 그것의 여집합도 집합에 있어야 한다.
2. 공집합과 전체집합이 있어야 함
3. 마지막으로 측정 가능한 집합들의 합집합 또한 측정 가능할 것입니다

전체집합, 공집합이 있음 - 2번 조건 만족
A의 여집합 $A^c$ 존재 / 공집합의 여집합 X 존재 - 1번 조건 만족
$AUA^c$은 X로 만족 - 3번 조건 만족
Measurable Space

공간이라 하면 가장 작은 측정 가능한 공간은?
-> 공집합과 전체집합이 있는 것이 가장 작음 F = {0, X}
측정 가능한 공간이라 하면 가장 작은 큰 공간은?
-> 시그마 대수는 어떤 집합의 부분집합의 모임이기 때문에 모든 부분집합의 집합(멱집합; Power set)이 가장 큰 시그마 대수가 될 것입니다. 이는 F=P(S) F=P(S)로 표기합니다.
열린 집합(open set)
열린 집합이라 하면 실수 위의 열린구간 정도를 생각할 수 있겠지만 이건 좁은 의미의 열린 집합이다. 정확한 열린집합의 정의에 의하면 열린구간도 열린집합이 아닐 수 있고 닫힌구간도 열린 집합일 수 있다. 심지어 열린닫힌집합(clopen set) 일 수도 있다!
https://haawron.tistory.com/18
길이(distance) → 거리(metric) → 거리 공간(metric space) → 위상 공간(topological space)
1. 태초에는 두 점 사이의 "길이(distance)"부터 시작했다. 하지만 두 점뿐만 아니라, 분포, 집합 등등의 길이도 정의할 필요성이 생겼다.
2. "길이"의 상위 개념으로 길이의 원초적인 성질을 모아 "거리(metric)"이라는 것을 정의한다.
3. 이제 어떤 집합의 원소들을 다양한 "거리"를 이용해 멀고 가까움을 측정할 수 있게 되었다. 특정 거리(metric)로 측정 가능한 공간을 "거리 공간(metric space)"로 정의한다.
4. 거리 공간에서 이제 우리가 아는 열린 집합을 정의할 수 있게 되었다. (단순히 경계를 포함하지 않는 집합)
5. 하지만 어떤 공간에서도 성립하는 불변량을 사용하려면 "거리가 없는 공간"에서도 성질을 유지해야 할 것이다.
6. 그래서 만들어진 공간이 "위상 공간(topological space)"이며 거리 공간의 열린 집합들의 성질을 모아 위상 공간에서의 열린 집합들을 정의하게 된다.
Borel Set

열린 집합과 σ-field의 개념을 섞으면 된다. 위상 공간(열린 집합들을 모두 포함)에서 measure를 정의(σ-field의 목적)할 수 있게 해 준다.
위상 공간 $(X, T)(X, T)$ 위의 열린 집합(닫힌집합이라고 해도 된다.)들을 포함하는 가장 작은 σ-field를 Borel-algebra라고 하며, 이 집합의 원소를 Borel set이라 한다.
"가장 작은"이라면 "크기(cardinality)가 가장 작은"을 의미할 것이다.

즉 열린 구간 안에서 측정 가능한 집합에 있는 집합의 모든 원소를 Borel-Set이라고 하는 것 같다...
Measurable Function or Measure
집합(σ-algebra)에 있는 값을 실수로 보내버리는 함수

Probability (Measure) space

그렇다면 확률 공간은 어떻게 정의할 수 있을까?
Measure Space에서 어떻게 정의하냐에 따라서 확률 공간이 될 수 있다.
(X, A, u)를 ($\omega,\sigma, P$)로 바꿔주면 이것을 확률 공간이라고 할 수 있다.
그냥 X를 $\omega$ 로만 바꿔서 쓰는 정도로 알면 될 것 같고, 표본 공간(sample space)라고도 부른다.
그리고 확률 공간을 정의하기 위해서는 이벤트라는 것이 필요합니다. 그리고 그 이벤트는 mesurable function에서 다음과 같이 가정을 합니다.
즉 측정 가능한 공간이라는 가정을 합니다.


Sample space $\omega$난 확률적인 실험들의 모든 결과물들을 의미합니다.
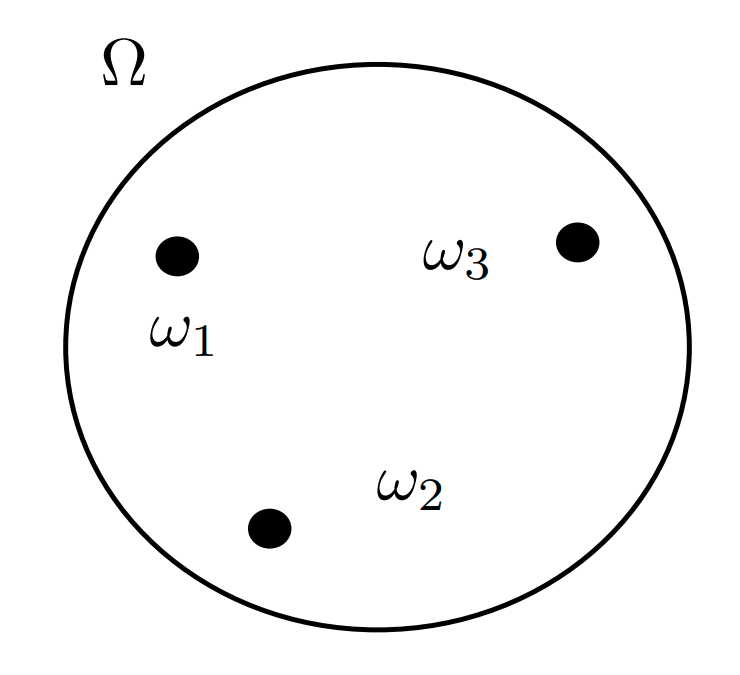
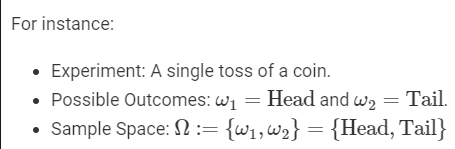
Event Space라는 것은 sigma-algebra on the sample space에 있습니다.
Event Space는 Sample space($\omega$)의 power set의 subset입니다.
여기서는 몇가지 정규성 조건을 다 만족할 때의 subset을 의미합니다.
만약 Sample space($\omega$)가 유한하다면, power set $P(\omega)$는 event space에서 사용된 $\sigma algebra$ 여야 합니다.


그리고 이러한 가축 공간을 실수 집합을 맵핑하는 것을 여기서는 P라고 하고 정의는 다음과 같습니다.

당연히 이 확률이라는 것은 Measurable function을 만족해야 할 것 같습니다.
그래서 확률 공간은 이렇게 정의한다는 것을 배웠습니다.
이 Measurable Function이라는 것은 우리가 흔하게 듣는 random variable이다.

여기서 다시 Probability Distribution 까지 나아가면 다음과 같다.
A probability distribution = pushforward measrue
A probability distribution is also called a pushforward measure of the probability measure P via the random variable X
우리가 확률 공간((Ω,F,P))을 가정한다는 것은 이벤트(F)에다가 확률값들을 할당할 수 있게 된다.
이때 measurable space (E,$\epsilon$)이 있고, 이벤트들을 측정하기 위한 probability measure가 없을 때 우리는 어떻게 $\epsilon$에서 measuring set을 찾을 수 있을까?
핵심 아이디어는 $\epsilon$ 안에 있는 B(Borel Set)이 주어질 때, random variable X를 사용하여 event space에서 해당 집합의 사전 이미지를 찾은 다음 probability measure을 통해 이 집합을 측정할 수 있다는 것이다.

probability distribution 또는 pushforward는 X∗P or P∘X−1. 로 명시되어 있다. 확률 분포는 그러므로 $\epsilon$ 안에서 [0,1]로 맵핑하는 함수이다.

Probability Density Function
measurable space에서 Lebesgue measure $\lambda^n$을 가진다고 하였을 때, 이것을 각 셋(A $\in B(R^n)$에 할당할 수 있다.
그러나 이제 랜덤 변수가 생겼고, 발생 가능성(likelehood)에 따라 집합의 크기($A \in B(R^n)$)를 "weight"하려고 합니다.
이를 위해, 우리는 의 모든 지점에 밀도를 할당하고 그에 따라 의 새로운 측정값을 계산하기 위해 Lebegue 측정값에 따라 모든 지점에서 밀도의 평균을 구해야 한다.

본질적으로 density는 그것이 밀도의 변화 속도를 설명한다는 점에서 derivatrive와 거의 유사하다.
X에 관해서 이러한 이유로, 우리는 밀도를 다음과 같이 나타낸다.
$f = \frac{d X_*\mathbb{P}}{d \lambda^n}.$
이것을 Radon-Nikodym derivate라고 부른다(?)
이 표기법을 사용하면 integration에 사용하는 방법을 변경할 수 있기 때문에 매우 편리합니다.
$X_*\mathbb{P}(A) = \int_A d X_*\mathbb{P} = \int_A \frac{dX_*\mathbb{P}}{d \lambda^n} d\lambda^n = \int_Af d\lambda^n$
이 함수를 random variable X의 probability density function이라고 부른다.
probability distribution도 원래 probability measure로 표현할 수 있는 방법에 주목하면 좋을 것 같다고 합니다.
$p(A) = X_*\mathbb{P}(A) = \int_A d\mathbb{P}\circ X^{-1} = \int_{X^{-1}(A)}d \mathbb{P}$
저번에 몇 번 찾아보고 알아봤지만, 이제야 아주 아주 얇게 기본을 배운 것 같습니다...
https://haawron.tistory.com/18
Mathematics | 왜 하필 Borel Set일까?
Reference https://jjycjnmath.tistory.com/150 https://www.slideshare.net/ssuser7e10e4/wasserstein-gan-i http://iseulbee.tistory.com/attachment/cfile21.uf@213DA24658C01012058757.pdf https://en.wikiped..
haawron.tistory.com
https://maurocamaraescudero.netlify.app/post/visualizing-measure-theory-for-markov-chains/
Visualizing Measure Theory for Markov Chains | Mauro Camara Escudero
Measure-theoretic concepts underpinning the development of Markov Chains and Markov Chains Monte Carlo (MCMC) via insightful diagrams.
maurocamaraescudero.netlify.app
https://bookdown.org/edeftg/machine_learning_with_rust/measuretheory.html
Chapter 3 Measure Theory | Machine Learning with Rust
This is a minimal example of using the bookdown package to write a book. The output format for this example is bookdown::gitbook.
bookdown.org
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=at3650&logNo=220887951885
Introudction to Measure theory : Measureable space and application
지난 첫번째 포스팅에서도 언급을 하였듯이, 우리의 목적은 (1편에 블라블라 떠들어댔던 바와 같이) 새로운...
blog.naver.com
Chapter 1- Elementary mathematics 자료
https://www.edwith.org/bayesiandeeplearning/joinLectures/14426?isDesc=false
Bayesian Deep Learning 강좌소개 : edwith
- 최성준
www.edwith.org
'ML(머신러닝) > BASIC' 카테고리의 다른 글
| 지도 학습에서 사용하는 목적 함수 정리하기 (1) | 2020.03.12 |
|---|---|
| MISSFOREST 알고리즘 설명 (0) | 2019.10.01 |
| 차원 축소에 대한 10가지 팁(Ten quick tips for effective dimensionality reduction) (0) | 2019.08.11 |
| Binary Classification 중 주의해야 할 것과 팁 (0) | 2019.05.30 |
| 모델평가와 성능평가 _미완성 (0) | 2018.01.15 |