흔하게 우리는 여러 가지 분류 문제에 대해서 경험을 하게 된다. 멀티 클래스를 분류해야 하는 경우도 있지만,
흔하게는 이진 분류를 많이 한다.
암이 있는지?없는지? 사기꾼인지? 아닌지? 와 같이 것이 하나의 예다.
분류 문제를 생각하게 된다면, 가장 많이 보는 것이 Confusion matrix 이다.


특정 Cut off를 이용해 2가지 중 하나로 분류해주고, 다음에 쉽게 눈으로 결과의 성능을 보는 역할을 한다.
보통 평가 메트릭으로는 accuracy를 본다.
말 그래도 정확도이기 때문에 많이들 보지만, 여기에는 문제가 있다.
바로 Imbalanced dataset 같은 경우에 문제가 된다.
예를 들어 사기범을 찾고 싶은 모델을 만들고 싶을 때, 사기범은 데이터 중에 얼마나 있을까?
아마 일반인에 비해서 10000 : 1 될 정도로 엄청나게 작은 비율일 것이다.
하지만 Accuracy로 평가를 하게 돼서, 눈감고 다 일반인이라고 예측한다고 할 때 결과는
99.99%가 된다.
우리가 원하는 사기범을 탐지하는 모델인데, 그러한 기능을 전혀 하지 못한다!
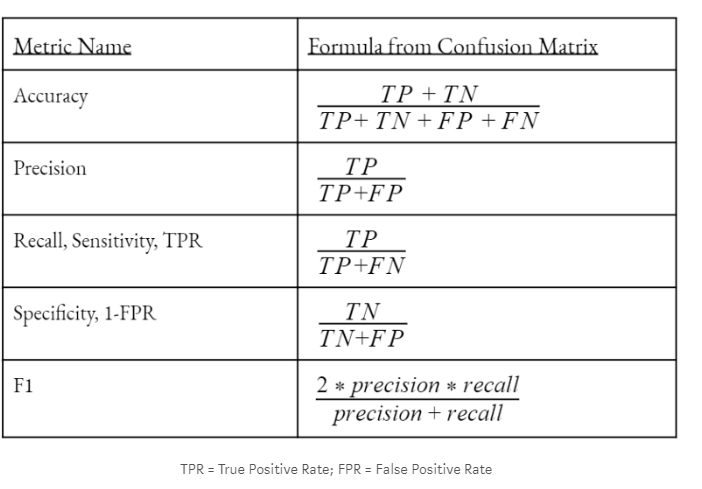
Accuracy = (TP + TN) / (TP + TN + FP + FN) 다음과 공식인데,
결국 평범한 사람을 잘 맞추기만 하면, 성능이 보장되어버리는 metric이라서, 이러한 경우에는 좋지 않은 평가지표다.

그렇다면 우리는 어떠한 measure를 사용해야 할까?
- Sensitivity (or Recall, or True Positive Rate)
Sensitivity = TP / (TP + FN) (실제 발생한 것 중에서 실제로 맞힌 경우)
만약 10명의 탐지 범 중 1명만 모델이 맞추면 성능인 10%로 아주 적게 나온다!
- Specificity (실제 발생하지 않은 사람 중에서 모델이 그러한 경우를 맞힌 경우)
- Specificity = TN / (TN + FP)
- False-positive rate= 1 — Specificity
- Precision (실제 발생을 예측한 것 중에서 진짜 발생을 맞힌 경우)
- Precision = TP / (TP + FP)
여기서 아마 Sensitivity와 Precision에 대해서 헷갈릴 수가 있다.
서로 기준이 다르니, 유념하자. Sensitivity는 진짜 발생을 기준으로 하고,
Precision는 모델이 발생을 예측한 것을 기준으로 하게 된다.
결국 사용자가 어디를 중시하는지에 따라서 서로 다른 접근을 할 수 있을 것 같다.
예를 들어 다음날 비가 오는 경우를 맞추고 싶다.
근데 실제 모델이 비가 온 것 중에서 비가 온 날을 맞춘 것은 50%지만,
모델이 비가 왔다고 예측했을 때 실제 비가 온 것은 80% 일 수 있다.
그러면 모델 성능 자체면에서 볼 때는 좋아 보여서 사용할 수 있고,
그런 것 보다 실제 발생에 대한 경우가 중요하다면, 쓰지 않을 수 있다.
결국 어떠한 관점에서 문제를 보고 싶은지에 따라서 다르게 해석하고 사용할 수 있다!
이런 metric은 결국 평범한 사람을 얼마나 잘 맞췄는지에 대한 metric이라서 우리가 탐지하고 싶은 경우에 대해서는 잘 탐지를 못하지만 결과는 90% 나올 것이다!
Should we maximize specificity or sensitivity?
그렇다면 senstivity와 specificity를 어떻게 하면 최소화해서 대각선에 값들이 모이게 할 수 있을까?
흔히 통계를 배우다 보면 type-1 error(1종 오류)와 type-2 error(2종 오류)를 공부하게 된다.
- 1종 오류
- 귀무가설이 실제로 참이지만, 이에 불구하고 귀무가설을 기각하는 오류
- 즉) 실제 음성인 것을 양성으로 판정하는 경우 (alpha error)
- 2종 오류
- 귀무가설이 실제로 거짓이지만, 귀무가설을 기각하지 못하는 오류
- 즉) 실제 양성인 것을 음성으로 판정하는 오류
둘 다 중요한 오류지만, 만약 직관적으로 봤을 때 2종 오류가 더 중요하다고 생각할 수 있다.
흔히 예를 드는 것이 판사가 재판을 할 때인데,
귀무가설 : 범죄자는 범죄를 저지르지 않았다. 대립 가설 : 범죄자가 범죄를 저질렀다는 것을 기각시킬만한 근거가 없다.
그렇다면 일단 범죄자가 실제로 어떤진 모르겠지만,
만약 범죄를 저지르지 않았는데, 범인이라 하는 경우 (1종 오류)
범죄를 저질렀지만, 범인이라고 하지 않는 경우 (2종 오류)
이러한 경우, 3자 입장에서 봤을 때 당연히 범죄자가 아닌데 범죄자라 하는 경우일 것이다.
그래서 1종 오류에 대해서 중요하게 생각해서 주로 alpha 유의 수준으로 측정한다.
F1 Score
- F1 = 2 * (Precision * Sensitivity) / (Precision + Sensitivity)
F1은 precision과 recall을 조화 평균으로 한 measure다.
이것을 사용하면 2가지에 대해서 다 반영을 하기 때문에 보통 imbalance 할 때 주로 사용한다.
What happens when we change the probability cutoff?
하지만 중요하게 생각할 것이 Precision , Sensitivity는 결국 확률 값이 나왔을 때 특정 cut off를 이용해서 특정 클래스로 분류하고 나서의 결괏값이다. 즉 Cutoff를 어떻게 하는지에 따라서 결과가 많이 달라질 것이다
이러한 cutoff에 대해서 전체적으로 시각 한 그래프가 ROC(Receiver Operating Characteristic)이다!

true positive rate(the sensitivity) against the false positive rate(1-specificity )
즉 tpr(y축)은 민감 도기 때문에 실제 발생 중에 실제를 얼마냐 맞히냐?!
fpr(1-specificity)는 실제 발생하지 않은 것에서 발생했다고 예측하 것은 얼마냐!
이 2개는 trade off 관계를 가진다.
PRC Curve

Recall(Sensitivity) = TP / (TP + FN)
Precision = TP / (TP + FP)
그래프를 보면 알 듯이, Recall 실제 중에 실제를 맞힌 것을 높이면 높일수록,
Precision 실제 예측한 것 중에 실제일 확률이 점점 떨어지는 trade off 그림을 볼 수 있다.
Recall을 높이다 보면, Cut off를 굉장히 낮게 잡아야 할 것이고,
그러다 보면 실제 발생이 아닌 것을 발생이라 할 것이다.
그렇게 되면, 실제 예측한 것 중에 아닌 것으로 클래스가 들어가서 떨어지는 현상이 발생한다.
이처럼 어떤 관점에서 보는지에 따라, 모델을 보는 면이 달라지고, 의사결정도 달라져서
참 어렵다.
참고 :
https://towardsdatascience.com/hackcvilleds-4636c6c1ba53
Binary Classification Model Evaluation
A Guided Walkthrough
towardsdatascience.com
'ML(머신러닝) > BASIC' 카테고리의 다른 글
| MISSFOREST 알고리즘 설명 (0) | 2019.10.01 |
|---|---|
| 차원 축소에 대한 10가지 팁(Ten quick tips for effective dimensionality reduction) (0) | 2019.08.11 |
| 모델평가와 성능평가 _미완성 (0) | 2018.01.15 |
| 데이터 표현과 특성 공학 (0) | 2018.01.11 |
| 지도_비지도 요약 및 정리 (0) | 2018.01.09 |