지도 학습에 목적 함수로는 크게 2개로 나눌 수가 있다.
-
Regression
-
Classification
Objective Functions for Regression
keras에서는 많은 Regression에 대한 목적 함수를 제공하고 있다.

Regression 문제는 아래와 같이 D차원 공간 $R^D$의 독립 변수인 $x$와 종속 변수인 $y$ 사이에 선형 관계를 설정해야 한다.
2가지 관점에서 볼 수 있다.
- Ordinary Least Squares (uses Mean Squared Error, see above)
- Maximum Likelihood Estimation.
$$y_i(x_i,w)=w_0+w_1x_{i1}+w_2x_{i2}+...+w_Dx_{iD}+\epsilon_i, \text{ i=1,2,...N}$$
$$\epsilon_i \text{ is random error}$$
random error는 다음과 같은 원인 때문에 전제를 둬야 한다.
- wrong choice a linear relationship
- omission of one relevant independent variables
- measurement error
- instrumental variables — measured variables are proxies of “real” variables.
선형 회귀 분석의 목적은 모집단의 무작위 표본에서 $w$를 추정하는 것이다.
$$\hat{y_i}(x_i,\hat{w})=\hat{w_0}+\hat{w_1}x_{i1}+\hat{w_2}x_{i2}+...+\hat{w_D}x_{iD}, \text{ i=1,2,...N}$$
실제 종속 변수 $y_i$와 모델에서 추정한 종속 변수 $\hat{y_i}$에 차를 residual error라고 한다. $e_i=y_i-\hat{y_i}$
파라미터 $w$는 아래에 제시된 다양한 함수 형태 중에 하나를 목적 함수를 사용하여, 목적 함수를 최소함으로써, 추정된다.
Mean Squared Error

Mean Absolute Error
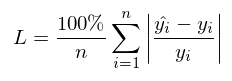
Mean Squared Logarithmic Error
MSE와 유사하지만, log scale로써 계산된다. 종속 변수는 음수가 아니어야 한다.
만약 종속 변수가 절대로 0이 아니라면 1을 추가해줄 수 있다.

Regularization
모델 복잡성과 제한된 데이터를 고려해서 과적합이 발생하지 않게 흔히 사용하는 방법은 정규화 텀을 추가하는 것이다.
정규화는 파라미터의 양을 조절하기 위해서 목적함수에 제한을 추가로 주는 것이다.
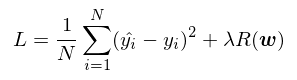
$R(W)$는 파라미터 w에 대해서 정규화 함수로 표현된다. $\lambda$는 하이퍼 파라미터로써, 정규화에 대한 강도를 조절한다고 할 수 있고, 이것은 튜닝할 부분이다.
Ridge Regression
목적 함수에 L2 norm 추가하는 것이다. 이것은 weight decay로 불리기도 한다.
학습은 가중치가 0 주변에 있기 만드는 효과가 있다.
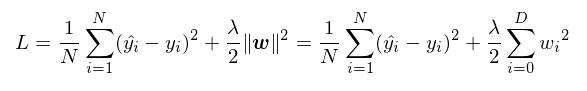
Lasso Regression
목적함수에 L1 norm을 추가하는 것이다. 이것은 모델을 sparse 하게 만든다. 즉 필요 없는 w는 0으로 만들어 사용하지 않게 된다.
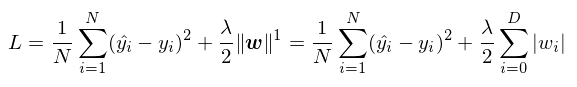
Elastic Regression
목적함수에 L1+L2 norm을 추가한 방법론이다. Elastic 방법론은 Ridge와 Lasso의 문제점을 해결하기 위해 고안되었다. 하지만 그렇다고 해서 항상 Ridge와 Lasso보다 좋다고는 할 수 없다.
$$L=\frac{1}{N}\sum_{i=1}^N(\hat(y_i)-y_i)^2+\frac{\lambda}{2}|w|^2+\frac{\lambda}{2}|w|^1$$

Objective Functions for Classification
regression에서는 종속 변수를 연속형 변수로 사용한 것과는 달리 classification 문제는 종속 변수를 classes를 다룬다. 그리고 각 클래스에 속하는 관찰 값의 확률을 추정하는데 초점을 맞춘다.
classification에서의 종속 변수는 이산형이나 다중 클래스라고 할 수 있다. $y$를 K개의 상호 배타적인 클래스의 그룹으로부터 class indicator가 되도록 한다. 즉 $y$는 $one-hot vecotr$로 나타낸다. $x$는 독립 변수라고 할 수 있다.
$$y=(y_1,y_2,...,y_K)^T \text{ such that } y_k \in {0,1} and \sum_k y_k =1$$
$$x=(x_1,...,x_D)^T \text{ is a D-dimensional vector } \in R^D$$
아이디어는 주어진 $x$와 파라미터 $w$로 나온 확률 함수 $y$의 클래스를 예측하는 확률 함수를 설계하는 것입니다.
이 K-dimensional Beroulli로써 확률을 표현하면 우리는 다음과 같이 표현할 수 있다.


위의 classification 문제를 풀기 위해서는 2가지 관점이 있다.
- Maximum Likelihood Estimation
- Cross Entropy
Maximum Likelihood Estimation
한 개의 관측치에 대한 K-dimensional Bernoulli는 전체 데이터셋으로 확장할 수 있다.
independent and identically distributed(iid) 데이터 점들(X, Y) 샘플에 대한 likelihood function은 다음과 같이 쓰인다.

이 우도 함수는 파라미터 $w$의 다양한 설정에 대해 관측된 표본 샘플 확률을 나타낸다.
빈도 주의자 패러다임에서, 파라미터 $w$는 표본 집합을 관측할 수 있는 가장 높은 확률을 산출하도록 추정된다. 즉 전체 결과는 바뀌지 않으므로 우도의 곱을 최대로 만드는 $w$와 그 우도 기댓값 $\sum_x P(y|x)logP(y|x;w)$를 최대로 하는 $w$가 같다고 할 수 있다.
The argmax does not change when we rescale the cost function, we can divide by the total number of data to obtain a version of the criterion that is expressed as an expectation with respect to the empirical distribution PdataPdata defined by the training data.
- Deep Learning Book 128page
파라미터 $w$ 설정에서의 우도 함수를 최대화하는 것은 음의 로그 우도(negative log-likelihood)가 단조롭게 감소하는 것을 최소화하는 것과 같다.

Cross entropy
분류 문제에 대한 접근을 information theory를 근간으로 한다. $Self-information$는 무작위 사건을 관찰함으로써, 놀라운 정도나 정보의 양을 측정한다. 그리고 그것은 사건의 확률을 기초로 한다.
보통 놀라움 정도나 정보의 양을 측정할 때 가능성이 높은 사건을 관찰하는 것보다 적게 관찰하는 것으로부터 정보를 더 많이 얻는다. 이는 $Self-information$은 확률 공간에 비해 단조 감소를 의미한다. 즉 예를 들어, 특정 박스에 파란 공만 있다고 했을 때, 이러한 경우에는 관찰할 수 있는 것이 파란 공만 된다. 이러한 경우 놀라움의 정도나 정보의 양인 entropy는 0이라고 할 수 있다.
정보 이론에서 정보의 정의는 $-log_2(p(x))$라고 하는 $h(x)$로 표현한다. log의 밑을 2로 하는 것은 Shanno 혹은 bit라고 한다. 머신 러닝에서는 주로 자연 상수를 밑으로 사용한다.
$$h(x)-log_2(p(x))$$
분포 p를 가진 H(x)로 표기되는 확률변수의 정보 엔트로피는 불확실성의 측정이고, Shannon entropy는 모든 사건 정보량의 기댓값을 말한다.
$$H(P)=H(x)=E_{x \sim p}[h(x)] = -E_{x \sim P} [logP(x)]$$
또한 K개의 클래스를 가진 경우 정보 엔트로피는 아래와 같이 표기할 수 있다.
$$H(x)=-\sum_{k=1}^K p(X=k)logP(X=k)$$
예를 들어, 가장 많이 드는 예시가 동전 던지기가 있다. $K=2$ 이런 경우 만약 불확실성을 가장 많이 가지게 한다고 생각했을 때, 동전의 앞면과 뒷면이 모두 50% 확률을 가지고 있으면, 불확실성이 가장 높다는 것을 직관적으로 알 수 있다.
$$P(X=1) = 0.5$$
$$P(X=0)=0.5$$
shannon entropy = $-[0.5log(0.5)+0.5log(0.5)] = -0.5*-0.69*2 = 0.69$
이것을 확률 값을 0에서 1 사이에서 계산을 하게 되면 다음과 같은 정보를 얻게 되고, 직관에서 알 수 있듯이 0.5에서 entropy를 가장 많이 얻을 수 있게 됩니다.

이 개념을 분류 문제로 확장하기 위해, 근사 확률을 사용하여 실제 확률을 근사화하는 것으로 한다고 하자.
$$y=(y_1, y_2,...,y_k)^T$$
$$\hat{y}=(\mu_1,\mu_2,...,\mu_k)^T$$

Cross entropy는 실제 확률 분포 $y$와 근사 확률 $\hat{y}$이 얼마나 가까운지를 측정한다.
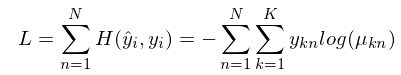
$$D_{KL}(y|\hat{y})=\sum_i y_i log(\frac{y_i}{\hat{y_i}})$$
$$= \sum_i(-y_ilog(\hat{y_i})+y_ilog(y_i)$$
$$=-\sum_iy_ilog(\hat{y_i})+ \sum_i y_i log(y_i)$$
$$=-\sum_iy_ilog(\hat{y_i})-\sum_i y_i log(\frac{1}{y_i})$$
$$=-\sum_i y_ilog(\hat{y_i})-H(y)$$
$$D_{KL}(y|\hat{y})=-\sum_i y_i log(\hat{y_i})-H(y)$$
즉 $D_{KL}$을 최소화하기 위해서는 $y$와$\hat{y}$에 대한 cross entropy와 $y$의 entropy의 차이를 줄여야 한다.
하지만 여기서 줄일 수 있는 값은 Cross entropy값이므로 $y$와 $\hat{y}$에 대해서 가까운 값을 만들어야 합니다. 즉, $y$와 $\hat{y}$의 분포를 가깝게 만들도록 해야 한다는 것을 의미한다.
negative log-likelihood를 쓰게 되면 몇 가지 이점이 생긴다고 한다.
만들려는 모델에 다양한 확률분포를 가정할 수 있게 되어, 유연하게 대응할 수 있다고 한다.
음의 로그 우도로 딥러닝 모델의 손실을 정의하면 이는 곧 두 확률분포 사이의 거리를 재는 함수인 cross entropy가 되며, 크로스 엔트로는 확률 분포의 종류를 특정하지 않기 때문입니다.
https://ratsgo.github.io/deep%20learning/2017/09/24/loss/
딥러닝 모델의 손실함수 · ratsgo's blog
이번 글에서는 딥러닝 모델의 손실함수에 대해 살펴보도록 하겠습니다. 이 글은 Ian Goodfellow 등이 집필한 Deep Learning Book과 위키피디아, 그리고 하용호 님의 자료를 참고해 제 나름대로 정리했음을 먼저 밝힙니다. 그럼 시작하겠습니다. 딥러닝 모델의 손실함수로 음의 로그우도(negative log-likelihood)가 쓰입니다. 어떤 이유에서일까요? 딥러닝 모델을 학습시키기 위해 최대우도추정(Maximum Likelihood Es
ratsgo.github.io
https://www.quantstart.com/articles/Maximum-Likelihood-Estimation-for-Linear-Regression/
Maximum Likelihood Estimation for Linear Regression | QuantStart
The purpose of this article series is to introduce a very familiar technique, Linear Regression, in a more rigourous mathematical setting under a probabilistic, supervised learning interpretation. This will allow us to understand the probability framework
www.quantstart.com
https://medium.com/@prakashpvss/cross-entropy-and-kl-divergence-178821a10f65
Cross Entropy and KL Divergence
If 1,2,….n represent a discrete set of possible events with probabilities p1,p2,….pn Shanon asked the following question
medium.com
'ML(머신러닝) > BASIC' 카테고리의 다른 글
| Measure Theory (Measureable space and Probability space) 공부해보기 (1) | 2021.05.29 |
|---|---|
| MISSFOREST 알고리즘 설명 (0) | 2019.10.01 |
| 차원 축소에 대한 10가지 팁(Ten quick tips for effective dimensionality reduction) (0) | 2019.08.11 |
| Binary Classification 중 주의해야 할 것과 팁 (0) | 2019.05.30 |
| 모델평가와 성능평가 _미완성 (0) | 2018.01.15 |