2018년도 자료 Prof. Jun Wang Computer Science, UCL에 있는 것을 기반으로 개인적인 이해를 위해서 정리를 해보고자 합니다...
2021.05.05 - [관심있는 주제/RL] - RL) MARL 설명 자료 -1 도입과 배경
2021.05.06 - [관심있는 주제/RL] - RL) MARL 설명 자료 -2 Stochastic Games

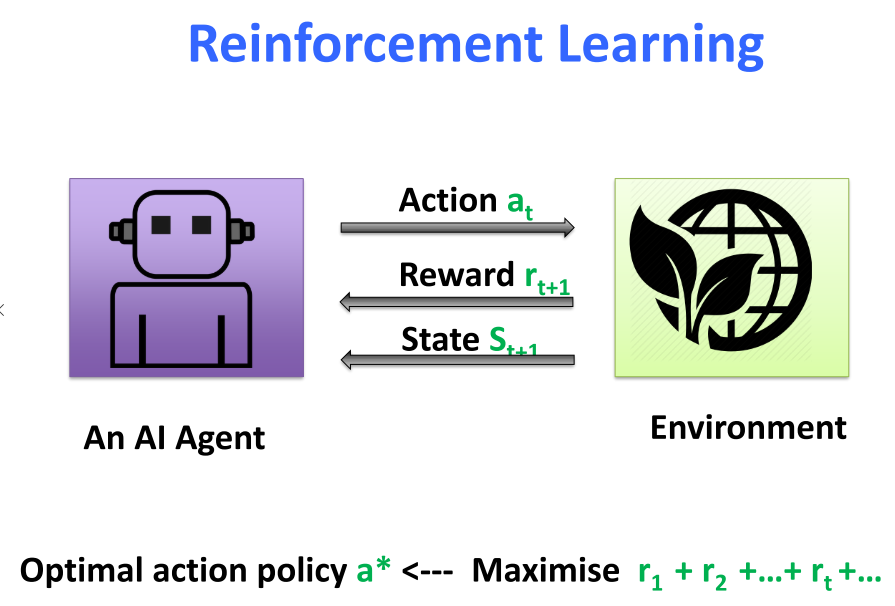

APPLICATION
- AI Plays Multiplayers Online Games
- Bidding Machine in Online Advertising
- Text Generation
Difficulty in Multi-agent Learning(MAL)
- MAL은 기본적으로 어려움
- 에이전트는 환경과 상호작용할 뿐만 아니라 다른 에이전트와도 상호작용해야 하기 때문
- 다른 에이전트를 환경의 일부로 고려하여 단일 에이전트 Q 학습을 사용하는 경우
- 이러한 세팅은 이론적인 수렴 보장을 깨고, 학습을 불안정하게 만듦
즉 하나의 에이전트의 전략의 변화는 다른 에이전트의 전략에 영향을 미치게 된다.
Sequential Decision Making

Markov Decision Processes (MDP)
- 의사결정자가 1개
- 다중 상태
Repeated Games
- 다중 의사결정자
- 하나의 상태( one normal form game )
Stochastic Games ( Markov Games)
- 다중 의사결정자
- 다중 상태 (multiple normal form games)
현재 우리가 다루고자 하는 것은 MARL은 Stochastic Games에 속한다.
즉 기존에 우리가 알고 있던 강화학습이 MDP를 기반으로 했다면, Multi agent는 좀 더 넓은 범위에서 Stochastic Games에 속하게 된다.
Recall: Markov Decision Processes
MDP는 단일 에이전트, 다중 상태 프레임워크이다.
MDP는 $(S,A,T,R)$ tuple이다.
- S는 States의 집합이다.
- A는 actions의 집합이다.
- T는 transition function $SxAxS -> [0,1]$
transition function은 상태와 액션의 함수로써 다음 상태에 대한 확률 분포이다. - R는 reward function $S x A -> R
reward function은 주어진 상태로부터 액션을 선택할 때 받은 보상을 정의한다.
MDP를 해결하는 것은 정책을 찾는 것으로 이루어져 있다. $\pi : S -> A$
- 할인 계수 γ로 할인된 미래 보상을 최대화하기 위해 상태를 행동에 매핑하는 것을 의미한다.

Recall: Matrix Games
Matrix Games는 multi agent(player), 단일 상태(single state)이다.
matrix game 또는 normal-form game은 튜플 상태이다. $(n, A_{1... n}, R_{1... n}$
- n은 플레이어의 수이다.
- $A_i$ 는 player i가 할 수 있는 액션의 집합이다.
(and A는 joint action space $A_1 x... x A_n$ - $R_i$는 player i의 payoff function이다 A -> R
플레이들은 가능한 액션 집합으로부터 액션들을 선택하고 모든 플레이어 액션에 의존하는 PAY OFF를 받는다.
이러한 것을 보통 matrix games이다. 왜냐하면 $R_i$ 함수들은 N 차원의 메트릭스들로 쓰여있다.
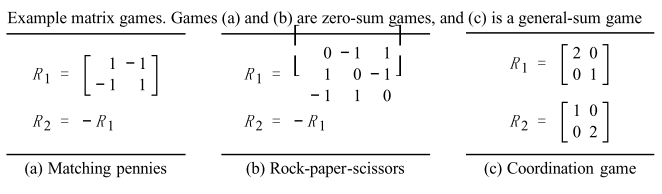

Matrix Game을 다음과 같이 크게 나눌 수 있다고 한다. 출동이 있는지 여부 / zero sum game 인지 general sum game인지 아니면 협력하는 게임인지 이것에 따라서 문제들에 따른 각각 예제들이 있는 것 같다.
죄수의 딜레마도 여기서 예를 들면 말하지 않을 때 둘 다 가장 큰 이득 보고 한명이 말하면 한쪽만 이득을 보는 문제도 이해관계가 충돌하는지 전체적인 이득의 합을 고려하는지 문제에 따라서 하나의 가지로 나온 것이다.
이처럼 에이전트가 많아질 경우에는 에이전트간의 관계 그리고 게임의 목적성에 따라서 문제를 푸는 형태가 바뀌어야 한다는 것을 알 수 있다.

일반적은 2x2 zero sum game 예시를 보면은 A라고 하는 매트릭스는 player 1에 대한 보상을 의미하고 그 반대 -A는 다른 플레이어의 보상이라고 하자.
각각의 플레이어를 위해서 게임의 가치를 찾고 최적의 전략을 최소 하나 이상을 찾을 수 있는 가에 대해서 물어보는 예제이다.
STEP 1, 순수한 전략으로 테스트를 해보기
STEP 2, 만약 잘안된다면, equalizing strategy를 찾음으로써 해결해보기 (내쉬 균형 방법론)
여기서 pure strategy란 게임 용어로써, 각 플레이어에게는 일련의 전략이 주어지며, 플레이어가 확률 1로 하나의 행동을 선택하면 해당 플레이어는 순수한 전략을 수행하는 것입니다.
이것은 개별 플레이어가 여러 행동에 대한 확률 분포를 선택하는 혼합 전략과 대조됩니다.
psychology.wikia.org/wiki/Pure_strategy#:~:text=A%20pure%20strategy%20is%20a, is%20playing%20a%20pure%20strategy.
STEP 1부터 봐보자.

만약 A가 B보다 크고, B가 C보다 작다면, B는 순수한 전략일 것이다
왜냐하면 B가 C보다 작기 때문에 C는 D보다 클 것이고, 아니면 C도 순수한 전략이 된다.
계속하게 되면 D는 A보다 작고 A는 B보다 작을 것이다.
NO pure strategy를 위해서는 다음과 같아야 한다
A가 B 이상이면, A> B <C> D <A 가 된다. 대칭적으로 A가 B이하이면 A <B> C <D> A
그래서 no pure strategy를 위해서는 다음과 같은 조건이 필요하다고 한다.
A> B , B <C, C> D 그리고 D <A
또는 A <B , B> C, C <D 그리고 D> A
이제 STEP 2를 살펴보자.

이제는 순수 전략이 아닌 MIXED 전략을 확률 기반으로 알아보게 되는 것이고 다음과 같은 수식을 얻는다고 한다.
아래 영상을 보면 mixed strategy에서 내쉬 균형을 사용하게 되면, 저 수식을 얻는 것 관련 영상자료가 있었다.
아마 이 부분을 이해하려면 게임이론에서 내쉬 균형이 어떻게 되는 지를 이해해야 저 수식을 알게 될 것이다.
참고
https://www.youtube.com/watch?v=7jBf5fzGBlk

그래서 저 수식을 기반으로 하게 되면 각 전략에 대한 optimal value를 알게 된다. 즉 각 플레이들이 얻는 보상에 따라서 각각의 전략의 최적 값을 구할 수 있다는 것인 것 같다.
Recall: Repeated Games
전형적인 반복된 게임들은 다음과 같다.
- 플레이어들은 normal-form game을 한다 (stage game)
- 그때 그들은 무엇이 발생하는지 이해하고 보상을 얻는다.
- 그들은 다시 게임을 한다.
- 기타..
즉 많은 시간 동안 유한하게 혹은 무한하게 반복된 게임을 하는 구조를 말하고 이러한 게임들은 다중 의사결정 자이지만 하나의 stage만 있는 경우이다.
이번 자료에서는 MAL에 대한 기본적인 자료에 대한 설명이 있었고, 다음 자료부터 Stochastic Games라는 자료를 소개하려고 합니다.
2021.05.05 - [관심있는 주제/RL] - RL) MARL 설명 자료 -1 도입과 배경
2021.05.06 - [관심있는 주제/RL] - RL) MARL 설명 자료 -2 Stochastic Games
wnzhang.net/tutorials/marl2018/index.html
SJTU MARL Tutorial 2018
SJTU Multi-Agent Reinforcement Learning Tutorial Jun Wang, Professor, UCL Email: j.wang [AT] cs.ucl.ac.uk Weinan Zhang, Assistant Professor, SJTU Email: wnzhang [AT] sjtu.edu.cn Oct. 14-15, 2018 Tutorial Slides pdf Lecture 1: Fundamentals of Reinforcemen
wnzhang.net
'관심있는 주제 > RL' 카테고리의 다른 글
| RL) Double DQN 알아보기 (0) | 2021.05.09 |
|---|---|
| RL) MARL 설명 자료 -2 Stochastic Games (0) | 2021.05.06 |
| Env) Multiagnet CityFlow 환경 (0) | 2021.05.05 |
| RL) Multi Agent RL 관련 자료 (0) | 2021.04.25 |
| RL) Mean Field Multi-Agent Reinforcement Learning 리뷰 (0) | 2021.04.23 |