특정 책에서 해당 논문에 대한 언급이 있고, 인용 수도 있는 것 같아서 리뷰해보려고 한다.
해당 논문을 통해서 MARL에 대한 이해도를 높여지길 기대한다.
해당 논문에서는 게임 이론을 적용하여 에이전틔의 정책 선택 문제를 해결하고 있다.
내쉬 균형 이론은 비협력적 게임에서 최적의 행동 정책을 찾기 위하여 중요하게 사용되는 것이고, 내쉬 균형에서 각 에이전트는 다른 에이전트의 행동이 주어졌을 때 다른 에이전트의 전략을 고려하여 최선의 선택을 하는 전략을 이용한다. 하지만 다수의 에이 전트 환경에서 고려할 상호작용의 수가 많아 내쉬 균형 전략을 찾기 어려운 문제가 있다
본 논문에서는 주변의 상호작용을 하나의 평균 상호 작용을 고려하여 문제의 복잡도를 줄인 다음 평균 상호 작용을 고려하여 문제의 복잡도를 줄인 다음 내쉬 평균을 찾는 MEAN FILED GAME이 도입되었다.
즉 하나의 에이전트는 자기 주변의 에이전트만을 고려하여 q 함수를 설계하고 학습의 타당성과 수렴성을 증명하였다고 합니다.

Abstract
에이전트의 수가 증가함에 따라서, 학습은 차원의 저주와 에이전트 상호작용의 지수적인 성장 때문에 다루기가 힘들다.
에이전트 모집단 내 상호 작용이 단일 에이전트와 전체 모집단 또는 인접 에이전트의 평균 효과 사이의 상호 작용으로 근사되는 Mean Field RL을 제시한다.
두 개체 간의 상호 작용이 상호 강화됩니다. 개별 에이전트의 최적 정책에 대한 학습은 모집단의 다이내믹에 따라 달라지는 반면 모집단의 다이내믹은 개별 정책의 집단 패턴에 따라 달라집니다.
실제 평균장 Q- 학습 및 평균 장 Actor-Critic 알고리즘을 개발하고 설루션의 내쉬 평형에 대한 수렴을 분석했다고 한다.
Gaussian squeeze, Ising 모델 및 전투 게임에 대한 실험은 평균 필드 접근 방식의 학습 효과를 정당화한다고 합니다.
또한 모델이 없는 강화 학습 방법을 통해 Ising 모델을 해결 한 첫 번째 결과를 보고해본다고 함.
1. Introduction
MARL은 공통 환경을 공유하는 일련의 자율 에이전트와 관련이 있습니다.
MARL에서 학습은 기본적으로 에이전트가 환경과 상호작용할 뿐만 아니라 서로와 상호작용하기 때문에 어렵다.
다른 에이전트를 환경의 일부로 간주하는 Independent Q-Laerning(Tan, 1993)은 다중 에이전트 설정이 이론적 수렴 보장을 깨고 학습을 불안정하게 만들기 때문에 종종 실패합니다.
왜냐하면 한 에이전트의 정책 변경은 다른 에이전트의 정책에 영향을 미치기 때문이죠
대신 다른 에이전트의 정책을 추측하여 추가 정보를 고려하는 것이 각 학습자에게 유익합니다.
연구에 따르면, joint action의 영향을 학습하는 에이전트는 협력 게임에 포함되는 많은 시나리오에서는 하지 못했던 성능을 보여줬다고 합니다.
cooperative games (Panait & Luke, 2005), zerosum stochastic games (Littman, 1994), and general-sum stochastic games (Littman, 2001; Hu &Wellman, 2003).
기존의 평형 해결 접근법은 원칙적이지만 소수의 에이전트만 해결할 수 있습니다.
(Hu &Wellman, 2003; Bowling & Veloso, 2002).
(Nash) 평형을 직접 해결하는 계산상의 복잡성으로 인해 대규모 그룹 또는 에이전트 집단이 있는 상황에 적용할 수 없습니다.
그러나 실제로는 대규모 멀티 플레이어 온라인 롤 플레잉 게임 (Jeong et al., 2015)의 게임 봇, 주식 시장의 거래 에이전트 (Troy, 1997)와 같이 많은 에이전트 간의 전략적 상호 작용이 필요한 경우가 많습니다. ) 또는 온라인 광고 입찰 에이전트 (Wang et al., 2017).
해당 논문에서는 많은 수의 에이전트가 공존하고 있을 때의 MARL을 다룹니다.
저자는 각각의 에이전트는 직접적으로 다른 에이전트들의 유한한 셋에서 상호작용하는 세팅을 고려한다.
직접적 상호작용의 체인을 통하여, 에이전트들의 어느 페어는 전역적으로 상호작용된다.
이 확장성은 Mean Field Theory를 평균장 이론을 사용하여 해결됩니다.
에이전트 모집단 내의 상호 작용은 전체 (지역) 모집단의 평균 효과를 사용하는 단일 에이전트의 상호 작용으로 근사됩니다. 학습은 여러 개체가 아닌 두 개체 간에 상호 강화됩니다.
개별 에이전트의 최적 정책에 대한 학습은 에이전트 모집단의 동적을 기반으로 하는 반면, 모집단의 동적은 개별 정책에 따라 업데이트됩니다.
이러한 형태를 기반으로, 실용적인 mean field Q-Learning와 mean field Actor Critic을 개발했다.
특정 조건 하에서 우리의 설루션이 수렴하는 것에 대해 논의했다.
간단한 다중 에이전트 리소스 할당에 대한 실험은 평균 필드 MARL이 다른 사람들이 실패할 때 다중 에이전트 상호 작용을 통해 학습할 수 있음을 보여줍니다.
또한 시간차 학습을 통해 MEAN FIELD MARL이 에너지 함수를 명시적으로 알지 못해도 Ising 모델을 학습하고 해결할 수 있음을 보여줍니다.
마침내 혼합된 협동 경쟁 전투 게임에서 MEAN FIELD MARL이 이전에 많은 에이전트 시스템에 대해 보고된 다른 기준에 비해 높은 승률을 달성했음을 보여줍니다.
2. Preliminary
MARL은 강화 학습과 게임 이론 사이에 교차합니다. 이 둘의 결합은 확률적 게임의 일반적인 틀을 낳는다
2.1. Stochastic Game
stochastic game에서 N개의 에이전트를 다음과 같이 구성할 수 있다.
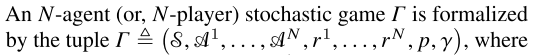
$S$ 는 state space $A^j$ 는 action space $j \in {1,2,... N}$ 각 에이전트의 리워드 함수는 다음과 같이 정의 된다.
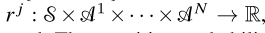
transition probability $p : S x A^1 x... x A^N$ -> $Q(S)$
$Q(S)$ 는 state space에 대해서 확률 분포 모음이 된다.
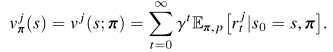

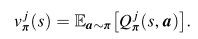
2.2. Nash Q-learning
MARL에서 각각의 에이전트의 목적 함수는 VALUE FUNCTION을 최대화하기 위해서 optimal policy를 학습하는 것이다.
각각의 에이전트 j에서 $v_{pi}^j$를 최대화하는 것은 모든 에이전트들의 joint policy $\pi$에 의존한다.
stochastic games에서 내쉬 균형의 개념은 중요하다.
이러한 가정을 만족한다 optimal policy일 경우 optimal policy가 아닌 경우보다 항상 가치 함수는 크거나 같다를 가정한다.


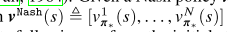


3. Mean Field MARL
joint action a의 차원은 에이전트 수에 따라서 기하급수적으로 증가한다.
모든 에이전트는 전략적으로 행동하고, 동시에 가치 함수를 평가할 때, 그것은 표준 q-function을 배우는 것은 어렵다.
pairwise local interactions를 사용하여 Q-function을 factorzie를 했다.

N(j)는 j 에이전트 주변 에이전트 set을 의미한다.
에이전트와 그 이웃의 쌍별 근사화는 에이전트 간의 상호 작용의 복잡성을 크게 줄이면서도 모든 에이전트 쌍 간의 글로벌 상호 작용을 암시적으로 보존한다는 점에 주목할 가치가 있습니다.
3.1. Mean Field Approximation

$a^j = [a^j_1, a^j_2,..., a^j_D]$
해당 수식은 테일러 급수 방정식을 이용해서 전개를 하다보면 아래와 같은 값이 나오게 된다. (mean filed-Q function)
$Q^j(s,a^j, \bar{a}^j)$
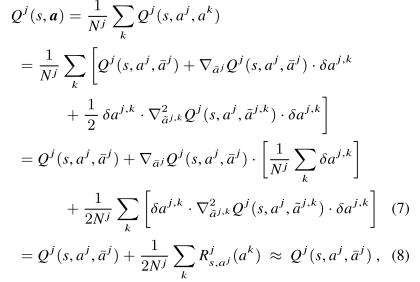

fig1에서 설명하듯이, mean field approximation과 함께 에이전트 j와 근처 에이전트 k 사이의 pairwise interactions $Q^j (s, a^j, a^k)$를 j와 중앙 에이전트(virtual mean agent) 사이에서 간단히 만들었다.
모든 근처의 j의 이웃들의 mean effect로서 virtual mean agent를 추상화했다.
$\bar{a}$는 agent j의 주변 에이전트들의 평균 액션을 의미함.
experience 같은 경우 $(s,{a^k},r^j , s^')$ 은 $(s,{\bar{a}^j+\sigma a^{j,k}},r^j , s^')$를 의미한다.
$a^j$는 onehot으로 인코딩 된 벡터를 의미한다. $a^j_1 , a^j_1 , a^j_2 , a^j_2, ...., a^j_D$
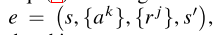
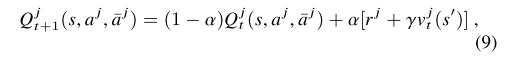

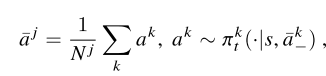
주변의 k개의 onehot encoding action의 평균을 이용하는 방식으로 가장 많은 경우가 나오는 액션에 더 가중치가 부여하는 방식으로 평균 액션을 가정했다. 즉 결과적으로 하나의 행동을 계산할 때 현재 J agent 의 주변 에이전트들에 따라서 변화할 수 있는 policy를 구성한 것이다.
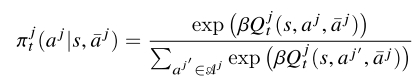
eq 11과 12를 iteration 함으로써, 모든 에이전트에서 평균 행동과 관련된 정책을 대안적으로 향상했다.
몇 번의 iteration을 통해서 mean action은 균형이 맞춰지고 policy는 수렴한다고 합니다.

3.2. Implementation

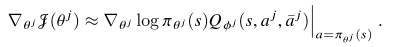
3.3. Proof of Convergence
해등 글에서는 컨셉만 확인하고 싶은 거니 증명은 나중에 시간이 될 때 하는 걸로..

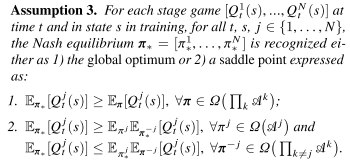
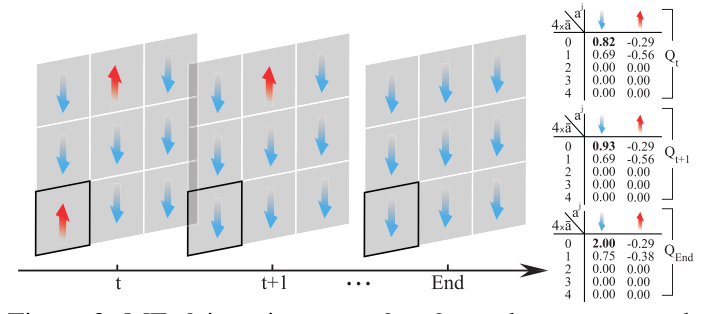
MF-Q iterations on 3x3 stateless 토이 예제다.
목표는 에이전트를 합의된 방향으로 조정하는 것입니다.
각각의 에이전트는 action들의 2가지 선택(up/ down)이다
같은 방향에서 각각의 에이전트가 머무르는 리워드 [0,1,2,3,4] 이웃들은 [-2.0, -1.0, 0.0 , 1.0 , 2.0] 있다.
하이라이트 된 에이전트 j에서 t+1의 보상은 2다 그리고 주변은 동시에 아래를 향한다.
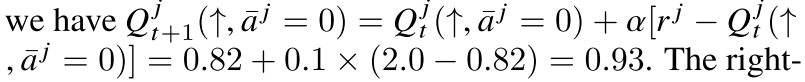
즉 이 위의 식을 일반화하면 아래와 같은 식이 나오게 된다.
TO BE.........
4. Related Work
5. Experiments
5.1. Gaussian Squeeze
5.2. Model-free MARL for Ising Model
5.3. Mixed Cooperative-Competitive Battle Game
6. Conclusions
개인적인 생각
관련 자료
www.koreascience.or.kr/article/JAKO202022663814865.pdf
'관심있는 주제 > RL' 카테고리의 다른 글
| Env) Multiagnet CityFlow 환경 (0) | 2021.05.05 |
|---|---|
| RL) Multi Agent RL 관련 자료 (0) | 2021.04.25 |
| RL) ETH Zurich & UC Berkeley Method Automates Deep Reward-Learning by Simulating the Past (2) | 2021.04.20 |
| RL) Deepmind Reward 관련 글 (EPIC WAY) (0) | 2021.04.20 |
| RL) REALab: Conceptualising the Tampering Problem 설명 (0) | 2021.04.20 |