https://towardsdatascience.com/how-exactly-umap-works-13e3040e1668
How Exactly UMAP Works
And why exactly it is better than tSNE
towardsdatascience.com
https://pair-code.github.io/understanding-umap/
Understanding UMAP
UMAP is a new dimensionality reduction technique that offers increased speed and better preservation of global structure.
pair-code.github.io
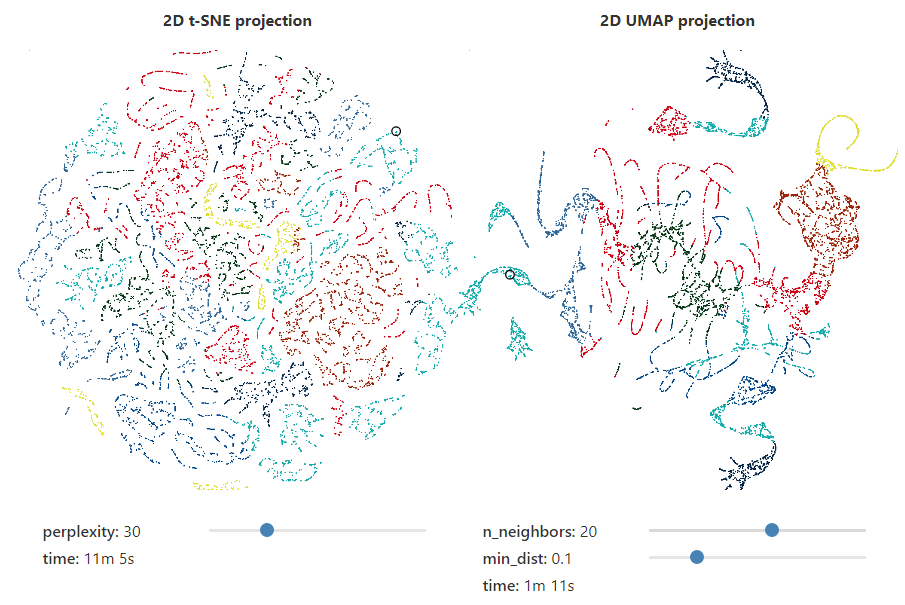
웬만하면 원문을 읽기를 추천
일단 글은 T-SNE을 비판하고 UMAP 최고이다라는 글이다.

TSNE를 수식으로 간단하게 설명하면 다음과 같다.

1) 고차원사이에서 관측거리를 확률로 정의하는 것 대칭성 룰 만족
2) Perplexity 식에서 최적의 \sigma 결정하는데 제한을 주는 개념 도입.
3) 저차원 임베딩의 포인트 페어들 사이에 거리를 student t 분포로 정의 / student t의 두꺼운 꼬리는 임베딩 할 때 저 차원에서 발생하는 crowding 문제를 극복할 수 있다 함. ( 먼가 느낌상 crowding problem은 꼬리가 두껍게 돼서 확률 값이 극단치에도 높게 하는데 이렇게 높게 함으로 통해 밀집되는 문제를 해결한다는 개인 느낌)
4) Eq. (4) Kullback-Libler 확산 손실 함수를 제공하여 고차원 확률을 저 차원 확률에 투영 그리고 gradient descent 최적화를 사용하여 gradient의 분석 가능한 형태로 제공

t-분포의 두꺼운 꼬리는 낮은 차원에서도 훨씬 더 멀리 떨어져 있도록 높은 차원에서도 포인트를 밀어낼 때 global distance information을 제공할 수 있다고 가정함
그러나 이러한 좋은 직관은 cost function(KL)의 선택에 의해 없어질 수 있다. 이유는 나중에...
라고 쓰여있다.
Key Differences Between tSNE and UMAP
글쓴이는 umap이 tsne이 와는 다르게 단단한 수학적인 원칙을 기반으로 한 차원 축소법이라고 말함.
나도 한번 umap 논문을 보려고 했지만, 너무 수학ㅓㄱ이라서 포기하고 떄려침....
그러나 https://umap-learn.readthedocs.io/en/latest/how_umap_works.html
이 도움이 많이 되었다고 함.
글쓴이도 처음에 umap이 그냥 단순히 tsne와 비슷한 neighbor graph라고 생각해서 당황했다 함.
논문을 보면 appendix c에서 차이에 대해 요약하려고 했지만. 크게 차이가 안보였다 함.
약간의 차이는 보았지만, 그것이 왜 그렇게 다른 결과를 내는지는 잘 모르겠다 함.
일단 차이점에 대한 설명 시작

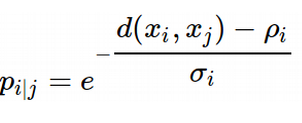
umap인 tnse와는 달리 euclidean distance를 꼭 쓰지 않고 고차원에서 지수 확률 분포를 사용 그리고 어떠한 거리도 다 연결해서 사용할 수 있다. 게다가 확률도 노말 라이즈 할 필요 없다.
여깃 ρ 는 중요한 파마 리터이다. 왜냐하면 저 ρ는 각각의 데이터 포인트 (i)로부터 첫 번째 이웃까지의 거리를 표현한다.
이것을 Manifold의 Local Connectivity를 확보할 수 있다 함. (잘 모르는 용어 나오기 시작..)
이것을 다시 말하면 각각의 데이터 포인트 대해 지역적으로 적응 형적은 지수 커널을 줄 수 있다 함.
아마 개인적인 생각은 보통 비모수에서 커널 밀도 함수 추정과 같이 거리를 잴 때 커널 함수를 이용해서 어떻게든 연결성을 유지한다는 것 같다.
The ρ parameter 은 umap 논문에서 Section 2와 Section 3 사이에서 유일한 다리 역할을 한다.
그렇지 않으면, 나는 퍼지 단순 집합 구성, 즉 섹션 2의 화려한 위상 데이터 분석이 3의 UMAP의 알고리즘 구현과 무슨 관련이 있는지 모르겠다. 퍼지 단순 집합이 결국 가장 가까운 이웃 그래프 구성으로 이어지는 것처럼 보이기 때문이다.
(갓 파파고)

UMAP은 고차원에서든 저 차원에서든 Normalization을 적용하지 않는다.
이것은 tsne와 다르고 꽤 기묘하게 보인다. 그러나 고차원이나 저 차원의 확률의 함수적인 형태는 이미 세그먼트에 대한 [0,1]이 스케일이 존재하고 분모에 Eq(1) 같은 normalization의 부재는 고차원 그래프에서 계산 시간을 줄여줄 수 있다.
이러한 것은 MCMC에서 Bayes'rule에 따라서 분모 쪽을 계산 안 하는 것과 같다고 생각하면 될 듯

UMAP은 Perplexity 대신에 근처 이웃의 수를 사용한다. UMAP은 근처 이웃의 수를 log2 function 없이 k개의 이웃의 수로 정의한다.

UMAP은 희미하게 고차원 확률 에어 다른 대칭성을 사용한다.
UMAP가 (매개 변수 ρ를 통해) 국지적으로 다른 측정지표를 가진 점을 함께 집중하게 한 후, A와 B 노드 사이의 그래프의 무게가 B와 A 노드 사이의 무게와 같지 않을 수 있으므로 심층화가 필요하다. 왜 정확히 UMAP가 tSNE가 사용하는 대칭 대신에 이런 종류의 대칭성을 사용하는지는 명확하지 않다고 한다.
내가 다음 포스트에서 보여줄 (UMAP를 처음부터 프로그래밍하는) 다른 대칭 법칙에 대한 나의 실험은 이것이 마지막 저 차원 구현에 사소한 영향을 미칠 만큼 중요한 단계라는 것을 납득시키지 못했다


plt.figure(figsize=(20, 15))
y = np.linspace(0, 10, 1000)
my_prob = lambda y, a, b: np.power(1 + a*y**(2*b), -1)
plt.plot(y, my_prob(y, a = 1, b = 1))
plt.plot(y, my_prob(y, a = 1.93, b = 0.79))
plt.plot(y, my_prob(y, a = 1.93, b = 5))
plt.gca().legend(('a = 1, b = 1', 'a = 1.93, b = 0.79', 'a = 1.93, b = 5'), fontsize = 20)
plt.title("Low-Dimensional Probability of Pairwise Euclidean Distances", fontsize = 20)
plt.xlabel("Y", fontsize = 20); plt.ylabel("Q(Y)", fontsize = 20)
plt.show()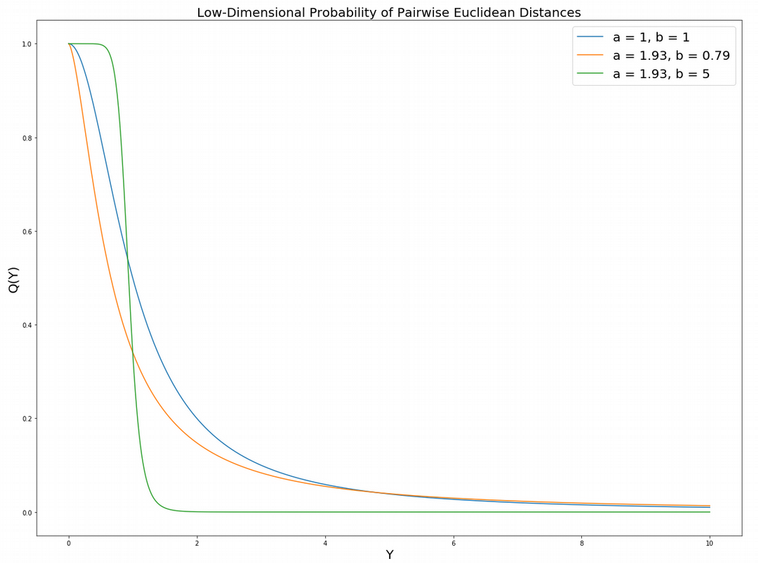
그림에서 알 수 있듯이 family of curves는 파라미터 b에 굉장히 민감하다.
b가 클수록 작은 Y에 대해서 높고 평평함을 유지하고 꽤 연결이 tigthly 하게 되어 있다.
Q(Y) function behaves almost like a Heaviside step(계단 함수)?
UMAP는 저 차원 공간에서 서로 가까운 모든 점에 대해 거의 동일한 저차원 좌표를 할당한다.
min_dist는 UMAP 치수 감소 그림에서 종종 관찰되는 초밀도 클러스터로 이어지게 한다.
a, b 파라미터를 설명하기 위해서 간단한 piecewise 함수를 보여준다고 함.
from scipy import optimize
import matplotlib.pyplot as plt
import numpy as np
MIN_DIST = 1
x = np.linspace(0, 10, 300)
def f(x, min_dist):
y = []
for i in range(len(x)):
if(x[i] <= min_dist):
y.append(1)
else:
y.append(np.exp(- x[i] + min_dist))
return y
dist_low_dim = lambda x, a, b: 1 / (1 + a*x**(2*b))
p , _ = optimize.curve_fit(dist_low_dim, x, f(x, MIN_DIST))
print(p)
plt.figure(figsize=(20,15))
plt.plot(x, f(x, MIN_DIST), "o")
plt.plot(x, dist_low_dim(x, p[0], p[1]), c = "red")
plt.title("Non-Linear Least Square Fit of Piecewise Function", fontsize = 20)
plt.gca().legend(('Original', 'Fit'), fontsize = 20)
plt.xlabel("X", fontsize = 20)
plt.ylabel("Y", fontsize = 20)
plt.show()
view rawOptimize_StudentDistr.py hosted with ❤ by GitHub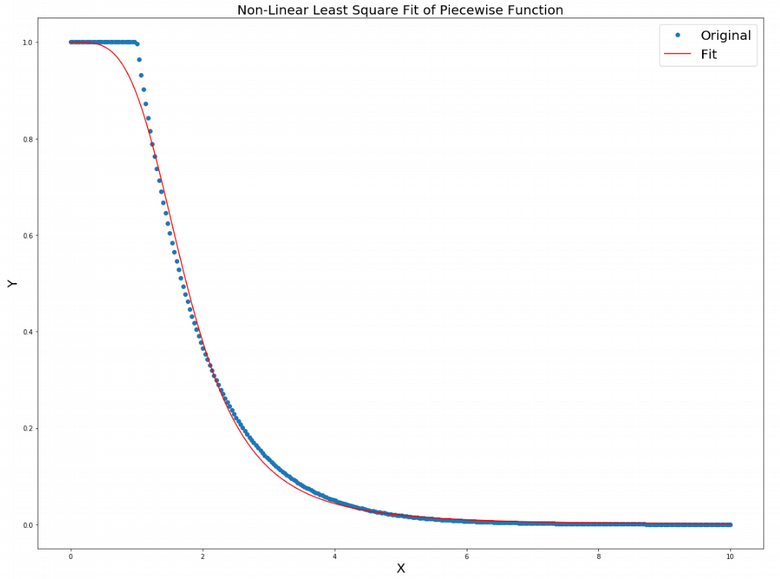
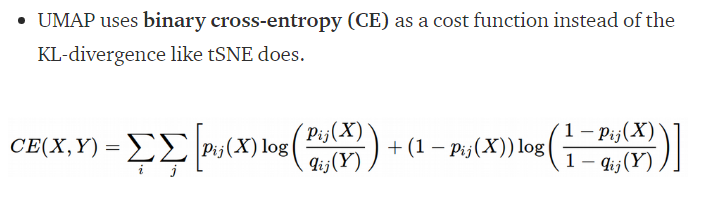
UMAP은 TSNE과는 다르게 Cross Entropy를 사용한다고 함. 저 식에서 2번째 텀이 왜 UMAP이 Global data structure를 잘 캐치하게 되는지에 대해서 보여주겠다고 함. (지역 구조를 중간 정도의 난해한 값으로 모델링할 수 있는 tSNE와는 대조적이다.)
일단 cross entropy의 gradient descent에 대해 알 필요가 있다고 함.


UMAP은 초기에 TSNE가 사용한 RANDOM NORMAL INTIALIZATION 과는 달리 Graph Laplacian을 사용한 저 차원 coordinates를 할당함. 그러나, 이것은 최종 저 차원 표현에 사소한 영향을 주어야 한다, 이것은 적어도 tSNE의 경우였다.
그러나, 이것은 UMAP이 더 이상 무작위 초기화가 아니기 때문에 실행에서 실행으로 변경되는 것을 줄여줄 것이다.
(너무 어렵..)
The choice of doing initialization through Graph Laplacian is motivated by the interesting hypothesis of Linderman and Steinerberger who suggested that minimization of KL-divergence in the initial stage of tSNE with early exaggeration is equivalent to constructing the Graph Laplacian.
Graph Laplacian, Spectral Clustering, Laplacian Eignemaps, Diffusion Maps, Spectral Embedding, etc. refer to practically the same interesting methodology that combines Matrix Factorization and Neighbor Graph approaches to the dimension reduction problem.
사실 잘 모르겠고 결국 Graph Laplician 썼는데 저 차원 방법에서 쓰는 방법이다(이런 느낌?..)
초기에 low dimensional coordinates를 보여준다 함(spetralembedding 함수 사용) (cafs 데이터 사용)
from sklearn.manifold import SpectralEmbedding
model = SpectralEmbedding(n_components = 2, n_neighbors = 50)
se = model.fit_transform(np.log(X_train + 1))
plt.figure(figsize=(20,15))
plt.scatter(se[:, 0], se[:, 1], c = y_train.astype(int), cmap = 'tab10', s = 50)
plt.title('Laplacian Eigenmap', fontsize = 20)
plt.xlabel("LAP1", fontsize = 20)
plt.ylabel("LAP2", fontsize = 20)
plt.show()

위에선 결국 UMAP 이 TSNE와의 차이점을 설명하고 있고, 개인적으로 생각할 때 중요하다 생각하는 것은 Loss function 하고 다양한 거리 함수를 쓸 수 있고, 다른 대칭성 규칙 사용?
Why tSNE Preserves Only Local Structure?
일단 첫 번째 we have the σ parameter in the Eq. (1)에서 이 매개변수는 데이터가 서로 "감각"하는 방법을 설정한다.
쌍방향 유클리드 거리의 확률은 기하급수적으로 감소하며, σ의 작은 값에서 기본적으로 원거리 지점(큰 X)의 경우 0이며, 가장 가까운 이웃(작은 X)에 대해서만 매우 빠르게 성장한다.
바로 큰 large σ 에서는 먼 거리와 가까운 점들의 확률들이 유사해진다. 그 확률은 모든 거리에서 1이 되게 된다.
plt.figure(figsize=(20, 15))
x = np.linspace(0, 10, 1000)
sigma_list = [0.1, 1, 5, 10]
for sigma in sigma_list:
my_prob = lambda x: np.exp(-x**2 / (2*sigma**2))
plt.plot(x, my_prob(x))
plt.gca().legend(('$\sigma$ = 0.1','$\sigma$ = 1', '$\sigma$ = 5', '$\sigma$ = 10'),
fontsize = 20)
plt.title("High-Dimensional Probability of Pairwise Euclidean Distances", fontsize = 20)
plt.xlabel("X", fontsize = 20); plt.ylabel("P(X)", fontsize = 20)
plt.show()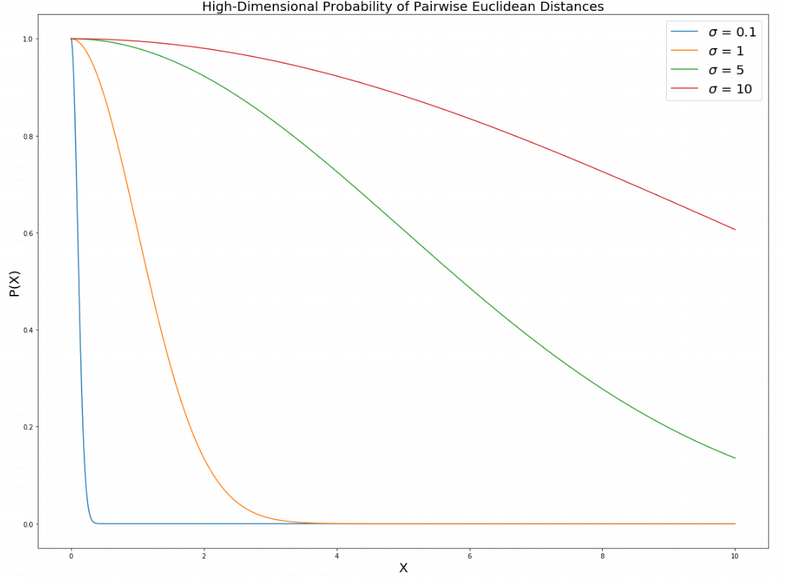
큰 값을 가질수록 대부분의 확률 값이 1에 가까워지는 것을 확인할 수 있는 그림
흥미롭게도 만약 고차원에서 테일러급수로 쌍별로 유클리디안 거리의 확률 확장한다면 멱 법칙에 근사한다고 함
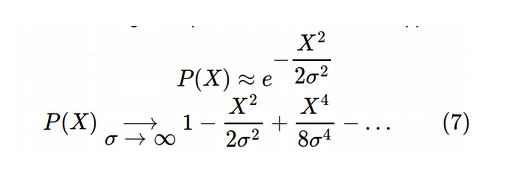
쌍별로 유클리디안 거리들에 대한 멱법칙은 Multi Dimensional Scaling(MDS)의 Cost function과 유사해진다고 함.
이것은 그들이 서로 가깝든지 물들지 상관없이 점들의 각각의 페어 사이의 거리를 보존하려고 노력하는 global distance를 보전하기로 알려져 있다.
대규모 σ tSNE는 데이터 지점들 간의 장거리 상호작용을 설명하므로 tSNE가 국지적인 거리만 다룰 수 있다고 말하는 것이 전적으로 옳은 것은 아니다. 그러나 우리는 전형적으로 우리 스스로를 perplexity의 유한한 값에 의해서 제한한다.
어떤 사람은 Perplexity를 5~50 사이를 추천한다고 한다. 실제로 좋은 구성의 root(N)이 local과 global information에서 좋은 절충안이 된다고 한다. 반대로 , σ → 0, 제한하면 극단적인 locality를 가지게 된다고 한다. 이것은 dirac delte function과 유사하다고 한다.

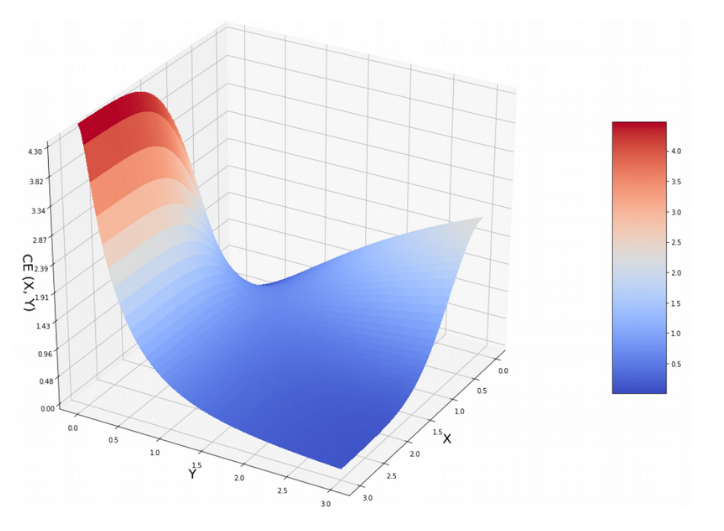
보면 큰 특이점은 KL은 큰 X 값에서 Y가 높던 작던 Cost가 낮지만 CE 같은 경우에는 큰 페널티를 준다.
이것이 Global distance로 가게 잘한다고 함


결국 이 글은 umap이 훨씬 좋고 중요한 것은 Cross Entropy Cost function을 통해서 Global Structure를 보장한다는 점이다. 그리고 아래 글에서는 머 속도면에서 훨씬 빠르다. (그건 아래 글을 더 읽어보면...ㅠ)
https://towardsdatascience.com/how-exactly-umap-works-13e3040e1668
How Exactly UMAP Works
And why exactly it is better than tSNE
towardsdatascience.com
'관심있는 주제' 카테고리의 다른 글
| 딥 러닝 BN / LN / WN의 정규화 설명 - 추천 자료 (0) | 2019.11.10 |
|---|---|
| Self Normalizing Neural Network (Fully Connected Layer 의 희망?) (0) | 2019.11.09 |
| Scipy에서 제공하는 분포간 거리 함수(Statistical Distance)와 차이점. (2) | 2019.06.08 |
| Uncertainty Autoencoders: Learning Compressed Representations via Variational Information Maximization - 리뷰 (0) | 2019.06.05 |
| LSTM AutoEncoder를 사용해서 희귀케이스 잡아내기 (5) | 2019.05.23 |