Scipy에서 제공하는 분포간 거리 함수(Statistical Distance)와 차이점.

우연히 유튜브에서 추천해준 2018 Detecting Anomalies Using Statistical Distances 이 

내가 관심이 있는 Anomaly detection과 Statistica Distance라서 듣게 되었고, 좋은 것을 많이 얻어서 공유합니다.

 

단순히 평균만 비교하게 되면 비교를 하기 어렵다는 예시

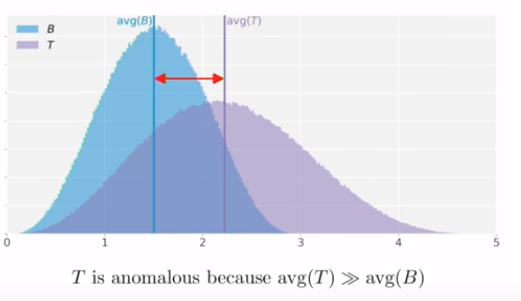
그렇다면 Quantile로 하면 되지 않느냐?

quantile 만 비교를 하게 되도 거리간 개념을 잴 때 문제가 발생

이렇게 간단한 통계량 값만 이용해서는 충분하지 못하다.

그러므로 이런 통계량 값들을 결합해서 사용하거나, 통계적 거리를 사용해야 한다.

 

Statistical Distance

Kolmogorov-Smirnov Distance

 

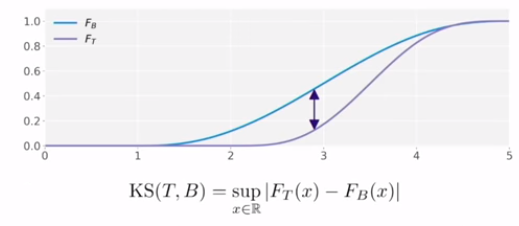
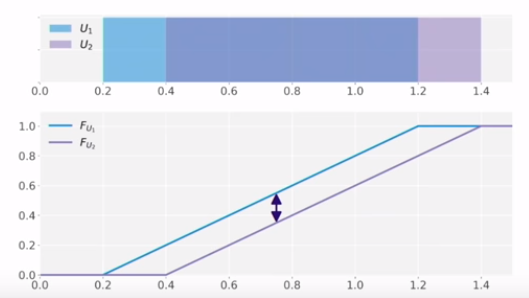
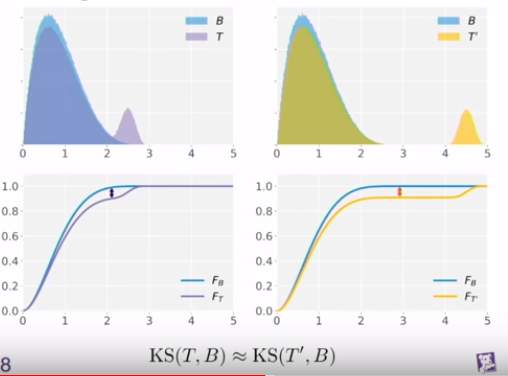
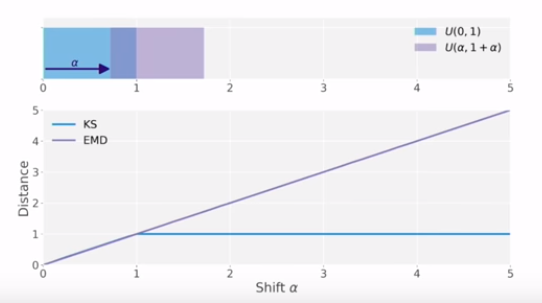
하지만 약간 기존 family가 아닌 쌍봉 같은 경우가 나오는 경우 KS로 거리를 재게 되면, 다음과 같은 문제가 생긴다. 

멀리 떨어져있어도 거의 같은 값으로 표현이 된다.

그래서 올바른 방법은 저만큼 차이 나는 것을 표현하는 거리 함수를 써야 할 것 같다.

 

 Earth Mover's distance

KS 보다 더 민감하게 계산이 가능하다.

EM distance를 누적 분포 형태로 표현이 가능하게해서 계산이 쉽게 할 수 있다는 것을 발견함.

 

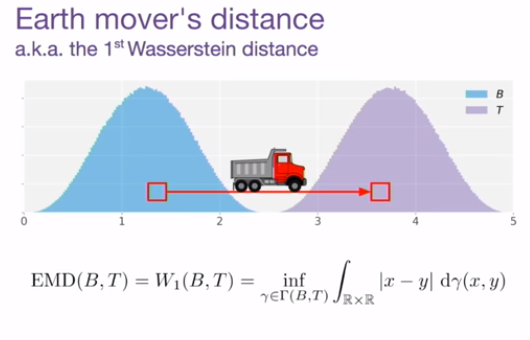
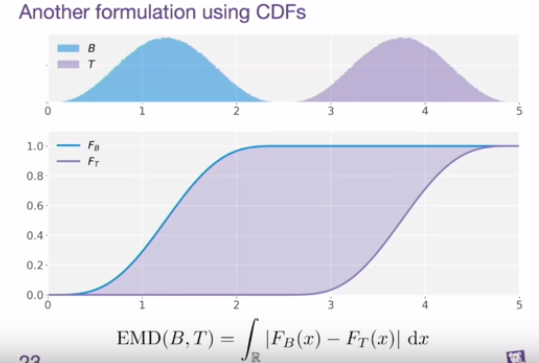
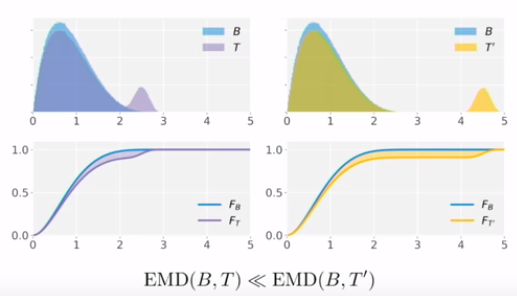
실제로 기존의 KS에서는 두 분포를 같은 값으로 제시했지만, 여기서는 더 멀리 있는 분포라는 표현을 할 수 있게 됨.

 

Cramer-von Mises distance

 

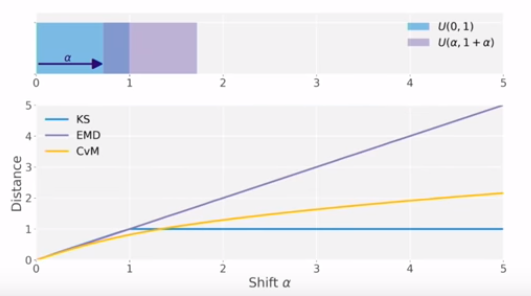
CvM 같은 경우 너무 멀리 떨어져 있어도 너무 큰 제약을 주지 않게 되는 효과를 가지게 된다.

 

 

결론

최근에 분포간 거리를 재는 것에 대해서 관심을 가지고 있게 되고, 다 어디서 들어봤지만, 먼가 명확히 정리해준 것 같아서 좋았고, 실제로 ks로 비교하고 있었는데, wassernstein distance 나 cramer distance를 제공하기 때문에 사용하면 더 엄밀하게 분포 간 비교를 하는데 활용할 수 있을 것 같다.

 

 

KSkolmogorov-smirnov

https://docs.scipy.org/doc/scipy-0.15.1/reference/generated/scipy.stats.ks_2samp.html

scipy.stats.ks_2samp — SciPy v0.15.1 Reference Guide

Wasserstein Distance

• WGAN

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.wasserstein_distance.html

scipy.stats.wasserstein_distance — SciPy v1.3.0 Reference Guide

 

Crammer Distance

• Cramer gan

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.energy_distance.html

scipy.stats.energy_distance — SciPy v1.3.0 Reference Guide

 

https://www.youtube.com/watch?v=U7xdiGc7IRU&feature=youtu.be

 

끝