저번에는 UMAP 실습 코드를 공유했는데, 이번에는 어떻게 작동하는지에 대해서,
공부해야 할 필요성이 생겨서 글을 남기면서 공부하려고 한다.
https://data-newbie.tistory.com/134?category=687142
UMAP (Uniform Manifold Approximation and Projection)
이것의 관심을 가진 이유는 원래 기본적인 T-SNE은 Visualization 용으로만 쓰는데, 실제로 이 패키지에서는 그 Embedding 한 것을 변수로 사용할 수 있다고 합니다. 그래서 train을 학습시켜서 그걸 다시 test에..
data-newbie.tistory.com
https://umap-learn.readthedocs.io/en/latest/how_umap_works.html
How UMAP Works — umap 0.3 documentation
How UMAP Works UMAP is an algorithm for dimension reduction based on manifold learning techniques and ideas from topological data analysis. It provides a very general framework for approaching manifold learning and dimension reduction, but can also provide
umap-learn.readthedocs.io
umap 과 t-sne의 차이를 볼 수 있는 글은 다음 글을 참고하면 됩니다.
https://data-newbie.tistory.com/295
UMAP이 T-SNE와 다른점에 대한 글 리뷰
https://towardsdatascience.com/how-exactly-umap-works-13e3040e1668 How Exactly UMAP Works And why exactly it is better than tSNE towardsdatascience.com https://pair-code.github.io/understanding-umap..
data-newbie.tistory.com
UMAP은 topological data 분석으로 아이디어와 manifold learning 기술을 기반으로 한 차원 축소 알고리즘입니다.
결국 크게 알아야 할 것은
- topological data analysis
- manifold learning
기본 수학 지식으론 다음이 필요하다고 합니다.
- algebraic topology
- topological data analysis
다음 단계론 실제 데이터를 topological data analysis algorithm의 기본 가정에 더 가깝게 하기 위해 Riemannian Geometry을 사용합니다.
불행하게도, 이러한 방법은 새로운 문제를 초래하지만, 심화된 수학과 Fuzzy Logic을 이용해 해결했다고 합니다.
여러 가지 조각나는 것을 다시 결합하는 방식으로 저차원 representation을 찾는 새로운 접근 방식
퍼지 논리(Fuzzy Logic)이란, 퍼지 이론의 특정한 명시를 이해하고 조정하기 위한 수학적 기술로서 Linguistic variable을 다루기 위한 수학적인 도구를 제공하기 위함
자연 언어 등의 애매함을 정량적으로 표현하기 위하여 1965년 미국 버클리대학교의 L. A. 자데(Zadeh) 교수에 의해 도입된 퍼지 집합의 사고방식을 기초
퍼지의 원리는 모든 것이 정도의 문제라고 주장한다. 퍼지 성은 둘 또는 그 이상 아마도 무한한 선택의 여지가 있는 스펙트럼을 의미한다. 퍼지 성은 2진법이 아니라 흑과 백 사이의 무한한 회색의 농도인 아날로그를 의미한다.
즉 1+1=2가아니라는 뜻이다.
확률론과의 차이
퍼지 이론은 확률 이론과 근본적으로 다르다. 어떤 사람이 부엌과 침실 사이의 문간에 서 있다고 할 때, "그 사람은 50% 부엌, 50% 침실에 서 있다"라고 말하는 것과 "그 사람은 50%의 확률로 부엌에 있거나 50% 확률로 침실에 있다"라고 말하는 것은 다르다.
퍼지 이론은 "회색 이론"이라는 별명으로도 불린다. 왜냐하면 흑백 사이의 수많은 회색을 상정하기 때문이다. 그리고 이 개념을 표현하는 방식으로 "매우", "조금", "약간", "보통의"라는 언어적 형용사를 사용한다. 그렇기 때문에 퍼지 이론을 "비수 학적"이라고 생각하는 사람도 있다.
Topological Data Analysis and Simplicial Complexes
Simplicial complexes are a means to construct topological spaces out of simple combinatorial components.
단순한 복합체는 단순한 조합 구성 요소에서 위상 공간을 구성하는 수단입니다.
이를 통해 토폴로지 공간의 연속적인 형상을 처리하는 복잡성을 상대적으로 간단한 조합 및 계산 작업으로 줄일 수 있습니다.
Geometry와 Topology를 길들인 방법은 일반적으로 Topology 데이터 분석과 특히 차원 축소에 대한 우리의 접근 방식의 기본입니다.
첫 단계는 simplices라 불리는 간단한 결합의 Building blocks을 제공하는 것입니다.
a simplex is a very simple way to build an k-dimensional object. A kk dimensional simplex is called a kk-simplex, and it is formed by taking the convex hull of k+1k+1 independent points.

사실 머라는지는 잘 모르겠고, 결국 거절을 여러 개로 합친 Simplicial complex라는 복합체로써 만든다고 합니다.
토폴로지에서 유한 데이터 집합에이 이론적 도구를 어떻게 적용합니까?
The key is that the background topological theory actually provides guarantees about how well this simple process can produce something that represents the topological space itself in a meaningful way (the Nerve theorem is the relevant result for those interested).
위에는 전혀 뭐라는건지 모르겠다........
실제 적용은 어떻게??
데이터 샘플이 기본 토폴로지 공간에서 추출되었다고 가정하면 해당 공간의 토폴로지에 대해 알기 위해 공개 샘플을 생성해야 합니다.
데이터가 실제로 Metric space에 있는 경우 (즉, 점 사이의 거리를 측정할 수 있는 경우), Open Cover를 근사화하는 한 가지 방법은 각 데이터 점에 대해 고정된 반경의 공을 간단히 만드는 것입니다.
토폴로지 공간 자체가 아닌 유한 샘플만 가지고 있기 때문에 우리는 그것이 진정한 오픈 커버인지는 확신할 수 없지만 합리적으로 기대할 수 있는 근삿값이 될 수 있습니다.
이 접근법은 또한 커버와 관련된 Čech 콤플렉스가 각 데이터 포인트에 대해 0-simplex를 갖게 된다는 장점이 있습니다.

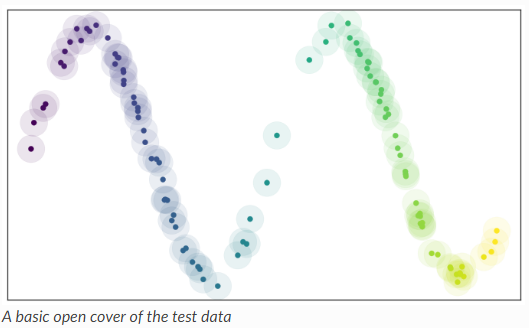

맨 왼쪽은 sample이 유한한 상태인 현재 상태를 보여준 것이고, 중간에는 radius를 고정시켜서 원의 커버를 그린 것이다. 그리고 마지막에는 이것을 포인트처럼 0, 1 ,2 simplices as 점 , 선 , 삼각형으로 묘사한 것이다.
즉 여러 개로 합친 Simplicial complex라는 복합체로써 만든다고 합니다.
- simplicial complex does a reasonable job of starting to capture the fundamental topology of the dataset;
- most of the work is really done by the 0- and 1-simplices, which are easier to deal with computationally (it is just a graph, in the nodes and edges sense).
따라서 만약 우리가 topological representation을 얻는 방법에 적용하면 낮은 차원에서 표현하는 차원 축소에 활용할 수 있다. 만약 0 , 1 simplices를 활용하면 그래프처럼 표현할 수 이싿고 한다.
즉 결국에는 단순한 데이터에 이웃을 만들고 그 그래프를 배열하는 것입니다.
이렇게 하는 데에는 여러 가지 이유가 있다고 하는데요.
- 추상적일지라도, 이론적인 정당성을 제공하는 topological approach를 사용했습니다.
- 우리가 접근법을 일반화하고 위에 설명된 알고리즘의 종류의 어려움을 해결할 수 있게 하는 것이 보다 추상적인 토폴로지 방식이라는 것입니다
수학 베이스가 너무 딸려서 하나도 모르겠네요 ㅠㅠ
결론적으로 간단하게 말하자면,
그때 가까운 데이터들끼리 이어줄 때, Simplices 방법을 사용하고, clustering을 하겠다는 것 같습니다.
여기서의 정당성은 topological representation하게 할 수 있다라는 것 같습니다.
2에서는 밑에 있는 내용을 좀 더 볼 예정입니다.
아직 그러고보니, UMAP에서 Uniform 이야기는 안나왔네요!
더 기술적인 것을 알고 싶다면 여기로 가라고 합니다...( 일단 자신이 없으니 논문은 일단 패스합니다.)
https://arxiv.org/abs/1802.03426
UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction
UMAP (Uniform Manifold Approximation and Projection) is a novel manifold learning technique for dimension reduction. UMAP is constructed from a theoretical framework based in Riemannian geometry and algebraic topology. The result is a practical scalable al
arxiv.org
'관심있는 주제 > Dimension Reduction' 카테고리의 다른 글
| Why You Should Always Use Feature Embeddings With Structured Datasets - 리뷰 (0) | 2021.02.28 |
|---|---|
| 여러가지 구조의 Autoencoders (0) | 2019.06.13 |
| UMAP은 어떻게 작동할까? (Uniform Manifold Approximation and Projection) - 3 (0) | 2019.06.08 |
| UMAP은 어떻게 작동할까? (Uniform Manifold Approximation and Projection) - 2 (0) | 2019.06.06 |