https://data-newbie.tistory.com/171
UMAP은 어떻게 작동할까? (Uniform Manifold Approximation and Projection) - 2
https://data-newbie.tistory.com/169 UMAP은 어떻게 작동할까? (Uniform Manifold Approximation and Projection) - 1 저번에는 UMAP 실습 코드를 공유했는데, 이번에는 어떻게 작동하는지에 대해서, 공부해야 할..
data-newbie.tistory.com
Finding a Low Dimensional Representation
그냥 사용만 하면 마음이 편한데, 알려고 하니 너무 어렵네요
예를 들면 통상적인 숫자 2 나 3에 퍼지의 사고방식을 도입하면 '거의' 2 나 '대체로' 3이라고 하듯이 퍼지 한 수(fuzzy number)가 된다. 그렇게 하여 퍼지연산 이 만들어진다.
마찬가지로 적분은 퍼지 적분으로 되고 토폴로지라고 하는 수학의 분야에서는 fuzzy toplogy라고 하는 새로운 수학이 생겨나게 되는 것이다.
먼가 이 저자들도 대략적인 대테러의 유사한 구조를 만들면서 lowdimensional representation을 원한다고 합니다.
두 가지 의문이 들 수 있는데요.
- 어떻게 lowdimensional representation의 fuzzy topological 구조를 결정하는지?
- 어떻게 좋은 것을 찾을 수 있는지?
첫 번째 답은
이미 이전에 설명한 것으로 거의 답이 나왔다고 합니다.
아마도 데이터의 퍼지 위상 구조를 찾기 위해 사용했던 것과 동일한 절차를 따라야 합니다.
하지만 이렇게 하다 보면 단점은, 데이터 주위에 일부 manifold에 놓이지 않고 매우 특정한 manifold에 놓여있는 lowdimensional representation이 될 거라고 합니다.
물론 그 manifold는 우리가 low dimensional eculidean space에 embedding 하려고 한 것입니다.
그래서 이것은 우리가 이전에 갔던 모든 노력이 저 차원 표현으로 작업할 때 매니 폴드를 가로지르는 거리의 개념을 다양하게 바꾼다는 것을 의미합니다.
다른 단점은 우리가 가장 가까운 이웃에 대한 거리를 사용했다는 것입니다. 그리고 주어진 데이터를 통해 계산한다는 것입니다. 이것은 또한 우리가 좋은 저 차원 표현으로 최적화할 때 매니 폴드에서 전역 적으로 사실이 되고 싶어 하는 속성이기 때문에 이를 알고리즘의 하이퍼 파라미터 min_dist로 조정을 해야 하는 부분입니다.
두 번째 질문은 '우리가 어떻게 좋은 저 차원 표현을 발견할 수 있는가?'라는 질문은 퍼지 위상 구조의 관점에서 우리가 얼마나 근접한 일치를 측정했는지 측정할 수 있는 능력에 달려있다.
이러한 측정을 통해 우리는 이것을 가장 가까운 퍼지 위상 구조로 낮은 차원 표현을 찾는 최적화 문제로 바꿀 수 있습니다.
물론 우리의 친밀도 측정에 다양한 특성이 있는 것으로 밝혀지면 적용할 수 있는 최적화 기법의 성격이 달라집니다
여기서의 Measure는 Cross Entroy 방식으로 진행한다고 합니다.


높은 차원의 경우와 관련된 큰 가중치가 있을 때마다 e 점 사이에 인력을 제공합니다.
점들 사이의 거리가 작을 때 w_l(e)가 엄청나게 커질 때 이 텀은 감소하게 된다.
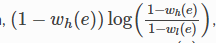
w_h(e)가 작을 때마다 e들의 끝 사이에서 반발력을 제공한다.
여기선 w_l(e)가 작아지게 해서 최소화해야 하기 때문이다.
균형을 이루는 높은 차원 데이터의 토폴로지 표현의 가장자리에 있는 가중치를 매개로 하는 이러한 끌어 오기 및 푸시 프로세스는 원본 데이터의 전체 토폴로지를 상대적으로 정확하게 나타내는 상태로 저 차원 표현을 고정시킵니다.
The UMAP Algorithm (이것만 인식해도 될 듯합니다!)
- 기본적으로 위에서 설명한 대로 퍼지 위상 위상 표현을 구성하는 단계로 구성됩니다.
- 크로스 엔트로피 (cross entropy)에 의해 측정된 것처럼 가능한 한 퍼지 위상 위상 표현을 가깝게 갖도록 저 차원 표현을 간단하게 최적화하는 것입니다.
- 초기 퍼지 위상 구조를 생성할 때 우리는 몇 가지 손쉬운 방법을 취할 수 있습니다.
- 실제로, 퍼지 집합 멤버십의 강도는 사라지기 때문에 사라지기 때문에 각 점의 가장 가까운 이웃에 대해서만 계산하면 됩니다.(그래서 저자가 knn가 비슷하다고 한 것 같습니다)
- 높은 차원의 데이터라고 할지라도 효율적으로 근처를 계산할 필요가 있습니다.
- KNN 같이 Nearest Neighbor에 Descent algorithm을 사용해서 위의 부분을 해결한다고 합니다.
- 남아 있는 계산은 각 포인트에서 local neighbors 다루기 때문에 굉장히 효율적으로 된다고 합니다.
- 초기 퍼지 위상 구조를 생성할 때 우리는 몇 가지 손쉬운 방법을 취할 수 있습니다.
- 저 차원 임베딩을 최적화할 때 우리는 몇 가지 손쉬운 방법을 다시 사용할 수 있습니다.
- use stochastic gradient descent for the optimization process
- Gradient Descent를 더 쉽게 하기 위해서 목적함수를 미분 가능하게 하면 더 이점이 있다고 하는데요.
- 여기서는 1 / 1+ ax^(2b) 형태의 Curve들의 family를 사용했다고 합니다.
- 모든 Edge에서 계산을 하지 않기 위해서 negative sampling trick 사용
- use spectral embedding techniques to initialize the low dimensional representations into a good state
- use stochastic gradient descent for the optimization process
드디어 끝
'관심있는 주제 > Dimension Reduction' 카테고리의 다른 글
| Why You Should Always Use Feature Embeddings With Structured Datasets - 리뷰 (0) | 2021.02.28 |
|---|---|
| 여러가지 구조의 Autoencoders (0) | 2019.06.13 |
| UMAP은 어떻게 작동할까? (Uniform Manifold Approximation and Projection) - 2 (0) | 2019.06.06 |
| UMAP은 어떻게 작동할까? (Uniform Manifold Approximation and Projection) - 1 (0) | 2019.06.05 |