2021.03.13 - [관심있는 주제] - GNN- 1탄 Graph 기본 개념 알아보기
2021.03.13 - [관심있는 주제] - GNN - 2탄 GNN 기본 개념 알아보기
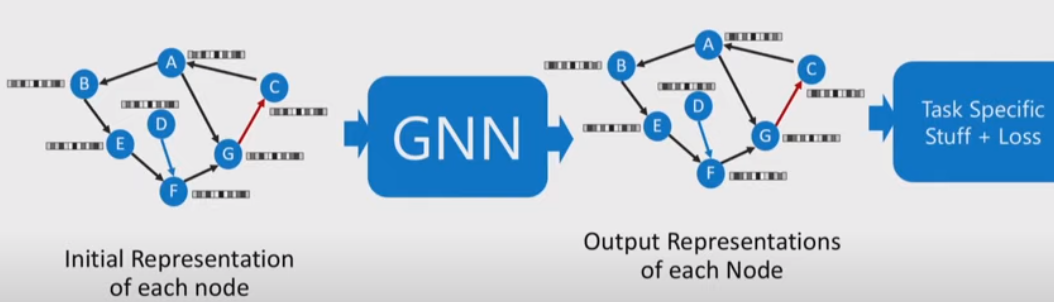
그래프 신경망 (GNN)은 최근 그래프 구조 데이터를 분석하는 능력으로 인해 많은 관심을 받고 있습니다.
최근에 GNN을 쓸 분야가 점점 많아지는 것 같아 공부를 개인적으로 천천히 해보려고 한다.
일단 GNN에 대해서 너무 무지하므로 기본 개념들을 여기저기 찾아서 이해하는 글을 적겠다.
그래프를 이해하기 쉽도록 그래프 이론과 그래프 분석 문제를 다룹니다.
그런 다음 다양한 형태와 원리로 그래프 신경망을 소개한다
또한 GNN이 할 수 있는 작업과 GNN의 일부 응용 프로그램을 다뤄볼 예정이다.
Graph Theory
일단 graph가 먼지 부터 알아보자.
graph에는 2가지 구성요소로 이루어진 데이터 구조다. (vectices와 edges)(꼭짓점과 간선)
objects와 entities 간의 쌍별 관계를 분석하기 위해 수학적 구조로 사용된다.
전형적으로 그래프는 $G=(V,E)$로 정의되며, $V$는 node 집합이고, $E$ 는 edge 집합입니다.

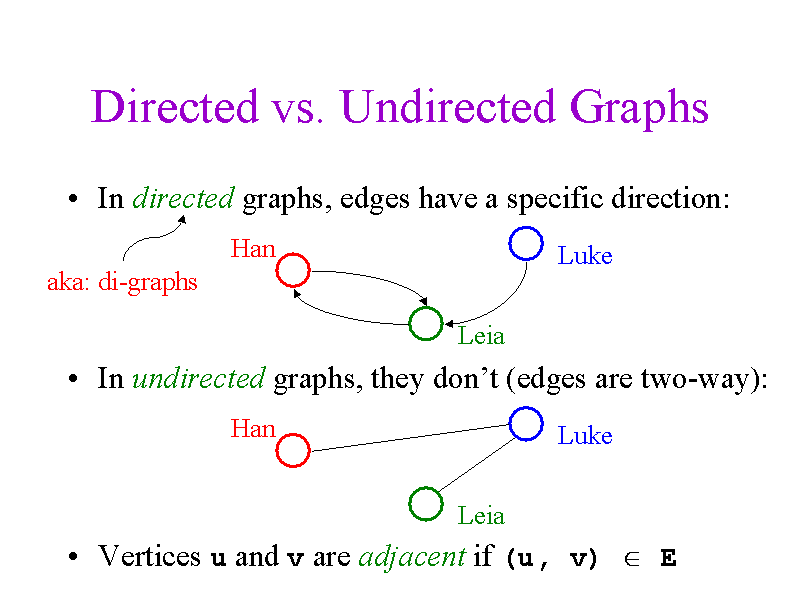
그리고 어떤 참조한 글에 G를 정의한 것을 따르면, 그래프 G는 방향성이 있거나 방향성이 없는 edge로 연결된 node들의 집합이라고 하고, 노드와 에지는 일반적으로 풀고자 하는 문제에 대한 전문가의 지식이나 직관 등에 의해 구성된다고 합니다.(참조)
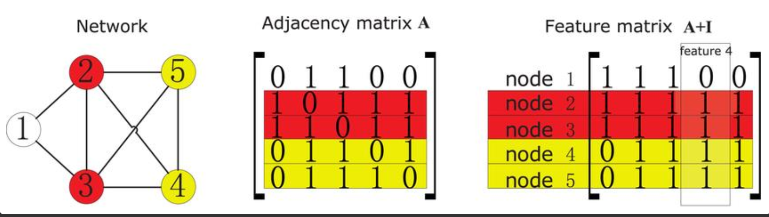
graph는 종종 인접행렬(Adjacency matrix)$A$로 표현됩니다.
만약 그래프가 N개의 node를 가진다면, $A$는 $NxN$ 차원을 가지게 됩니다.
사람들은 때때로 그래프에서 노드들을 설명하기 위하여 feature matrix를 제공한다고 합니다.
각각의 노드들이 피처들의 F 수를 가지면, feature matrix X는 $NxF$ 차원을 가진다고 합니다.


Why Is a Graph Difficult To Analyze?
그렇다면 왜 Graph는 분석하기 어려울까요?
첫번재 이유로 뽑는 것은 그래프에는 euclidean space가 존재하지 않기 때문입니다. euclidean space에 없으면 우리가 친숙한 coordinate systems으로써 표현이 안되기 때문이죠.
이 것은 다른 데이터(이미지, 파동, 타임 시리즈 텍스)보다 graph data의 해석이 더 어렵게 합니다.


두번째 이유로 그래프는 고정된 형태가 아니다.
시각적으로는 두 개의 그래프가 다른 형태인 것을 알 수 있지만, 인접 행렬은 동일한 것을 알 수 있다.
이 경우에 두 그래프를 어떻게 봐야 할 까?(같이 또는 다르게)

마지막 이유로 그래프는 사람이 해석할 수 있도록 시각화하는 것이 어렵다.
위에 같이 간단한 그래프 말고, 복잡한 그래프(node들이 여러 개가 있고 많이 연관됨)에서 말하는 것이다.
차원이 매우 크고 노드가 매우 조밀하면, 사람은 그래프를 이해하는데 어려움을 느끼게 된다.
그러므로 이 테스트에서 기계를 훈련시키는 것은 어렵다.
Why Use Graphs?
그래프를 사용하는 이유는 다음과 같이 요약할 수 있다.
- 관계, 상호작용과 같은 추상적인 개념을 다루기에 적합하다. 그래프를 그려보면 이런 추상적인 개념을 시각화할 때 도움이 된다. 사회적 관계를 분석할 때 기초가 되기도 한다. 그래프는 또한 사회적 맥락에서 관계를 분석하기 위한 자연스러운 기반을 형성합니다.
- 복잡한 문제를 더 간단한 표현으로 단순화하기도 하고 다른 관점으로 표현하여 해결할 수도 있다.(어떻게 보면 관계에 대해서 그 사람 자체보다는 단순히 하나의 노드와 주변 관계만으로 문제를 풀 수 있어 어려운 문제를 단순화 가능하다고 하는 것 같다.)
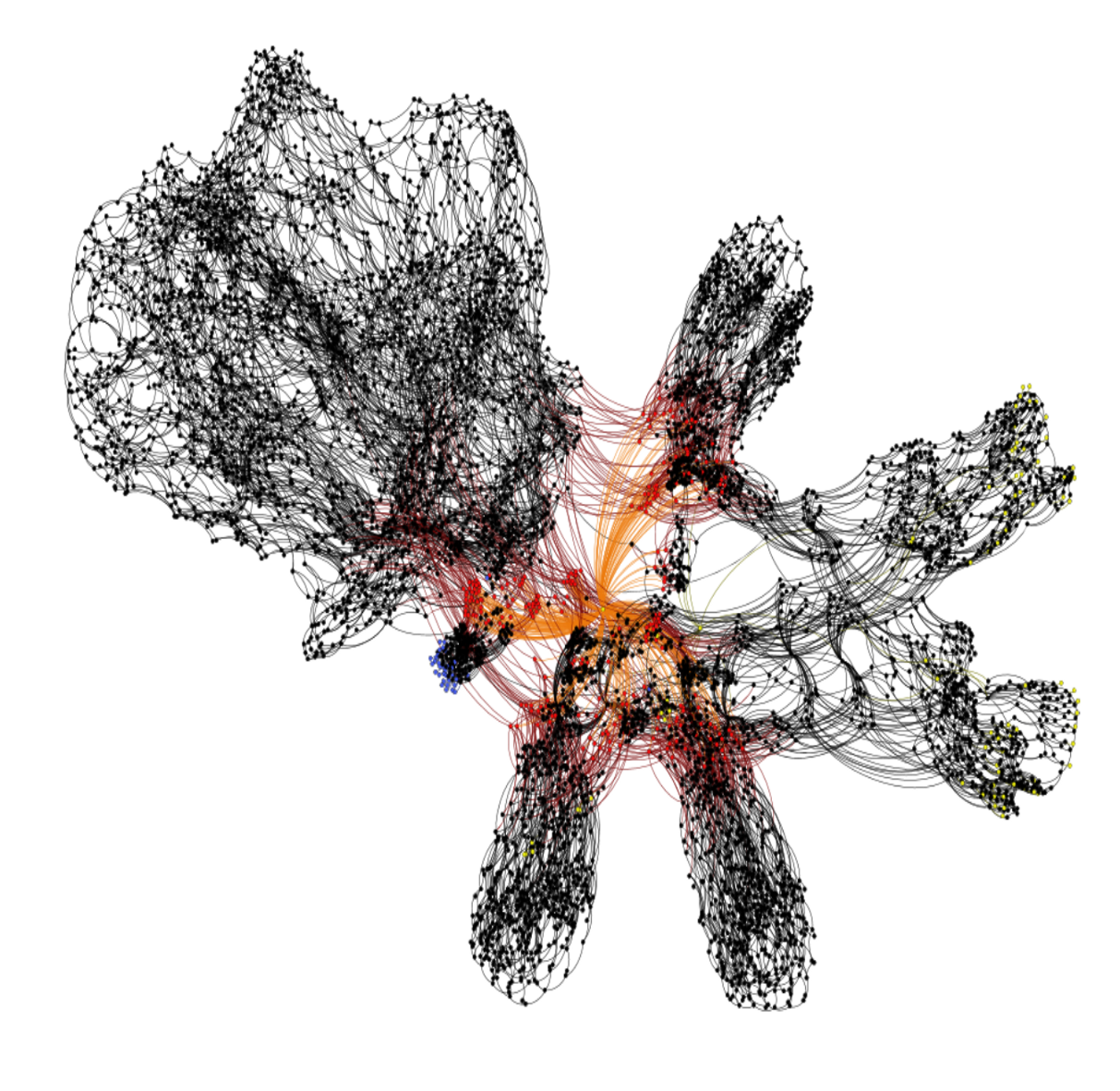
- 소셜 네트워크, 미디어의 영향, 바이러스 확산 등을 연구하고 모델링할 때 사용할 수 있다. 소셜 네트워크 분석은 데이터 과학에서 그래프 이론을 사용하는 가장 잘 알려진 분야일 것이다. 최근 뉴스에서 코로나 19 확산, 이동경로를 나타내고 분석할 때 자주 등장한다. 아래 이미지도 그중 하나이다. (실제로 3번과 같인 이유에서 GNN을 배우고 싶었던 이유가 있다. 복잡한 사람들 사이의 관계를 기존에 내가 알고 있던 지식으로 한계를 느꼈다)

Traditional Graph Analysis Methods
전통적인 방법은 주로 다음과 같은 알고리즘 기반 방법이다.
- searching algorithms, e.g. BFS, DFS
- shortest path algorithms, e.g. Dijkstra’s algorithm, Nearest Neighbour
- spanning-tree algorithms, e.g. Prim’s algorithm
- clustering methods, e.g. Highly Connected Components, k-mean
이런 알고리즘의 한계는 알고리즘을 적용하기 전에 입력 그래프에 대한 사전 지식이 필요하다는 점이다.
그렇기 때문에 그래프 자체를 연구하는 것이 불가능하고, 그래프 레벨에서의 예측이 불가능하다.
여기에서 말하는 ‘그래프 레벨’은 그래프에 속하는 점이나 선에 대한 정보를 다루는 것이 아니라 그래프가 여러 개 있을 때 그래프의 정보를 다루는 것을 말한다.
Non-Euclidean and Graph-structured Data
이미지와 언어를 넘어서는 실제 데이터는 유클리드가 아닌 기본 구조가 되는 경향이 있습니다.
이러한 복잡한 데이터는 일반적으로 과학 및 공학 분야에서 발생하며 이기종 그래프로 직관적으로 모델링할 수 있습니다. 대표적인 예로는 분자 그래프, 컴퓨터 그래픽의 3D 메시, 소셜 네트워크 및 생물학적 네트워크가 있습니다.

다음 글에서는 GNN에 대해서 소개하려고 한다.

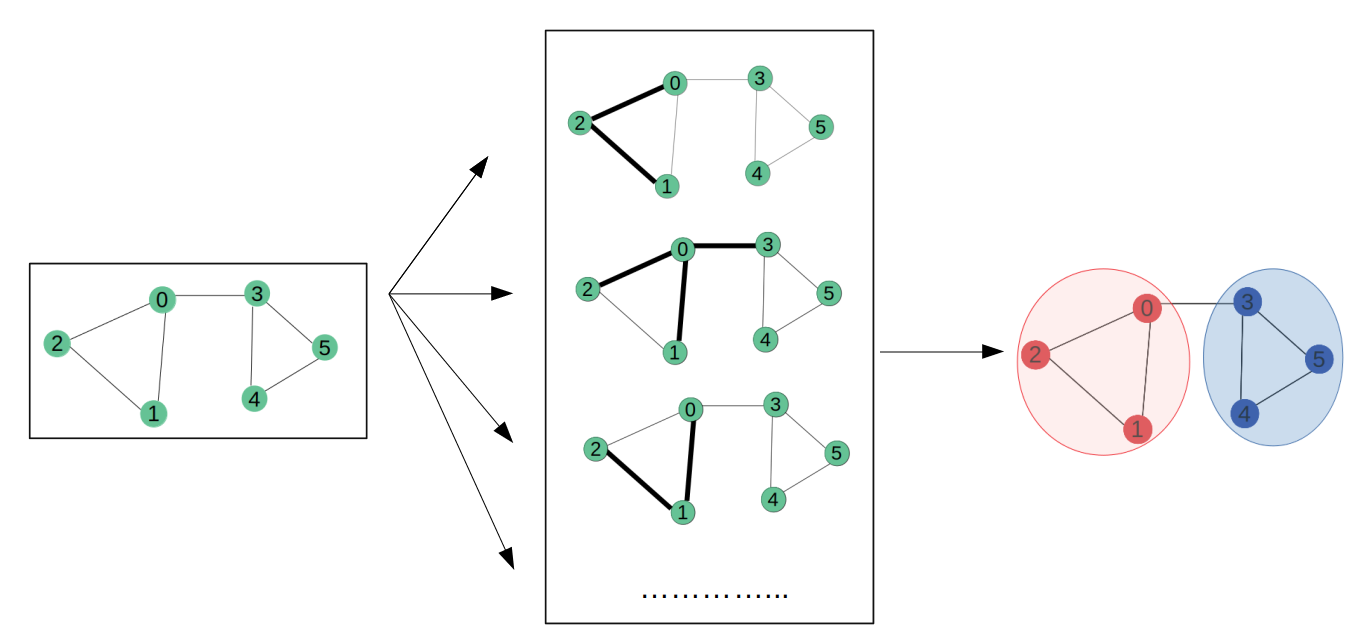
참조 :
www.youtube.com/watch?v=zCEYiCxrL_0
www.ee.iitb.ac.in/~eestudentrg/presentations/Deconvoluting_Graph_Convolutional_Networks.pdf
sailab.diism.unisi.it/gnn/auto_examples/PyTorch_Subgraph/main_subgraph.html
courses.cs.washington.edu/courses/cse326/00wi/handouts/lecture21/sld014.html
www.slideshare.net/JungwonKim10/graph-neural-network
'관심있는 주제 > GNN' 카테고리의 다른 글
| pytorch) Create Your Own GNN DataSets (1) | 2021.04.13 |
|---|---|
| installation) torch_geometric (0) | 2021.04.13 |
| GNN - Application 및 샘플 코드 (0) | 2021.04.13 |
| GNN - survey paper (trend, application) (1) | 2021.04.05 |
| GNN - 2탄 GNN 기본 개념 알아보기 (1) | 2021.03.13 |