2020. 10. 24. 16:11ㆍ관심있는 주제/RL
읽어보니, 현재 내가 찾고자 하는 주제와는 거리가 멀었지만, 추후에 살펴봐야 하는 부분이기에 한번 계속 읽어보기로 함.
아주 간략하게 말하면, 아주 큰 액션 공간을 기존 강화 학습 알고리즘에 맡겨서 학습을 시키는 것은 굉장히 어렵다고 말함. 그래서 저자는 이러한 문제를 해결하기 위해 pro-ation과 knn을 통해 action 선택을 축소한 것 같음.
그래서 본 저자의 논문에서는 state를 통해서 actor가 proto action인 action embedding을 얻게 되고,
action embedding에 knn 방법론을 적용해서 action을 선택하는 2-step 전략을 제안함.

Abstract
많은 수의 개별 행동이 있는 환경에서 추론할 수 있는 능력은 강화 학습을 더 큰 문제에 적용하는 데 필수적이다.
(추천 시스테, 산업 생산
추천 시스템, 산업 플랜트 및 언어 모델은 현재의 방법을 적용하기 어렵거나 심지어는 종종 불가능한 수많은 개별 작업을 포함하는 많은 실제 작업 중 일부에 불과하다.
이러한 작업을 처리하려면 작업 집합에 대한 일반화 기능과 집합 크기에 따른 하위 선형 복잡성이 모두 필요합니다.
저자가 제안한 접근 방식은 작업에 대한 사전 정보를 활용하여 일반화할 수 있는 연속 공간에 포함시킵니다.
또한 근사 최근접 이웃 방법은 시간에 따른 다루기 쉬운 훈련에 필요한 작업 수에 비해 로그 시간 조회 복잡성을 허용합니다.
저자는 강화 학습에 이러한 방법론을 적용하여, 기존에 할 수 없었던 액션 공간이 큰 경우에 적용하였다고 한다.
Introduction
YouTube 및 Amazon과 같은 대형 시스템에 사용되는 추천 시스템은 매초 수억 개의 항목을 추론해야 하며, 대규모 산업 프로세스를 위한 제어 시스템은 매 시간 단계에서 적용할 수 있는 수백만 개의 가능한 조치를 가질 수 있어야 한다.
기존 강화 학습(2016년 이전)에 있던 알고리즘으로는 어려움이 있다고 함.
이 논문에서는 액션의 범위가 큰 경우에도 효율적으로 작동하는 새로운 policy architecture를 제시한다고 함.
저자는 행위에 대한 사전 정보를 활용하여 행위자가 일반화할 수 있는 연속적인 공간에 삽입함으로써 이를 달성함.
이 임베딩은 폴리시의 복잡성을 액션의 수와는 별개로 만드는 것이 가능하게 했다고 함.
저자의 방법론은 space에서 continous action을 만들고, 근사 최근접 이웃 방법론을 통해서 가까운 이상현 액션을 찾는다.
Definitions
크게 특별한 것이 없으니 패스

Problem Description
강화 학습에서 자주 사용되는 policy의 family는 다음과 같다고 함.
1. value-based , 2. actor-based
value-based
가치 기반 정책의 경우 정책 결정은 가치 기능에 직접적으로 좌우됨.
보다 일반적인 예 중 하나는 가치 함수에 비해 탐욕스러운 정책을 적용한 경우가 있음

하지만 value-based 방법론은 smooth function으로 근사하여 사용할 수 있을 때, 액션에 대해서 일반화할 수 있는 속성이 있어야만 함.
만약 $a_{i}$와 $a_{j}$가 비슷하다면, $a_{i}$ 에 대해서 학습하는 것은 $a_{j}$에게 정보를 줄 수 있음.
이를 통해 학습 효율성이 향상될 뿐만 아니라 value based policy가 이전에 볼 수 없었던 작업을 추론하기 위해 작업 기능을 사용할 수 있다.
안타깝게도, 실행 복잡성은 | A | 작업 수가 크게 증가하면이 접근 방식을 다루기 어렵게 만듦
보통 actor-critic 접근에서, policy는 모수화된 actor function으로 정의된다. 실제로 $\pi_{\theta}$는 분류기와 같다. 그러나 actor based 아키텍처는 위의 식 arg max의 모든 작업에 대해 비용이 많이 드는 Q 함수를 평가하는 계산 비용을 피합니다. 그럼에도 불구하고, actor-based 방법론은 value-based 방법론만큼 action space에 대해서 일반화할 수가 없다.
행동 공간과 관련된 하위 선형 복잡성과 행동에 대한 일반화 능력은 우리가 관심 있는 작업을 처리하는 데 필요함.
현재의 접근 방식은 이 두 가지를 모두 제공할 수 없으므로이 논문에 설명된 접근 방식에 동기를 부여했다고 함.
Proposed Approach
저자는 새로운 아키텍처인, Wolpertinger 아키텍처를 제안함.
이 아키텍처는 액션에 대해서 일반화를 유지하면서, 모든 액션을 평가하는 비용을 피할 수 있다고 함.


Action Generation
이 아키텍처는 일단 연속형 공간 안에서 액션을 생성하고, 그 생성된 것을 discrete action으로 다시 매핑해주는 작업을 함.


일단 왼쪽 그림에서 state에서 action space로 정하는 작업을 통해 proto-action을 생성하고, 이 action은 continuous 함
이 continuous 한 $\hat {a}$것을 다시 discrete action으로 매핑을 해주는 g를 거침.
여기서 $g_k$는 knn 방법론(k-nearest-neighbor) 방법론을 사용함. ($L_2$ 방법론을 통해 가장 가까운 행동을 정함)
위에 설명된 가치 함수 파생 정책의 arg max와 복잡성이 동일하지만, 각 평가 단계는 전체 value function 평가가 아니라 L2 거리임.
위에 아키텍처에서 보는 것처럼 actor를 통해 action embedding 값을 추출하고, knn으로 실제 액션으로 매핑을 해주는 것을 알 수 있다.
Action Refinement
action representation이 얼마나 잘 구조화되어 있는지에 따라, 낮은 Q- 값을 가진 행동은 대부분의 행동이 높은 Q- 값을 갖는 공간의 일부에서도 때때로 $\hat{a}$에 가장 가깝게 위치할 수 있다.
추가적으로, 어떤 행동은 행동 임베딩 공간에서 서로 가까이 있을 수 있지만, 어떤 상태에서는 이웃에 비해 장기적인 가치가 특히 낮기 때문에 구별되어야 함.
이 두 경우 모두 이전에 생성된 일련의 작업에서 $\hat {a}$에 가장 가까운 요소를 선택하는 것은 이상적이지 않습니다.
이상치 행동을 뽑는 것을 회피하기 위해서 Q-Value를 기반으로 가장 높은 것을 선택함으로써 액션의 선택을 재정제함.

Training with Policy Gradient
중간에 KNN을 쓰는 것은 신기했지만, 어떻게 애를 학습시키는가 궁금했는데, 저자도 이 부분에 완전 미분이 가능하지도 않다고 말함. 그래도 우리는 policy를 잘 학습했다고 말함.
(중간에 더 썼는데, 따른 것도 해야 하니.. 나머지는 대충 씀!)
Experiments
다들, 액션 스페이스가 큰 경우를 의미한다고 함.
Discretized Continuous Environments
Cart-Pole(Real Simulator)

Multi-Step Plan Environment
Puddle World

Recommender Environment
Recommendation Task

Conclusion
이 논문에서는 대규모 개별 작업 공간에서 효율적으로 학습하고 행동할 수 있는 새로운 정책 아키텍처를 소개했음.
DDPG를 사용하여, 아키텍처를 학습하는 방법을 설명하고 수천에서 백만 개의 개별 작업 범위로 일련의 작업에서 우수한 성능을 보여줬다고 함.
이 유형의 아키텍처는 정책에 작업 수에 비해 하위 선형 복잡성으로 작업 집합을 일반화할 수 있는 기능을 제공함.
전체 작업 집합의 하위 집합만 고려하는 것이 많은 작업에서 어떻게 충분하고 상당한 속도 향상을 제공하는지 보여줌.. 또한 가장 가까운 이웃 조회에 대한 대략적인 접근 방식을 달성할 수 있지만 종종 성능에 약간만 영향을 미칠 수 있음을 보여줌.
다음 논문의 향후 작업은 훈련 중에 동작 표현을 학습할 수 있게 하여 임베딩 공간에 잘못 배치된 동작이 공간의 더 적절한 부분으로 이동할 수 있도록 하겠다고 함.
또한 이러한 방법을 보다 광범위한 실제 제어 문제에 적용하는 방법을 조사할 계획입니다.
큰 액션 공간에서 어떠한 선택을 강화 학습한테 설계할지도 생각해보면, 어려운 문제인 것 같다.
기존에 나와있는 코드들은 간단한 행동들이나 하나의 행동을 결정하는 것이 대부분인데, 이러한 논문을 통해서 강화 학습을 다중 액션에 적용 시 어려운 점도 듣고, 막연히 추천에 적용할 수 있다고는 알고는 있었지만, 이 논문을 보니, 실제로 추천에 강화 학습을 잘 사용하는 것이 많이 어려울 것 같다고 판단하게 되었다...
핵심 아이디어 Code 일부
실제로 코드를 보면 다음과 같음.
ddpg_select_action에서 proto_action을 생성하고,
search_point에서 proto_action을 기반으로 actions을 선택함.
아래 search_point를 보면, flann이라는 knn 패키지를 써서 값을 찾는 것을 확인할 수 있었음.
def select_action(self, s_t, decay_epsilon=True):
proto_action = self.ddpg_select_action(s_t, decay_epsilon=decay_epsilon)
# print("Proto action: {}, proto action.shape: {}".format(proto_action, proto_action.shape))
# print(proto_action)
actions = self.action_space.search_point(proto_action, self.k_nearest_neighbors)[0]
# print("len(actions): {}".format(len(actions)))
states = np.tile(s_t, [len(actions), 1])
a = [to_tensor(states), to_tensor(actions)]
# print("states: {}, actions: {}".format(a[0].size(), a[1].size()))
actions_evaluation = self.critic([to_tensor(states), to_tensor(actions)])
# print("actions_evaluation: {}, actions_evaluation.size(): {}".format(actions_evaluation, actions_evaluation.size()))
actions_evaluation_np = actions_evaluation.detach().numpy()
max_index = np.argmax(actions_evaluation_np)
self.a_t = actions[max_index]
return self.a_t def search_point(self, point, k):
p_in = self.import_point(point).reshape(1, -1).astype('float64')
# print("p_in: {}, p_in.shape: {}, p_in.dtype: {}".format(p_in, p_in.shape, p_in.dtype))
search_res, _ = self._flann.nn_index(p_in, k)
knns = self.__space[search_res]
p_out = []
for p in knns:
p_out.append(self.export_point(p))
if k == 1:
p_out = [p_out]
return np.array(p_out)
다른 의견이지만, 읽다 보니 같은 state에서 multipe action을 하는 것을 Slate MDP라고 한다고 함.
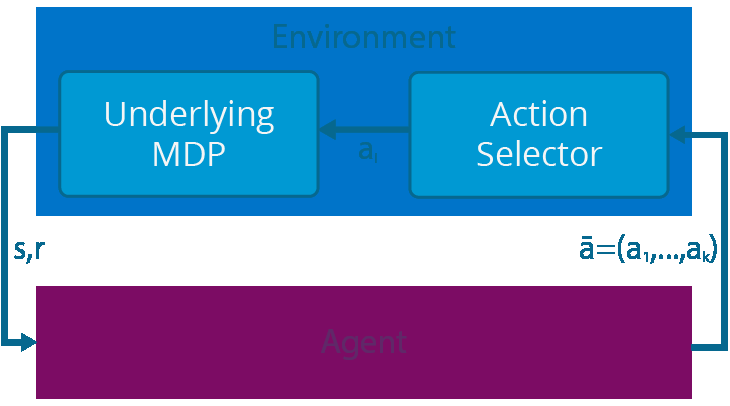
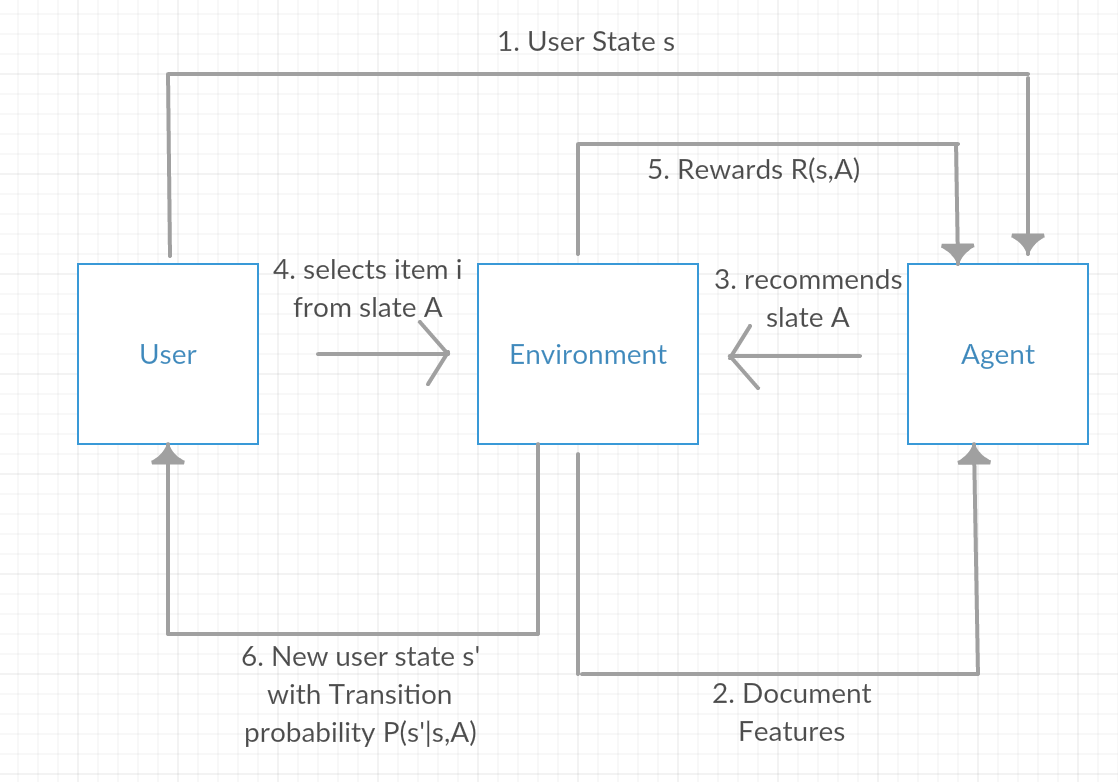
A Slate-MDP is an MDP with a combinatorial action space consisting of slates (tuples) of primitive actions of which one is executed in an underlying MDP. The agent does not control the choice of this executed action and the action might not even be from the slate, e.g., for recommendation systems for which all recommendations can be ignored.
Reference
paper:
github:
github.com/nikhil3456/Deep-Reinforcement-Learning-in-Large-Discrete-Action-Spaces
'관심있는 주제 > RL' 카테고리의 다른 글
| [Review] Distral: Robust Multitask Reinforcement Learning 논문 (0) | 2020.11.04 |
|---|---|
| [Survey / RL] Action Masking 관련 자료 (0) | 2020.10.24 |
| RL multiple action space일 경우 단순 고민... (0) | 2020.10.24 |
| RL Environment Open Source (0) | 2020.09.29 |
| Model-based RL 알아보기 (0) | 2020.09.26 |