강화 학습은 우리의 행동에 대한 보상을 극대화합니다.
아래 수식처럼, 보상들은 정책(Policy)과 시스템 역학(model)에 의존한다.
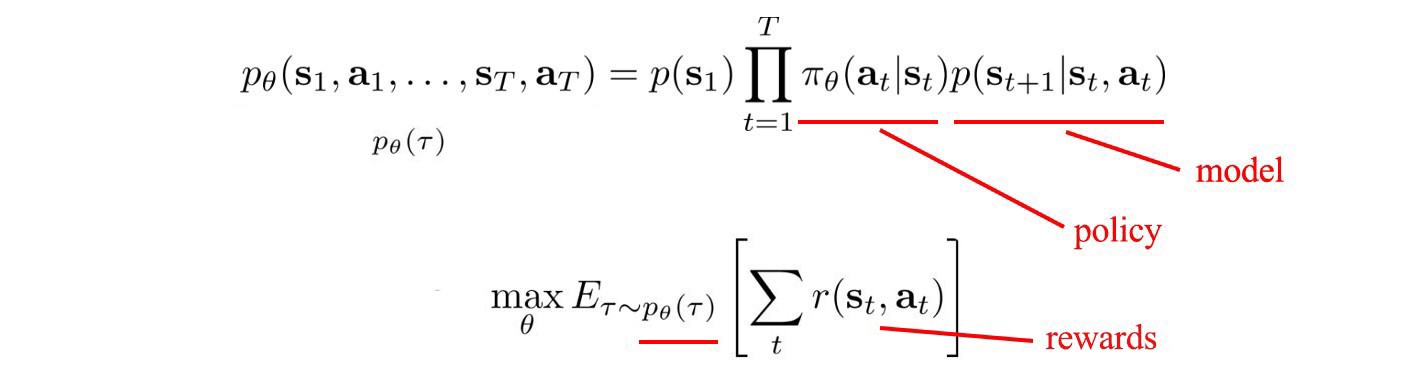
model-free RL에서는, 모델을 무시한다.
보상을 평가하기 위해서 샘플링과 시뮬레이션에 의존한다. 그래서 우리는 시스템의 내부적인 작업을 알 필요가 없다.
model-based RL에서는 만약 우리가 우리 스스로 cost function을 정의할 수 있다면, 직접적으로 model을 사용하여 최적의 action을 계산할 수 있다.
RL은 크게 Model-free와 Model-based로 나눌 수 있다.
이 미디엄 글에서는 model을 어떻게 확립하고, 그것을 최선의 의사결정에 활용할 것인가에 대해 토론할 것이다.

Terms
Control Theory는 Model based RL와 강하게 영향성을 가진다.
그러므로 먼저 몇 가지 조건을 살펴보자.
강화 학습에서 우리는 행동을 결정하는 최적의 정책을 찾는다.
제어 이론에서 우리는 제어기를 최적화한다는 의미이다.

Control은 강화학습에서 Action의 또 다른 용어일 뿐이다. Action은 종종 states($s$ or $x$)에서 $a$ 또는 $u$로 쓰인
다. Controller는 model을 사용하여 states와 controls의 순차적으로 표현된 최적의 trajectory에서 control를 결정한다.
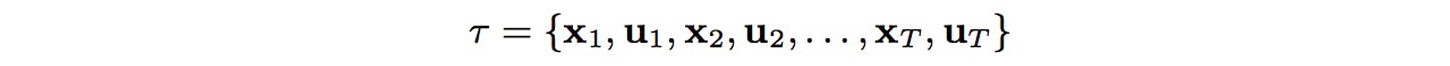
model-based RL에서는 maximum reward를 하는 대신에 최소한의 cost를 위해서 trajectory를 최적화한다.
Model-free RL vs Model-based RL
전에 언급된 것 같이, Model-free RL은 model을 무시한다. 그리고 내부 작업에 대해서 신경을 덜 쓴다.
우리는 보상을 추정하기 위해서 샘플링으로 돌아간다.

보상을 최대화하는 정책을 찾기 위해서 Policy Gradient, Value Learning 또는 다른 Model-free RL를 사용한다.

반대로, Model-based RL은 Model에 초점을 맞춘다.

cost function과 함께, 최소의 비용을 가지는 최적화된 trajectory를 찾는다.
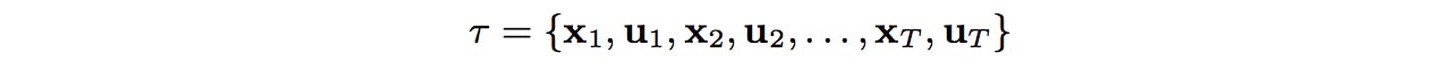

Known models
GO와 같은 많은 게임에서 게임의 규칙은 모델(model)이다.

다른 케이스에서, 물리학 법칙이 있다. 때때로, 우리는 그것을 모델링하고 그것을 위한 시뮬레이터를 만드는 방법을 알고 있다.
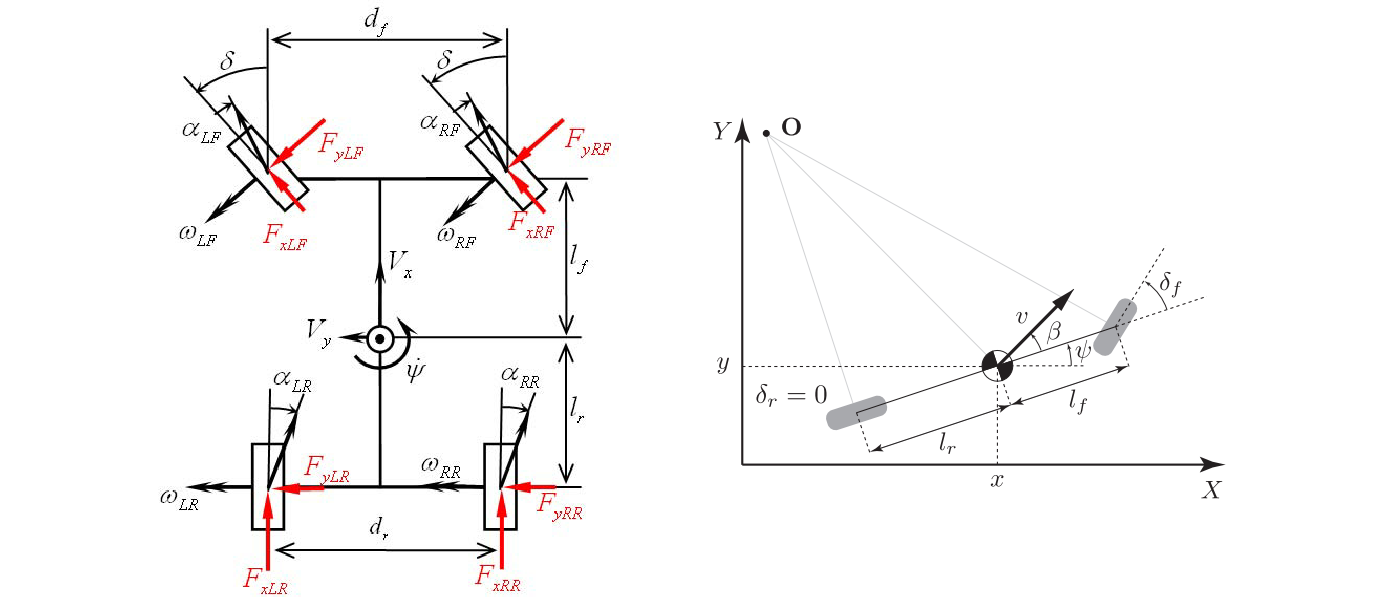
수학적으로, Model은 next state를 예측한다.

우리는 룰 또는 등식으로 Model을 정의한다. 또는 우리는 Gaussian Process(GP)나 Gaussian Mixture Model(GMM) 또는 Deep Network를 사용하는 모델링한다. 이
러한 모델들을 적합시키기 위하여, 샘플 trajectories를 모으고, 지도 학습에서 모델들을 훈련하기 위해서 controller를 사용한다.
Motivation
Model-based RL은 샘플 효율성을 가진다는 강한 장점을 가진다.
많은 Model들은 로컬 근접에서 선형적으로 동작한다. 그들을 학습하기 위해서 매우 적은 샘플이 필요로 한다.
모델과 cost function을 안다고 할 때, 우리는 sampling 없이 최적의 controls를 구상할 수 있다.
아래에서 보이는 것처럼 On-policy Policy Gradient 방법들은 10M training iteration을 수반한다. 반면에 Model Based RL은 100번의 training iteration안에서 가능하다.
간단한 작업을 하는 물리적 로봇을 학습하기 위해서, Model-Based 방법은 20분 만에 가능하지만, Policy Graident 방법은 몇 주가 걸린다. 그러나 이러한 장점은 물리적 시뮬레이션들이 컴퓨터 시뮬레이션으로 대체할 때 사라진다.
왜냐하면, Model based 방법들에서 경로(trajectory) 최적화는 훨씬 더 복잡하기 때문에 컴퓨터 시뮬레이션이 충분히 정확한다면 Model free RL이 더 유리할 것이다.
또한 계산을 간단하게 하기 위해서, Model based 방법론들은 더 많은 가정들과 근사치를 가지고 있다. 그러므로 훈련된 모델을 더 작은 작업으로 제한하게 된다.
즉, 실제 물리적 시뮬레이션이 있는 환경에서는 Model Based RL이 좋지만, 이것을 컴퓨터 시뮬레이션으로 하게 되면, 많은 가정과 근사치를 사용하기 때문에 좋지 않은 성능을 가지고 있고, 훈련을 할지라도 기존 task 범위보다 더 작은 범위에서 밖에 사용할 수 없는 것이다.

Learn the model
Model-based RL에서는, 모델이 알려져 있거나, 학습할 수 있다. 뒤에 나올 경우에서,
우리는 base policy를 운영(랜덤 또는 이미 학습된 policy)하고, trajectory를 관측한다.
그때, 우리는 샘플링된 데이터를 사용하여 모델에 적합한다.

위의 step 2에서, 표본 추출된 경로(sampled trajectory)로 부터 최소 제곱 오차(least square error)를 최소화하는 model을 학습하기 위해서 지도 학습(supervised learning) 사용한다.
3 step에서는 iLQR과 같은 어떤 궤적 최적화 방법을 사용한다. 그때, 모델을 이용하여 최적 궤적을 계산하고, 우리가 목표 위치로부터 얼마나 멀리 떨어져 있는지, 얼마나 많은 노력을 기울였는지 측정하는 비용 함수를 계산한다.
(iLQR은 또 다른 글을 참고해야 할 듯하다. medium.com/@jonathan_hui/rl-lqr-ilqr-linear-quadratic-regulator-a5de5104c750)
즉 만약 Model based RL을 하기 위해서는 model를 만들어야 하는데, 그때 샘플링된 데이터를 사용하여 지도 학습을 한다. 학습을 통해서 샘플링에서 만들어진 경로와 실제 경로 간의 차이가 적은 것을 model 만들어야 한다는 것이다.
Learn the model iteratively
그러나, 표류하기 쉽다는 문제가 있다. 작은 오차들은 trajectory가 흘러감에 따라서 빠르게 누적된다.
이 탐색 공간은 너무 커서 어떤 기본 정책도 완전히 커버할 수가 없다.
model이 아직 배우지 못했던 지역에 도착할지도 모른다.
이러한 영역에 대한 적절한 model이 없으면 최적의 제어장치를 계획할 수 없다.

이를 해결하기 위해서, 처음부터 model을 학습하는 대신, 우리는 길을 따라 이동하면서 model을 계속 샘플링하고 맞추게 된다.

step 2와 step4를 반복한다. 그리고 샘플들을 모으는 과정을 계속하고, 검색 공간(search space) 주변 model을 적합한다.
즉, 한 번에 모든 trajectory를 학습할 수 없으니, 조금씩 앞으로 이동하면서 model을 위해서 데이터를 샘플링하고 맞추는 작업을 진행
MPC (Model Predictive Control)
그럼에도 불구하고, 이전 방법은 다시 model을 적합시키기 전에 모든 계획된 행동을 실행한다.
하지만 이 방법은, 이미 모인 데이터로 인해서 기존 경로랑은 멀리 떨어지게 될지도 모른다.

MPC에서 전체 궤적(whole trajectory)을 최적화하지만 첫 번째 action만 취한다.
관측하고 그리고 다시 계획한다.
재계획은 current state를 다시 관찰한 후 시정조치를 취할 수 있는 기회를 준다.
확률적 모델의 경우, 이것은 특히 도움이 된다.

이것만 봐도, 단순 강화학습 학습하기 전에, model 만드는 과정도 산 넘어 산이다.
끊임없이 계획을 변경함으로써, 우리는 model의 문제에 덜 취약하다. 따라서, MPC는 우리가 훨씬 덜 정확한 모델을 가질 수 있게 해 준다.
이 개념에 따라 모델이 어떻게 훈련되는지에 대한 비디오가 있다.
drive.google.com/file/d/1pASnlyCEaW8B0ocGfKI_5eg1GrnSvV1d/view
stacking.mp4
drive.google.com
Backpropagate to policy
controller에 의해서 생성된 iLQR과 같은 경로 최적화 방법론을 사용하는 controls은 model과 cost function을 사용하여 계산된다.

그러나, deep network 또는 GP를 사용하여, 직접적으로 policy $\phi$를 model를 사용한다.
예를 들어, 주어진 action에서 next state를 예측하기 위해서 우리는 model을 사용한다.
그때, 우리는 다음 action을 결정하기 위해서, policy를 사용한다. 그리고 비용을 계산하기 위해서 action과 state를 사용한다. 마침내 우리는 policy를 훈련하기 위해서 비용을 역전파한다.
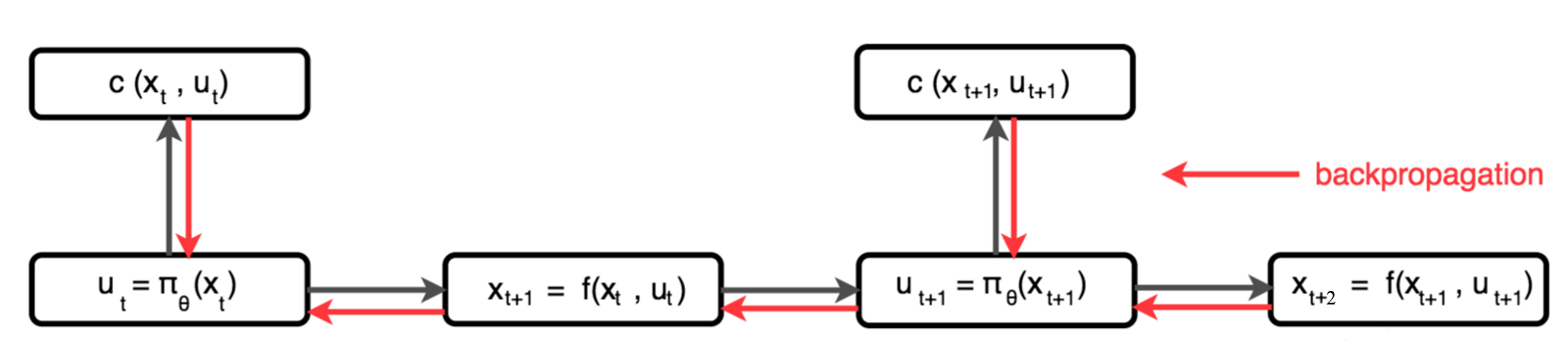

dynamic model을 만들고, 함수를 통하여 정책을 역전파로 학습한다.
PILCO
역전파를 통하여, 직접적으로 정책을 학습하는 PILCO 알고리즘이다.

그러나, trajectory에서 consecutive states는 매우 상관성이 있다.
상관관계가 있는 값을 갖는 백 프로 파게이 션 함수는 종종 소멸하거나 폭발하는 그러데이션으로 이어진다.
그래서 그 약속은 제한되어 있다.

Global Model
시스템 역학을 나타내기 위해 어떤 종류의 모델을 사용할 수 있는가?
한 가지 가능성은 가우스 과정이다. 직관은 간단한다. 만약 2개의 인풋들이 유사하다면, 그 아웃풋도 유사하다는 것이다.
두 개의 데이터 포인트에서, 만약 한 개가 알려진 훈련 데이터와 가깝다면, 다음 예측도 명확하다는 것이다.

각각 f(x1)=150과 f(x2)=200으로 관측된 두 데이터 점을 x1과 x2로 표본 추출했다. x1 <x2>에 대한 f(x)의 가능한 값을 결정할 수 있는가? 위의 그림은 하나의 표준 편차 내에서 f(x)의 가능한 값을 보여준다.
표시된 것처럼 x1과 x2 사이의 중간점은 값에 대한 불확실성이 가장 높아야 한다. f¹and f² 와 같은 데이터 포인트의 출력은 다음과 같은 형태로 가우스 분포로 모델링할 수 있다.


175의 f의 평균이다. K는 covariance matrix이다. 각각의 요소(i, j)는 input $x_i , x_j$사이에서 유사성을 측정한다.
For details on how to calculate K, please refer to here.
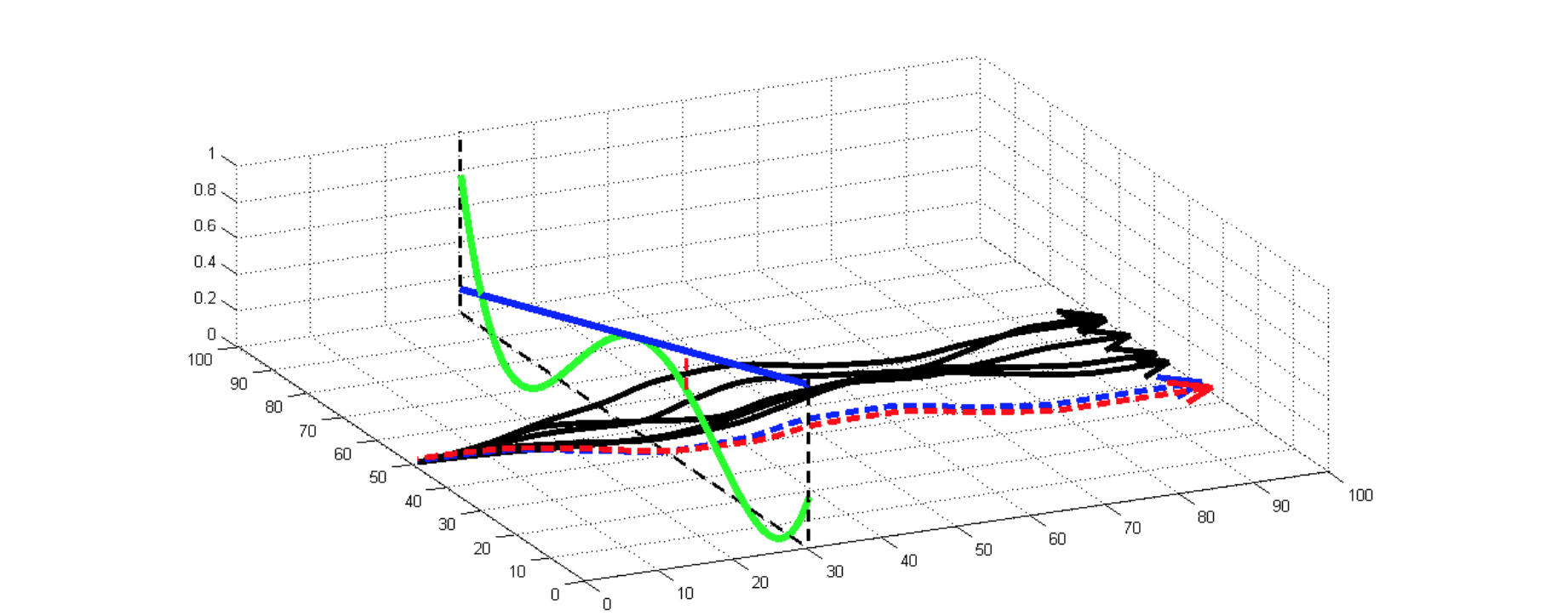
아래의 오른쪽 그림은 5개의 데이터 포인트의 출력을 샘플링한다. 그래프는 가우스 공정을 사용하여 예측을 표시한다. 파란색 선은 평균을 나타내고 음영 영역은 한 표준 편차(SD) 내의 값을 나타낸다. 따라서 입력 x=5의 경우 한 SD 내의 예측은 -1.1에서 -0.4 사이, 평균은 -0.7이다.


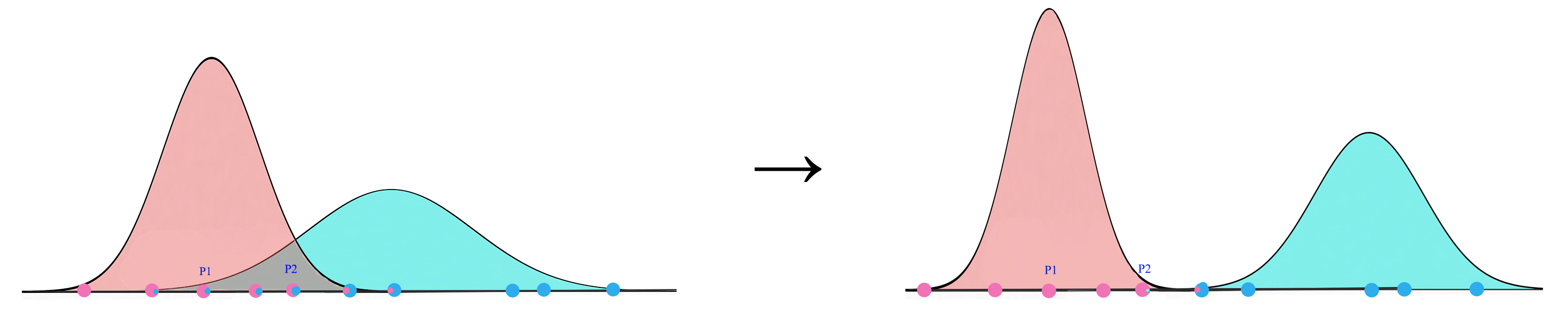
또 다른 가능성은 GMM이다. Gaussian Mixture Model은 K 개의 Gaussian 분포의 혼합이다.
우리는 model이 가장 가능성이 높은 결과를 가지고 있다고 가정하고 우리는 각 가능성을 다음과 같이 가중치 부여한다.


이러한 K개의 Gaussian distribution 인식하기 위해서, 우리는 k clusters(mode)에서 샘플 데이터를 군집화하기 위해서 EM(Expectation-Maximization)을 사용한다. 각각의 값은 평균과 분산을 표현한다.
Deep network
Global model
이전에 우리는 글로벌 모델로 역학을 모델링(model)했다. 역동성이 복잡하다면 딥 네트워크처럼 좀 더 표현력 있는 모델(model)이 필요하다. 하지만 그것을 훈련시키려면 많은 샘플이 필요하다.
만약 우리가 아직 제대로 훈련되지 않은 공간에 착륙한다면, model은 잘못되어 훈련의 진행을 파괴하는 나쁜 행동으로 이어질 수 있다.
Local Model
필요할 때 지역적으로 model을 개발할 때 on-demand 접근을 채택할 수 있다.
local model은 선형 역학을 가진 가우스 분포다.

선형 역할을 가지는 파라미터는 계산된다.

다음으로 우리가 어떻게 훈련하고 컨트롤러를 사용하여 조치를 취하는지를 볼 것이다.
Controller

우리는 로봇의 제어기 p를 작동시키고 궤적(trajectory)을 관찰한다.
수집된 샘플로 우리는 샘플을 사용하여 파생 모델을 추정함으로써 지역적으로 모델(model)을 맞출 수 있다.
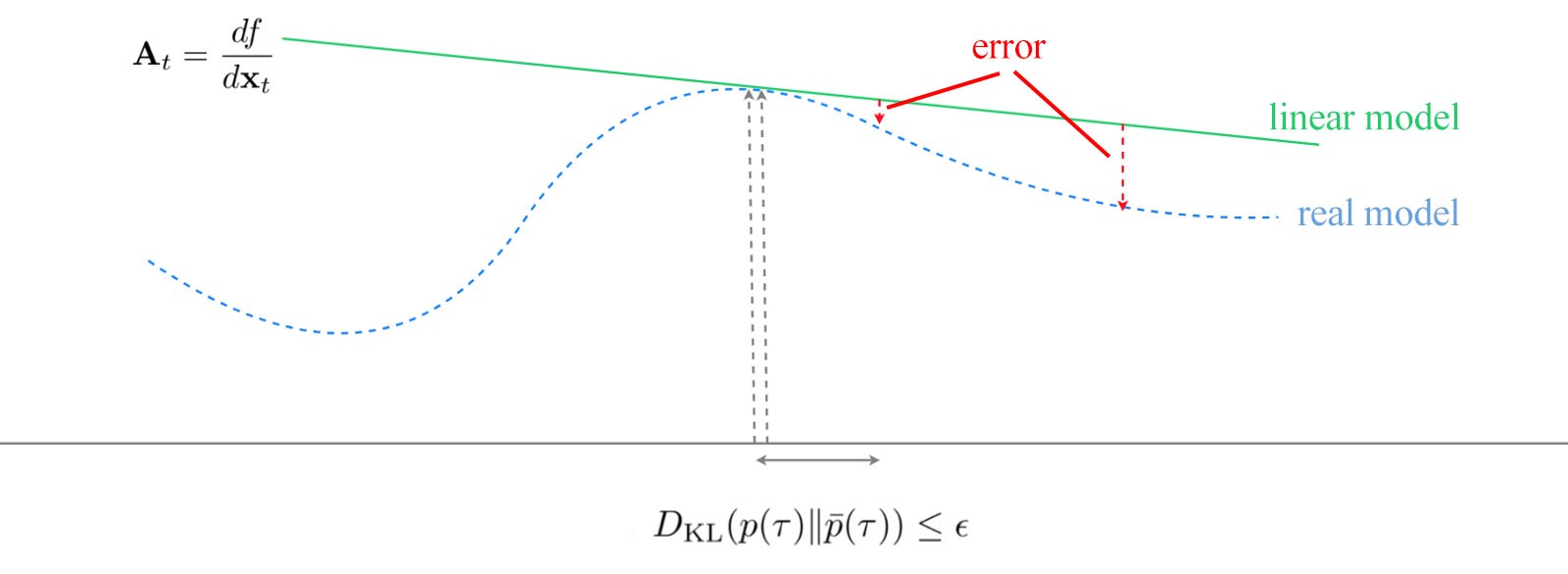
그러나, 잠재적인 에러는 local model로 개발된 궤적(trajectory)으로부터 멀리 떨어졌을 때, 오차가 증가한다.
따라서 우리는 궤도 최적화가 신뢰 영역 내에서 이루어지도록 제약조건을 추가한다. 요컨대, 최적화 결과를 신뢰할 수 없는 이 지역 밖에서는 조치를 취하지 않을 것이다.
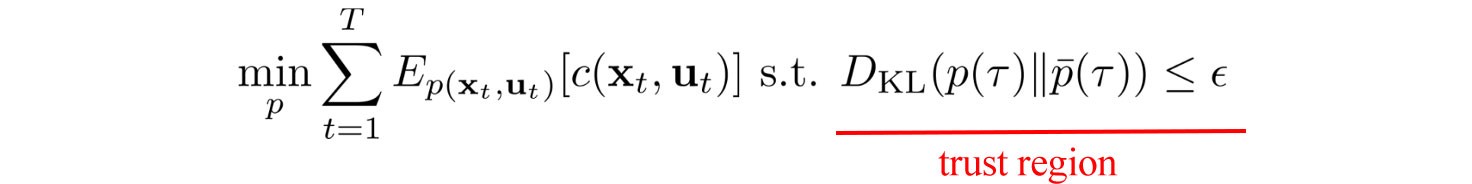
trust region는 새로운 컨트롤러와 오래된 컨트롤러 사이에서 차이를 측정하는 KL로 결정된다.
만약 궤적(trajectory)이 샘플링된 것과 너무 차이가 난다면, 공격적으로 될 수 있고, 계산된 값이 실제 값과 너무 멀어질 수 있다.

그래서 controller는 어떤 걸 사용해야 하는 걸까?
만약 controller이 훈련 중에 같은 state에 대해 같은 action을 반복해서, 탐구한다면 너무 지루할 것이다.
반복 샘플은 model을 더 좋게 만들기 위한 새로운 정보를 제공하지 않는다.
따라서 우리는 선형 가우스 컨트롤러를 사용하면 동작을 더 잘 탐색한다.(가우시안 분포 결과 행동이 있는 선형 동적)
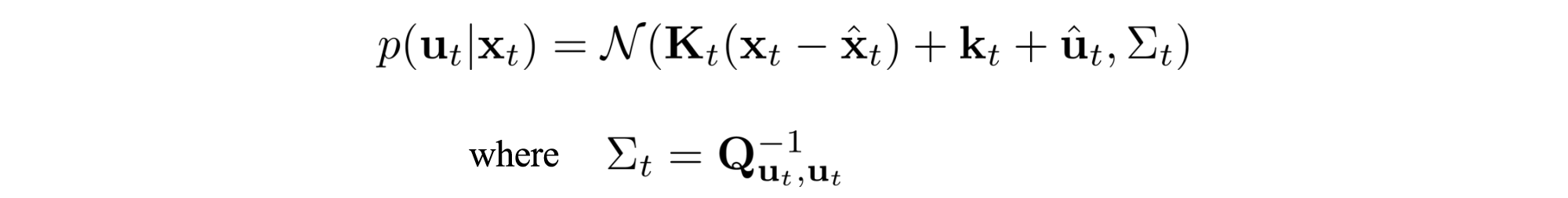

$\sum$ 은 const Q가 작을 때 크다.
그래서 우리는 예상 비용이 낮을 경우 탐험을 중단하도록 허용한다. 그렇다면 컨트롤러 변경이 신뢰 영역 내에 있는 경우 비용을 최소화하는 데 있어 새로운 컨트롤러를 어떻게 찾을 수 있는가?
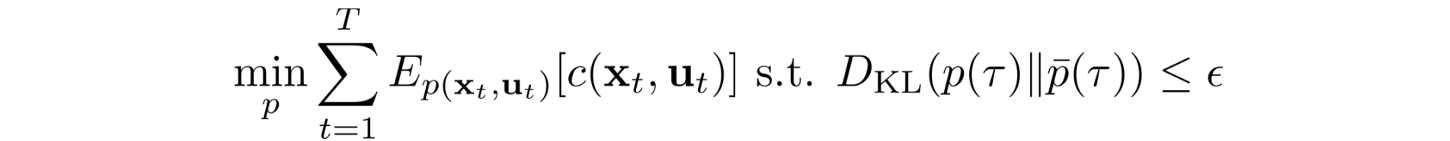
이것을 해결하기 위해서, 우리는 새로운 controller와 오래된 controller를 사이의 KL divergence 특성들 중 일부를 확인할 필요가 있다. 이것은 약간의 수학이 수반되겠지만, 약간의 수학이 수반되겠지만, 그것을 빨리 훑어보는 것이 따라오기에는 쉬울 것이다.
KL-divergence
KL Divergence를 이용해서 old controller와 new controller 간의 궤적(trajectory) 차이를 최소화하도록 한다.


(Note: both trajectories have the same initial and final state.)
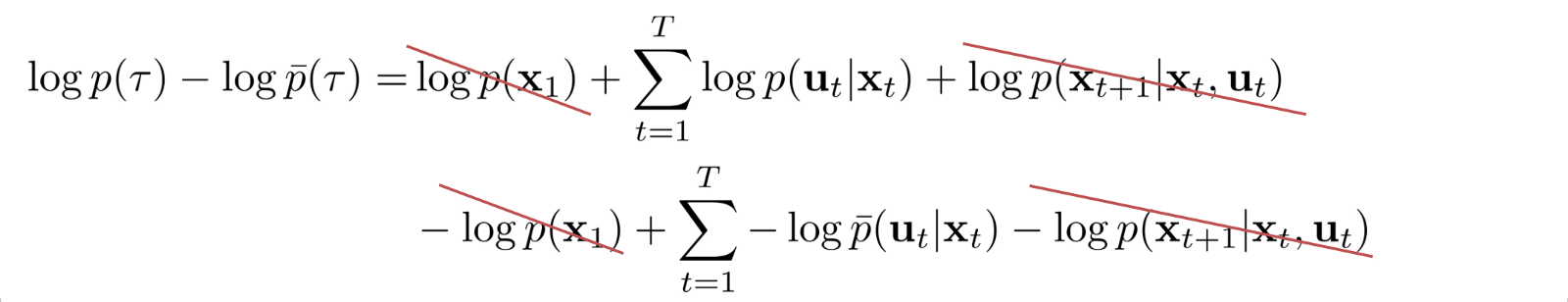
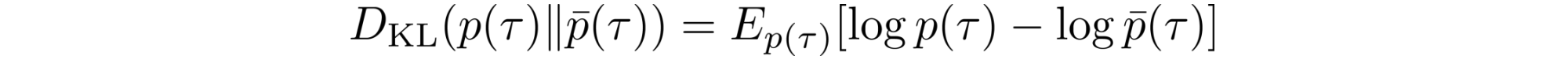
이 등식을 활용해서 KL Divergence가 아래 log로 사용한 것을 알 수 있다.
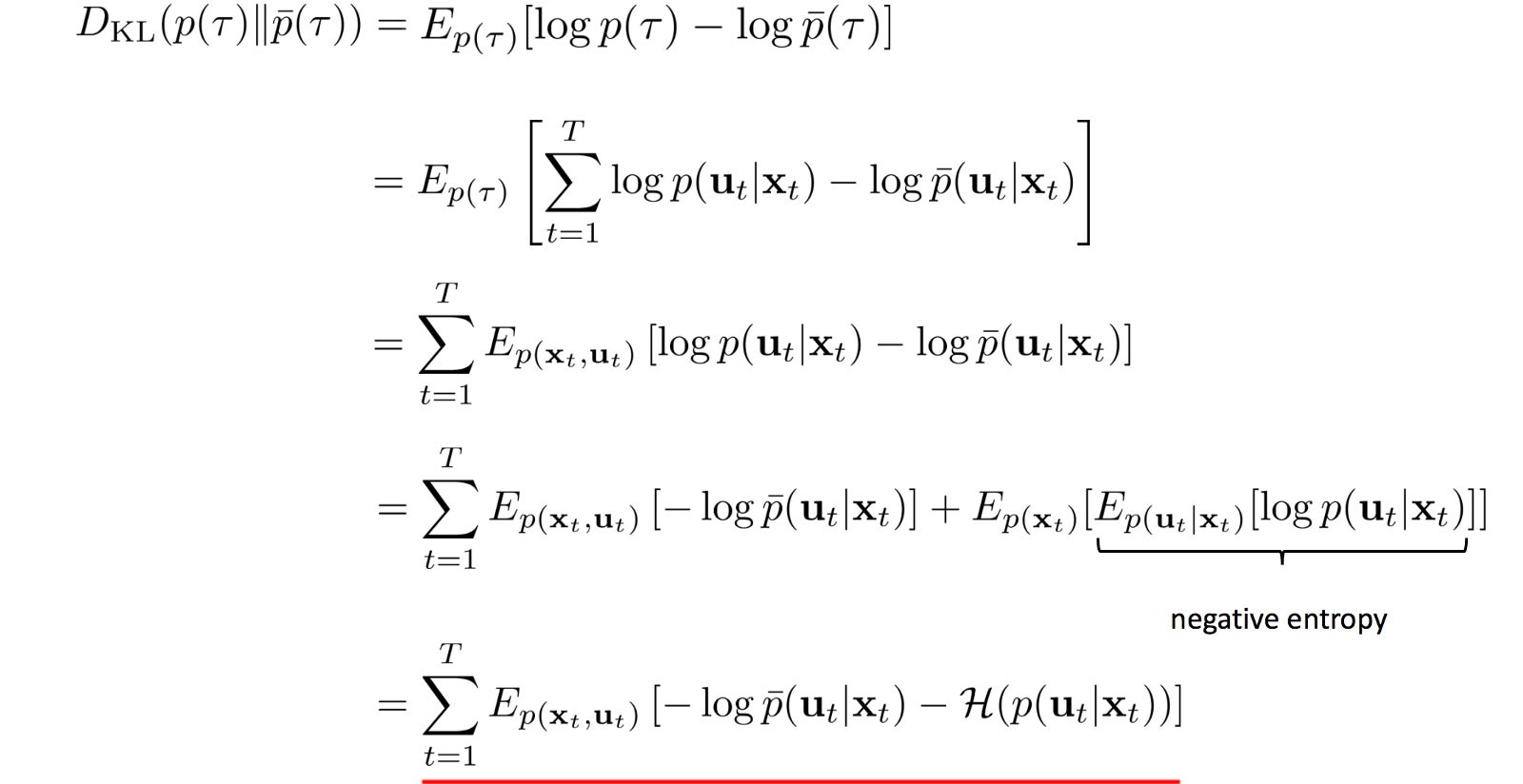
Dual Gradient Descent
다음으로, 제약과 함께 최적화 방법을 할 필요가 있다.

DGD는 선택사항이다. 여기서는 간략하게 설명하고 디테일한 것을 원한다면 DGD를 참고해라.
먼저 Lagrangian과 다음과 같이 정의되는 Lagrange 이중 함수 g를 찾아야 합니다.

우리의 objective의 최적 x는 아래와 같은 방법으로 찾아진다.

직관적으로, 우리는 $\lambda$로 임의의 값들에서 시작하여, 최적화 방법론을 사용하여 𝓛의 최적 값을 찾는다.
우리의 맥락에서 이것은 LQR과 같은 궤도 최적화 방법이 될 것입니다. 여기서 증명 없이 g (i.e. 𝓛(x*, λ)) 는 우리의 목적의 하한이다. 따라서 g를 따라 이동하여 목적 함수에 점점 더 가까워진다.
기울기 하강법을 사용하여 $\lambda$를 g가 증가하는 방향으로 이동하는 2단계와 3단계다.
그런 다음 새로운 $\lambda$로 새로운 하한 g를 계산한다. 반복을 계속하면서, g의 최댓값이 목적함수의 회소값이 닿는 $\lambda$를 찾을 수 있다.
Model-based RL with local model
목적은 다음과 같다.

STEP 1을 최적화하기 위해서 LQR을 사용
LQR은 매우 복잡하지만이 맥락에서 LQR이 궤적 최적화 방법이라는 것을 알면 됩니다. 더 많은 것을 원한다면 나중에 LQR을 읽을 수 있습니다.
우리의 목적함수의 Lagrangian은 다음과 같다.
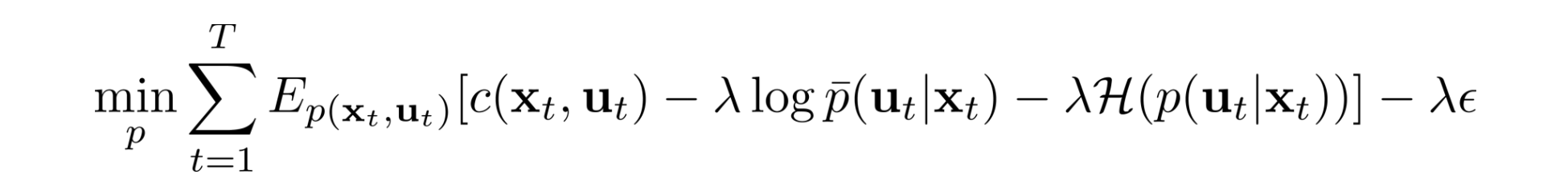
목적을 λ로 나누고 새로운 대리 비용 함수를 생성한다.



선형 가우시안 컨트롤러를 사용하면
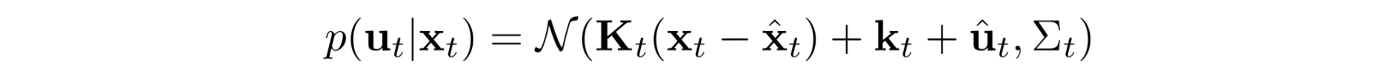
아래 목적을 최소화하기 위해서 LQR을 적용한다.
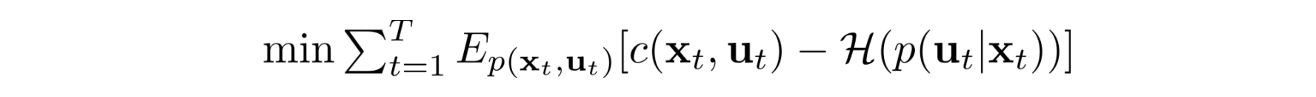
이것은 우리의 목표와 거의 동일해 보이지만 위의 방정식은 원래 비용 함수 c를 사용합니다. 따라서 목표를 해결하기 위해 동일한 절차를 따르지만 c 대신 대리 비용 함수를 사용할 수 있습니다.
Optimize trajectory with a local model

Planning
시뮬레이션한 결과물들을 생성하기 위해서 planning을 사용한다. 그리고 결과물들 value function이나 더 나은 policy로 적합하기 위하여 사용한다.

learning과 planning의 차이는 환경에서 생성하였는지, model에 의한 시뮬레이터 된 경험으로부터 생성되었는지에 따라 달라진다.
value function을 적합하기 위해서 실제 경험을 사용한다. transiotion model를 구축하고, model로부터 경험들을 추출한다. 이는 샘플 데이터가 재사용되고 V에 대해 더 정확한 값을 생성하기 때문에 샘플 효율성을 향상합니다.
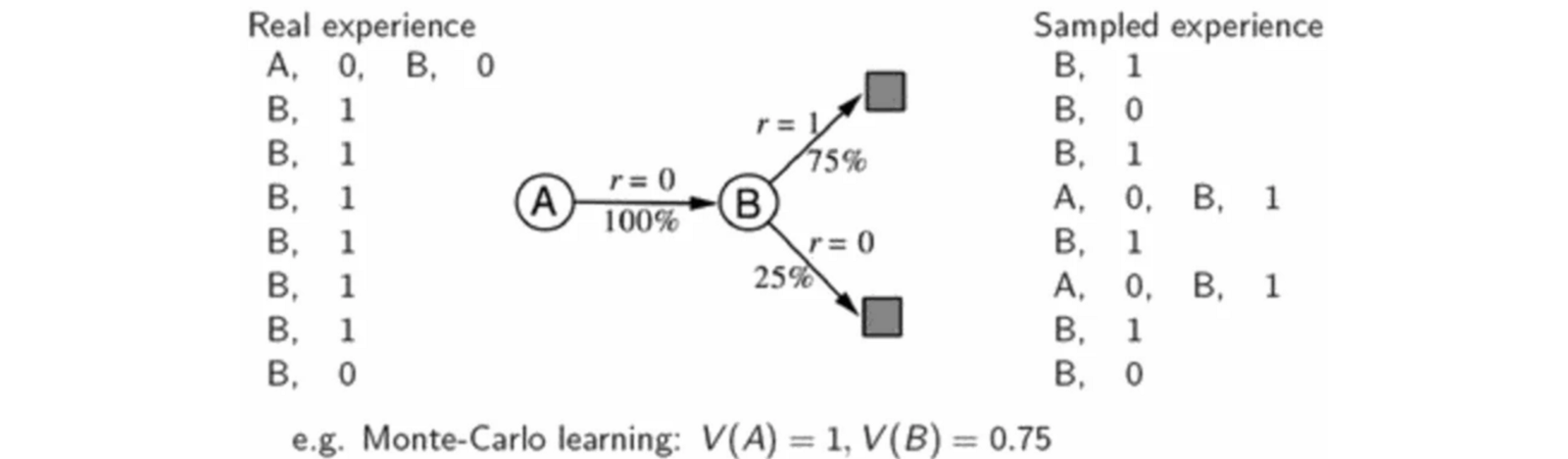
Dyna-Q Algorithm
다음은 샘플링된 데이터와 모델을 사용하여 Q- 값에 맞는 Dyna-Q 알고리즘이다.

Q function으로 행동을 결정하고, Model을 이용해서 next state와 r을 얻는다.
그러나 큰 샘플에서 평균을 내면 줄일 수 있습니다. 물리적 시뮬레이션이 필요한 경우 비용이 많이 듭니다. 그러나 우리는 모델이 있고, 우리는 모델에서 필요한 데이터를 생성할 수 있습니다.
Overfit
model-based 방법에서, 계산 복잡도 때문에, 훈련 샘플을 상대적으로 적은 양을 사용한다. 게다가, 시스템 역학을 modeling 하기 위하여, deep network를 사용한다.
그럼에도 불구하고, 모델의 수용성을 작게 할 필요가 있다. 그렇지 않으면, 이것은 과적합되기 때문이다.
과적합된 모델은 결국 나쁜 결정을 하게 한다.
그러나 이 간단한 model은 최대 보상이 제한되기 된다. 예를 들어, 아래의 Cheetah task에서, Model-based 방법은 500 이하로 총보상을 도달할 수 없다. 더 얻기 위해서는 더 많은 훈련 데이터로 복잡한 모델을 만들 필요가 있다.
더 실현 가능한 설루션은 간단한 모델을 훈련시키기 위하여 Model-based 방법을 사용하는 것이다.
그때, model-free learner를 초기화하기 위하여 이러한 모델을 사용하고 모델이 없는 교육을 사용하여 예상되는 보상을 더욱 향상한다.

Model-based RL with ensembles
독립적으로 훈련된 모델이 동일한 실수를 하지 못하게 한다는 아이디어를 기반으로 앙상블 방법을 사용하는 것이다.
그리고 많은 약한 러너들은 좋은 의사결정을 만들기 위하여 결합된다.
그래서 하나의 model을 훈련하는 대신, 많은 다른 모델들을 훈련하게 위해서 다른 시드들을 사용한다.

Planning에서, 주어진 행동들에서, 각각의 모델로부터 상태 전이(state transition)를 결정하고, 보상을 찾을 수 있다.
행동 시퀀스의 보상은 모든 가능한 모델들을 사용하여 평균 보상들과 같다.
Distillation
과신(overconfidence)은 항상 죽인다. 우리의 데이터를 라벨링 할 때, 확실한 답을 얻을 수 있다.
그러나 현실에서 이것은 덜 명확하다. 앙상블 방법에서 하나의 문제는 k models에서 k 배로 계산 복잡성이 있다.
성능을 일치시킬 계획이지만, 추론 중에는 하나의 모델만 사용한다. 여전히 앙상블 모델을 훈련시키고 앙상 발의 예측을 소프트 라벨(soft label)로 사용한다.
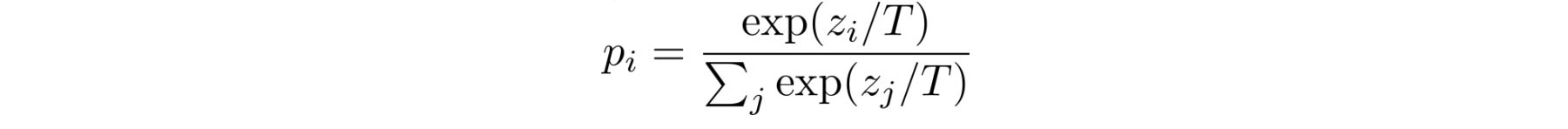
T는 tunable parameter Temperature이다. $z_i$는 ensemble의 logit 결과물이다.
soft label 대신에 값을 맞추려는 의도로 다른 모델을 훈련시킵니다. 직관적으로 앙상블이 예측할 수 있는 것에 대한 새로운 모델을 만든다.
이 전략은 다중 목적을 위해서 단순 정책을 생성하기 위해서 적용된다.
예를 들어, 아래의 각각 아타리 게임에서 정책을 훈련시킬 수 있다.
이 정책들이 훈련될 때, 이 정책들을 예측할 수 있는 것들을 매칭 하기 위해서 지도 학습을 사용한다.
이 목적함수는 간단히 통합 정책의 가중화된 log probability이다. 가중치들은 각각 다른 정책들로부터 이끌어진다.

Thoughts
value function 또는 정책을 적합하기 전에, 우리는 내부 작업이 더 잘 이해하기 위한 model 개발을 필요로 한다.
작동 방식을 알면 물리적 시뮬레이션이 비쌀 때 핵심적인 판매 포인트 인 필요한 샘플 수가 줄어듭니다.
여기에서는 모델 학습의 기본에 대해 설명합니다. 그러나 나는 그것이 그렇게 간단하기를 바랍니다.
model learning은 매우 어렵고, 다른 작업에 대해 잘 일반화되지 않을 수 있습니다.
raw image를 직접적으로 학습하는 것은 정보가 엉켜져 있으면 어렵다.
So if you want a way to check if an RL algorithm is model-based or model-free, ask yourself this question: after learning, can the agent make predictions about what the next state and reward will be before it takes each action? If it can, then it’s a model-based RL algorithm. if it cannot, it’s a model-free algorithm.
www.quora.com/What-is-the-difference-between-model-based-and-model-free-reinforcement-learning
What is the difference between model-based and model-free reinforcement learning?
Answer (1 of 5): To answer this question, lets revisit the components of an MDP, the most typical decision making framework for RL. An MDP is typically defined by a 4-tuple (S, A, R, T) where S is the state/observation space of an environment A is the set
www.quora.com
RL — Model-based Reinforcement Learning
medium.com/@jonathan_hui/rl-model-based-reinforcement-learning-3c2b6f0aa323
'관심있는 주제 > RL' 카테고리의 다른 글
| RL multiple action space일 경우 단순 고민... (0) | 2020.10.24 |
|---|---|
| RL Environment Open Source (0) | 2020.09.29 |
| [RL] RL이 다른 ML가 다른 점을 보여주는 참고 자료들 (0) | 2020.09.06 |
| [RL] Great Reward Function 만들 때 참고 (0) | 2020.09.06 |
| [RL] Create Environment 만들 때 참고 (2) | 2020.09.06 |