Why Do GANs Need So Much Noise? - 리뷰

GAN에 왜 그렇게 많은 노이즈가 필요한가?라는 주제로 미디엄 글이 있어서, GAN 쪽에서 이런 원론적인 것에 대해 관심이 많기 때문에 읽어보려고 한다.

GAN (Generative Adversarial Networks)은 오래된 "실제" 샘플로써 제공하여 새로운 "가짜"샘플을 생성하는 도구이다.
이 샘플들은 이 샘플은 실제로 무엇이든 될 수 있습니다: 손으로 그린 숫자, 얼굴 , 손으로 그린 숫자, 얼굴 사진, 표현주의 그림
이것을 하기 위해서, GANs는 original dataset 하에서 기존 분포를 학습한다. 학습을 통하여, 생성자는 분포를 근사하고 반면에 판별자는 무엇이 잘 못되었는지를 말해준다. 그리고 이 2개가 교호하면서, arms race를 통해서 향상한다.
분포로부터 랜덤 샘플들을 뽑아내기 위해서, 생성자는 인풋으로서 랜덤 노이즈를 받습니다.
그러나 왜 GAN에 무작위 입력이 필요한지 궁금한 적이 있습니까?
이것에 대한 흔한 답으로는 "매번 같은 것을 생성하지 않습니다." 그리고 이 말은 사실이다.
그러나 이 답은 약간 미묘하다.

---

Random Sampling

GAN을 계속 진행하기 전에 우회하여 정규 분포에서 샘플링을 고려해 보자.
당신은  절대 numpy 문서를 읽지 않을 것이고 np.random.normal이 존재하는 것을 잘 모를 것이다. 대신에 파이썬에서 이것을 하고 싶지만 numpy 문서를 읽지 않고 np.random.normal ()이 존재하는지 모른다고 가정해보자. 
대신, 해야 할 일은 random.random ()이며, 간격 (0, 1)에서 균일하게 값을 생성합니다.

Figure 1: A histogram of 100k samples drown from our input, uniform distribution (blue) and our target, normal distribution (orange).

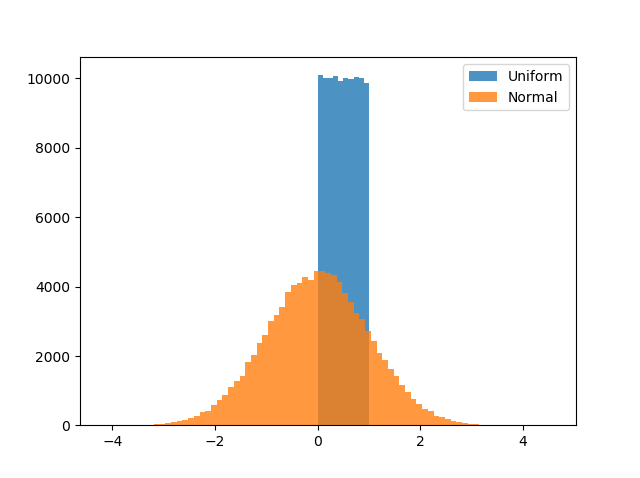
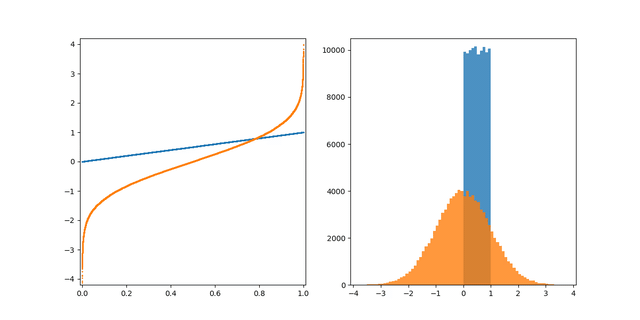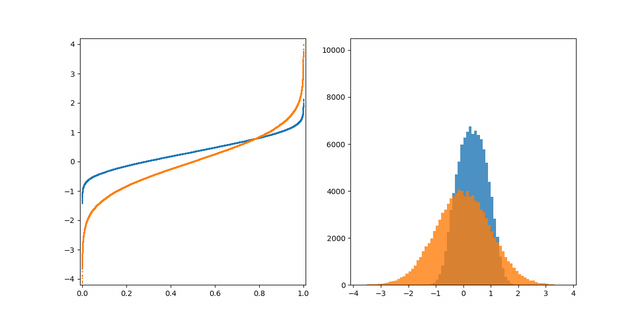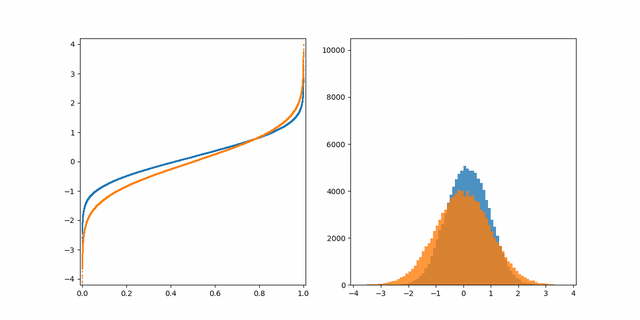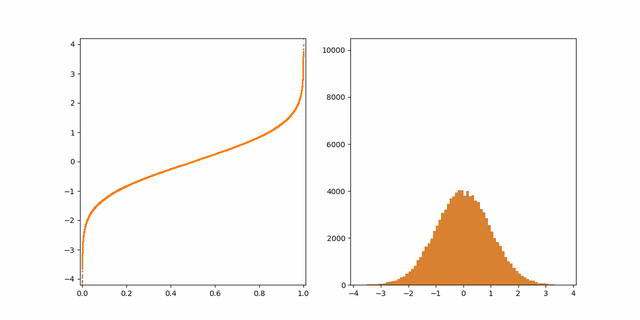
간략히 말해서, 우리는 파란색 분포에서 오렌지 분포로 변형하고 싶다. 다행스럽게도, 이것을 하기 위한 함수는 있다.
(the inverse cumulative distribution function) 이것은 quantile function으로 불린다.
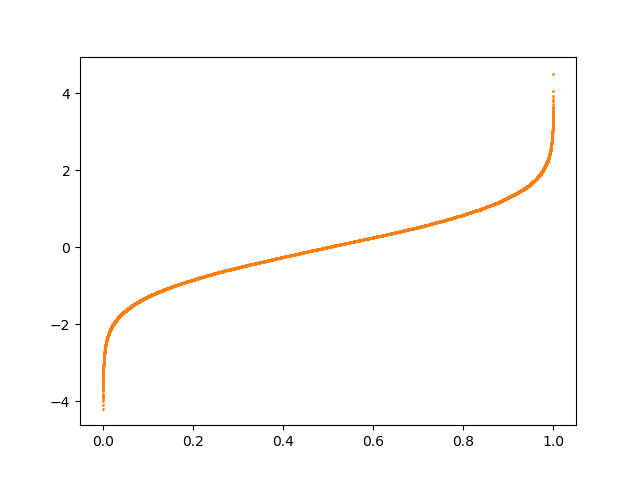
the (non-inverted) cumulative distribution function or CDF는 그림 2에서 설명된다.
CDF는 특정 분포 x에 대해 해당 분포에서 추출된 임의의 값이 x보다 작거나 같을 확률을 설명합니다.

그림 2. The CDF of the standard normal distribution.

예를 들어, 그림 2에 X=0에서 Y =0.5 이것은 0 아래로 분포의 50%가 있다는 것을 의미한다.
CDF의 유용한 특징은 output의 범위가 0에서 1이라는 것이다. 이것은 정확히 random.random () 함수에서 우리가 사용할 수 있는 입력 값이다! 만약 CDT를 뒤집는다면 qunatile function을 얻을 수 있다.

그림3. The quantile function of the standard normal distribution. 

이 함수는 quantile (x(0~1))과 normal distribution에서 상응대는 값과의 정확한 관계를 줄 수 있다. 
인풋 공간의 각각의 점은 아웃풋 공간의 unique point에 상응하게 된다.
> 각각의 인풋이 결국 중복되지 않고, 유니크하게 아웃풋 공간에 맵핑이 된다는 의미?!

Figure 4: An animation illustrating the uniform distribution (blue) being mapped to the normal distribution (orange) using the quantile function.

 

---

What does this have to do with GANs?

위 시나리오에서 우리는 처리할 때 Quantile 함수를 가졌지 만, 입력 공간에서 출력 공간으로의 맵핑을 배워야 한다면 어떨까요?
이것이 바로 GAN이 해결하고자 하는 문제입니다.
이전 글에서, data emergency에 있고 Quantile 기능을 사용할 수 없는 경우 GAN을 사용하여 정규 분포에서 표본을 추출하는 방법을 설명했습니다. 이러한 관점에서, GAN을 무작위 샘플링을 위한 도구가 아니라 일부 k- 차원 잠재 (입력) 공간을 p- 차원 샘플 (출력) 공간에 매핑하는 함수로 생각하면 훨씬 도움이 된다. 

이러한 관점에서, 이 관점에서는 Quantile 함수와 마찬가지로 임의성이 없다.

맵을 염두에 두고 입력으로 0과 1 사이의 1D 랜덤 샘플만으로 2D 정규 분포에서 랜덤 샘플을 추출하는 방법을 고려해본다. 

Figure 5: A 2D normal distribution (orange) and a 1D uniform distribution (blue), each with 100k samples.

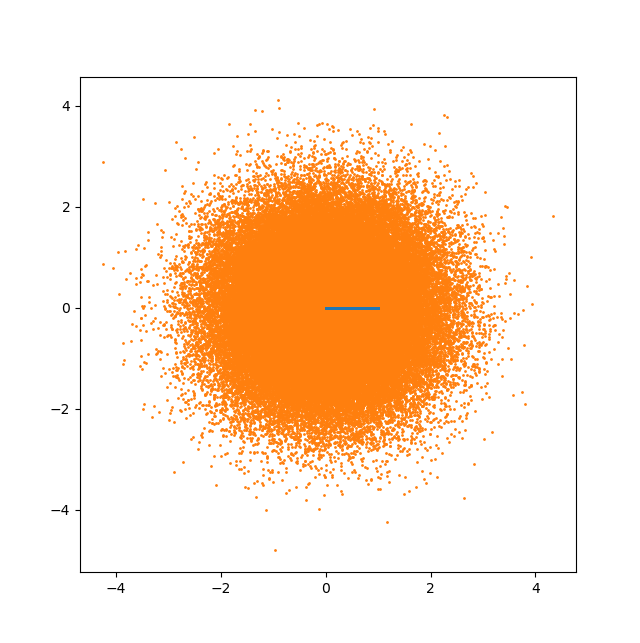
파란색 선의 100k 샘플을 주황색 얼룩의 100k 샘플에 어떻게 매핑합니까?
좋은 방법은 없습니다. 물론, 우리는 Peano 곡선을 사용할 수 있지만, 입력 공간에서 포인트를 서로 가깝게 하는 유용한 특성을 잃어버리고 출력 공간에서 포인트를 서로 가깝게 하고 그 반대도 마찬가지입니다.

이것은 GAN의 latent dimensionality가 sample space의 차원보다 동등하고 많아야 하는 이유이다.
즉, 이 함수는 인풋에서 아웃풋으로 맵핑하기 위한 충분한 자유도를 가져야 한다.

만약에 1차원 인풋으로 다차원 분포를 배우는 것을 시각화해봤다고 한다. 
결과는 당신을 놀라게 하지 않을 것이지만, 보는 것은 흥미로울 것이다.

---

2D Gaussian

1D (0~1)에서 2D normal distribution으로 맵핑한 것이다. 

Figure 6: A GAN with a latent dimension of 1 trying to learn the 2D Gaussian distribution. Grey points are samples drawn from the true distribution, red points are generated samples. Each frame is one training step.

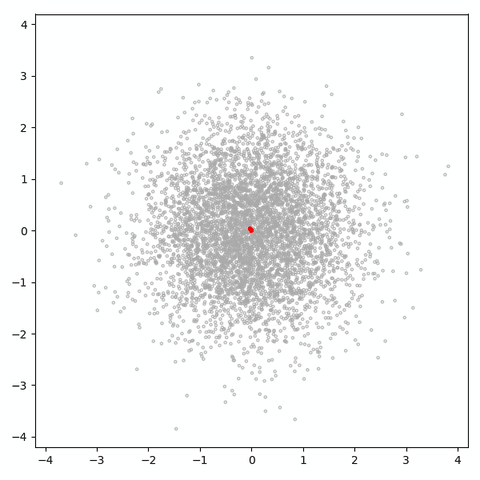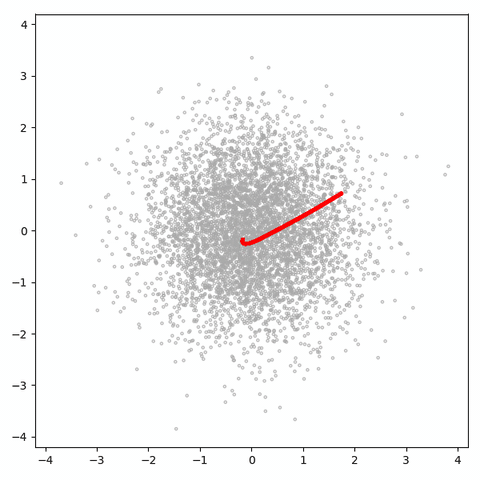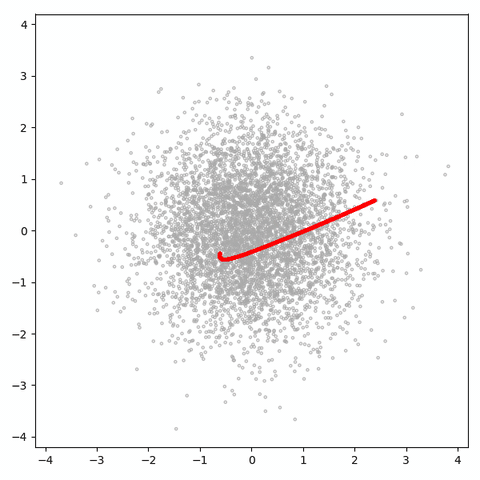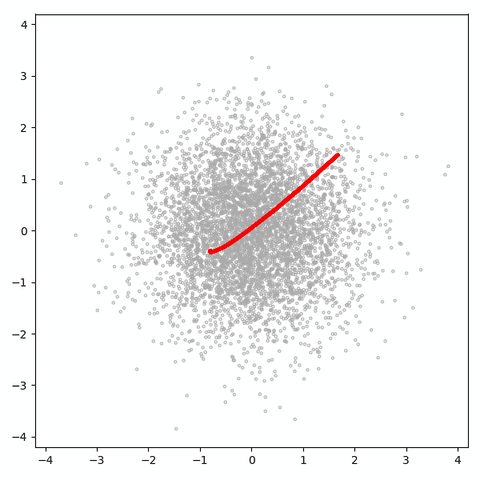
이걸 보면 알 수 있듯이, 나쁜 것은 해야 할 일에 대한 손실입니다. 자유도가 1 개이므로 샘플 공간을 거의 탐색할 수 없습니다. 더 나쁜 것은 생성된 샘플이 1D 매니 폴드 (이 gif에 빨간색 점만큼 많은 회색 점이 있음)에 너무 밀집되어 있기 때문에 판별 기가 느슨해질 수 없으므로 실제 점을 식별하기 위해 열심히 노력할 필요가 없습니다. 가짜로부터, 그리고 그와 같이 생성기는 매우 유용한 정보를 얻지 못합니다 (그리고 용량이 있더라도 공간 채우기 곡선을 배우기에 충분하지 않습니다).

Figure 7: The distribution learned by the GAN from figure 6 after 30k training steps.

귀여운 작은 구불구불하지만 가우시안 분포는 거의 없습니다.
GAN은 완전히 30k steps 후에 맵핑을 배우는 것에 대해 실패했다. 이러한 관점에서 latent space를 2D, 3D,10D, 100D로 같은 아키텍처로 했을 때의 그림은 아래와 같다.

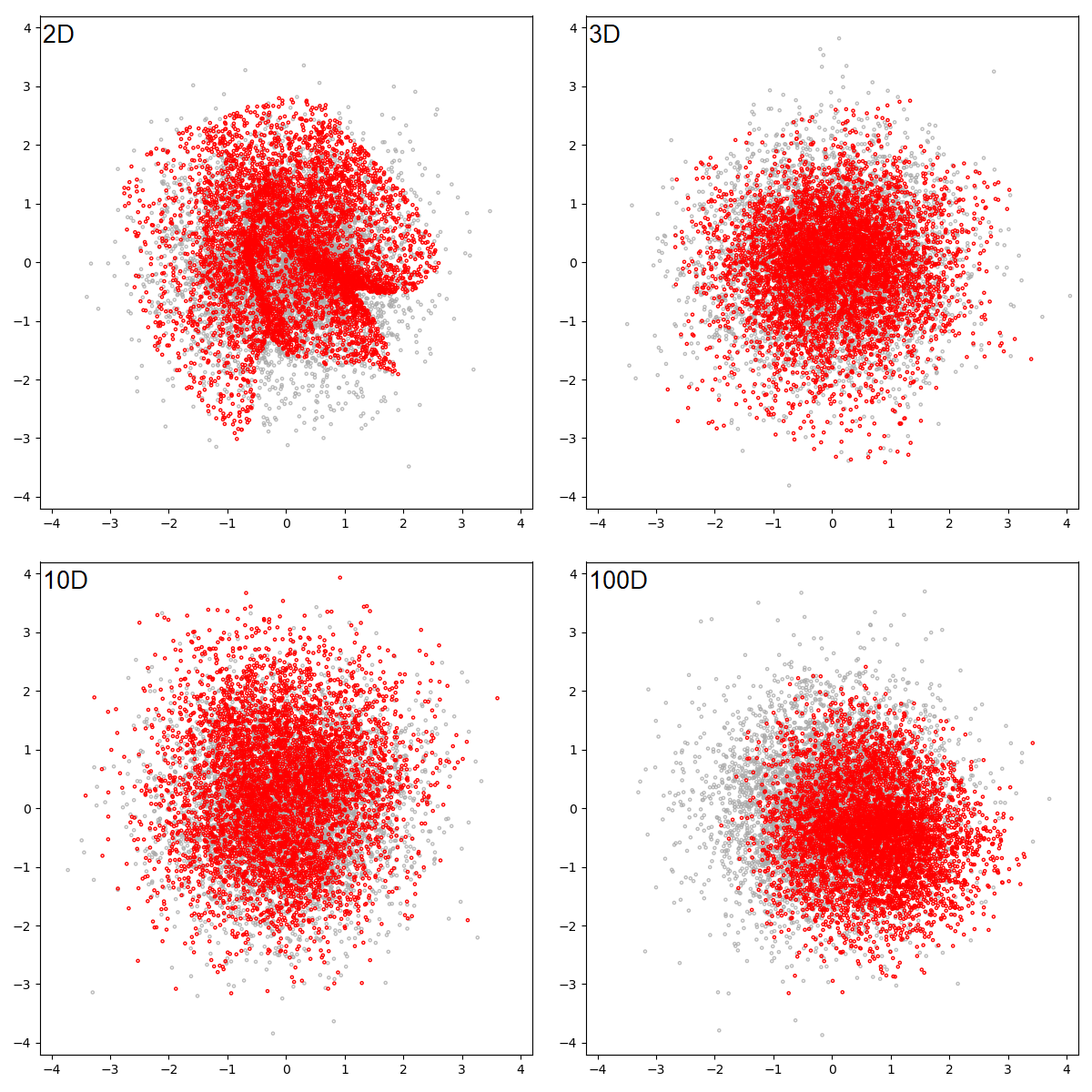
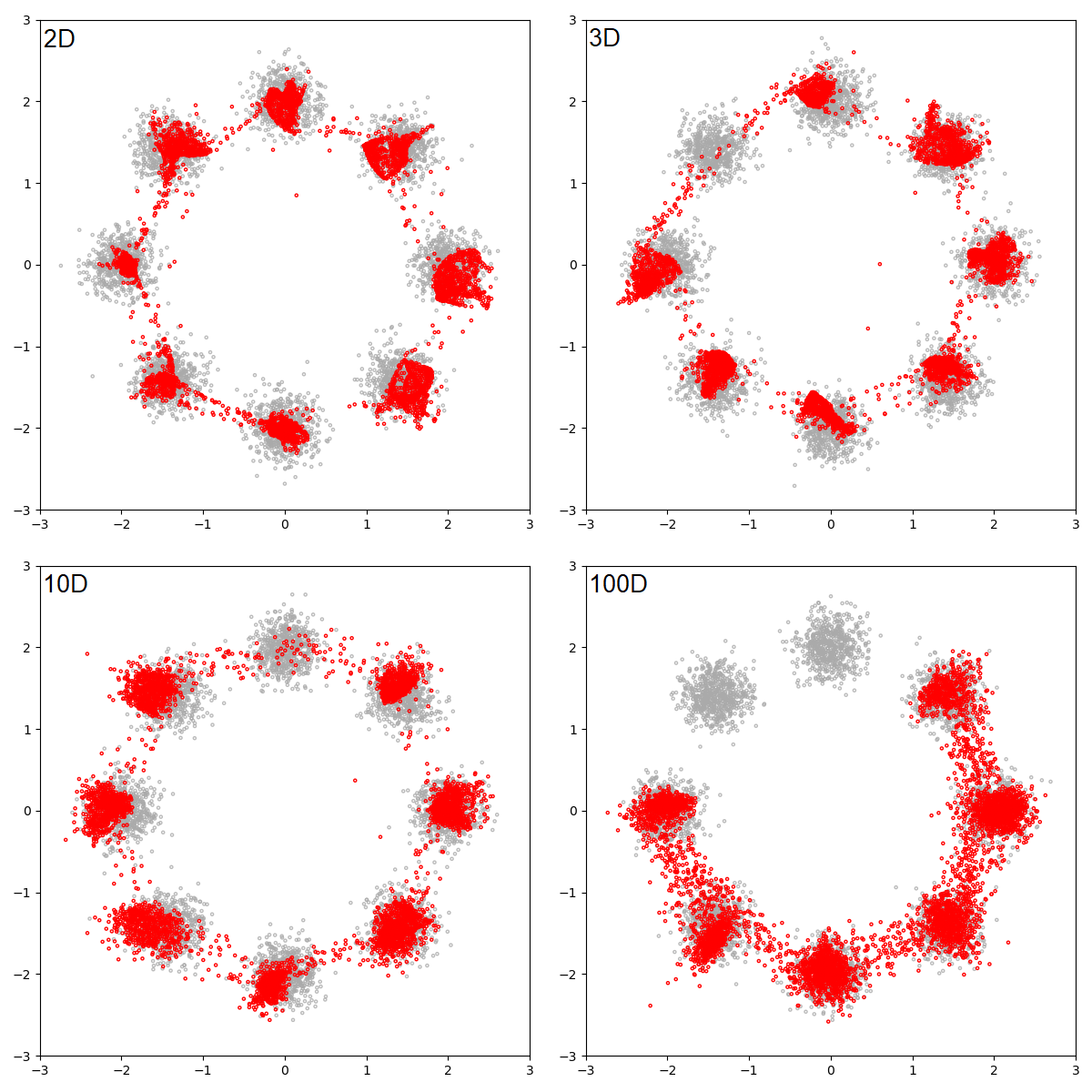
2D latent space GAN는 1D보다 훨씬 좋은 것을 나타내는 것을 알 수 있다, 그러나 여전히 대상 분포 근처에 없으며 몇 가지 명백한 꼬임이 있다.
3D 그리고 10D latent space는 납득 갈만한 결과를 만드는 것을 알 수 있다.
그리고  100D GAN은 거의 같은 분산을 가지지만 평균이 살짝 이동된 분포를 나타낸다. 
그러나 많은 균일 분포의 평균이 거의 정규 분포이기 때문에 고차원 GAN이  특정 문제에서 부정행위를 하고 있음을 명심해야 한다.

---

Eight Gaussians

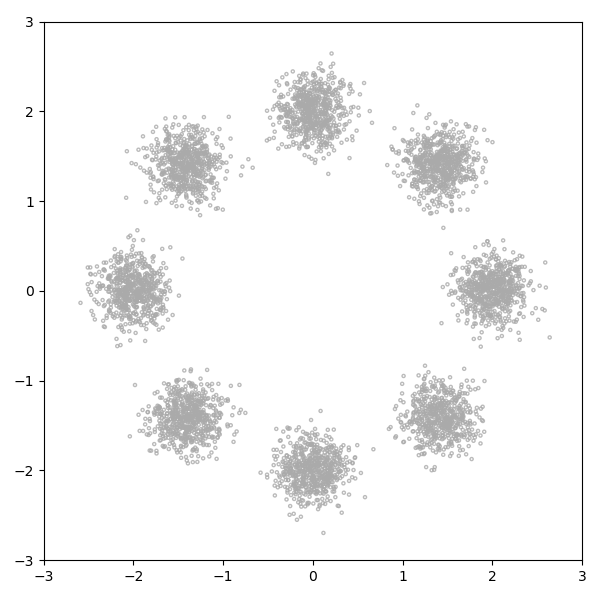
8개의 가우시안 분포이다. 이것은 2D Gaussian이 8개로 섞여 있다. 각각은 충분히 작은 분산을 가지고 절대 겹치지 않으며 공분산이 0이다. 
표본 공간이 2D이지만이 분포를 합리적으로 인코딩하는 것은 3차원에 있다.
첫 번째 차원은 별개이고 모드를 설명하고 (1에서 8까지 번호가 매겨 짐), 나머지 2개는 각각 해당 모드에서 x 및 y 변위를 설명합니다.

GAN의 latent dim을 1차원으로 했을 때 결과는 아래와 같다. 역시 잘 못하는 것을 알 수 있다.

Figure 10: A GAN with a latent dimension of 1 trying to learn the eight Gaussians distribution. Grey points are samples drawn from the true distribution, red points are generated samples. Each frame is one training step.

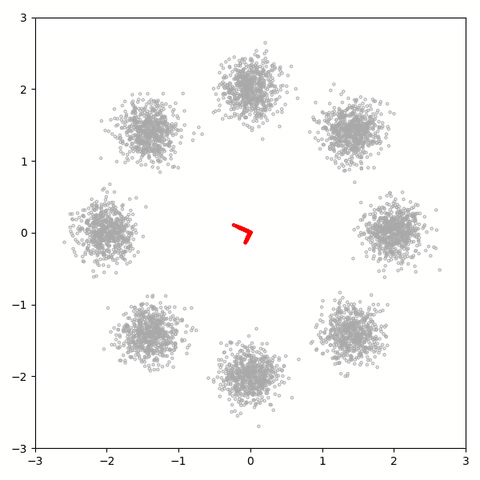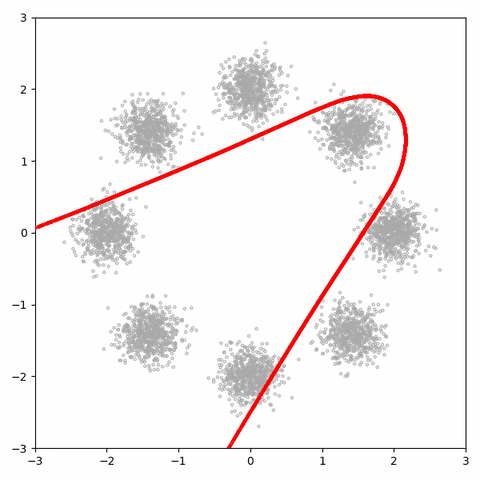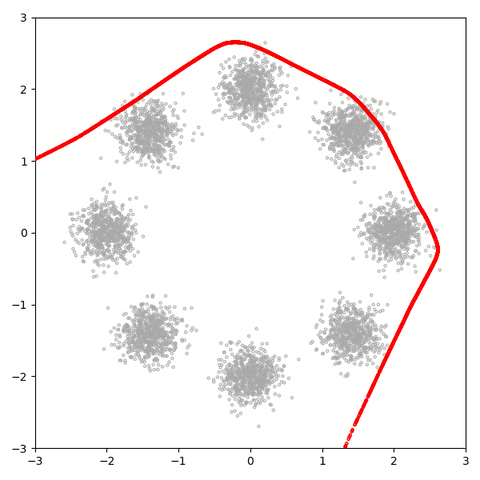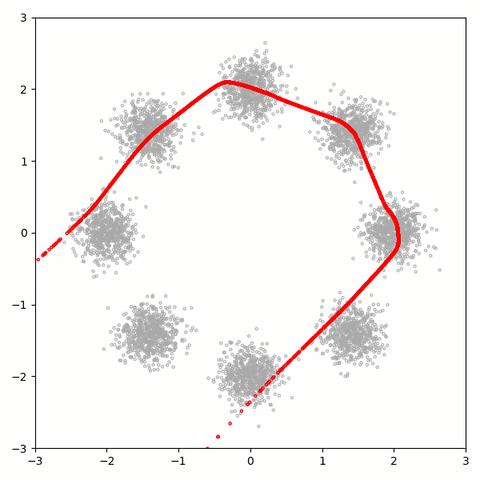
30k 학습 후에 배우는 분포는 다음과 같다.

Figure 11: The distribution learned by the GAN from figure 10 after 30k training steps.

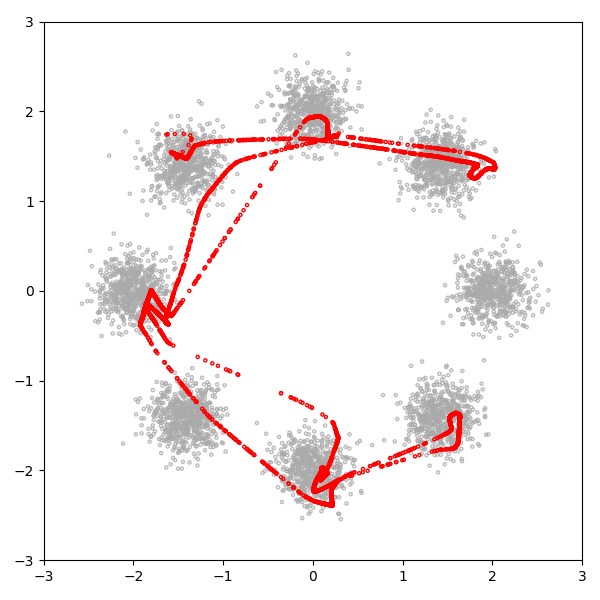
GAN은 1D 잠재 공간을 이 3D 분포에 매핑하는 데 어려움을 겪고 있다. 
가장 오른쪽 모드는 무시되고 모드 간에 상당한 수의 샘플이 생성되며 샘플은 정상적으로 분포되지 않다. 비교를 위해 잠복 크기가 2, 3, 10 및 100 인 30k 단계 후 4 개의 GAN을 더 고려해 봤다고 한다.

실제 분포와 학습된 분포 사이의 KL divergence를 실제로 측정하지 않고 어느 것이 가장 적합한 지 말하기 어렵습니다
(다음 글에서 한다고 하니 기대가 된다!)
그러나 저 차원 GAN은 모드 간 음수 공간에서 더 적은 샘플을 생성하는 것으로 보입니다.
위의 그림에서 흥미로운 것은 2D GAN은 model collapse가 보이지 않고, 3D~10D GAN은  mode collapse가 발생한 것을 알 수 있다. 그리고 100D GAN은 모드 2개에 대해서 샘플 생성하는 것을 실패했다.

> 차원이 최소환 같거나, 크게 해야 한다고 했는데, 너무 크게 하면 학습하기 너무 쉬워져서 그런지는 몰라도 mode collapse 현상이 발생해버리게 된다. (결국 trial & error이지만, 다차원 공간에서는 이것을 어떻게 파악할 수 있을지??)

---

Spiral

Figure 13: Spiral distribution. The distribution decreases in density as the spiral extends outward from the circle, and is uniform in density laterally across the arm

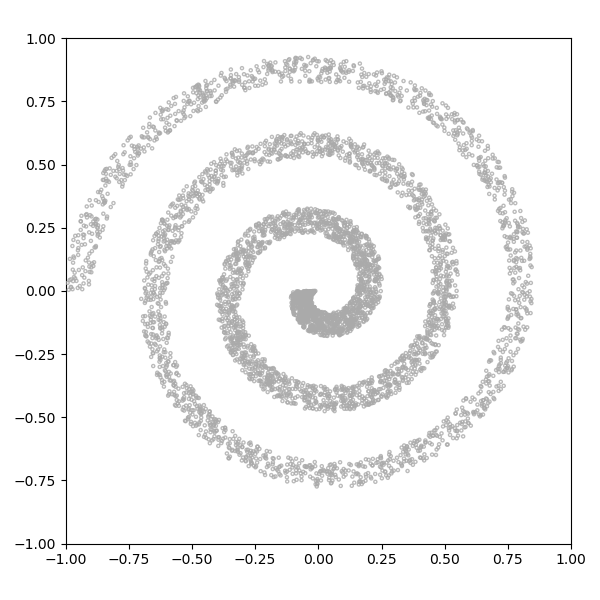
그림 13에 나와있는 나선 분포는 몇 가지면에서 8 가우스 분포보다 단순합니다. 길고 꼬임에도 불구하고 하나의 모드 만있는 GAN은 연속 입력을 불연속 화하지 않습니다. 하나는 나선을 따라 위치를 설명하고 다른 하나는 나선 내에서 측면을 설명하는 두 가지 차원으로 효율적으로 설명할 수 있습니다.

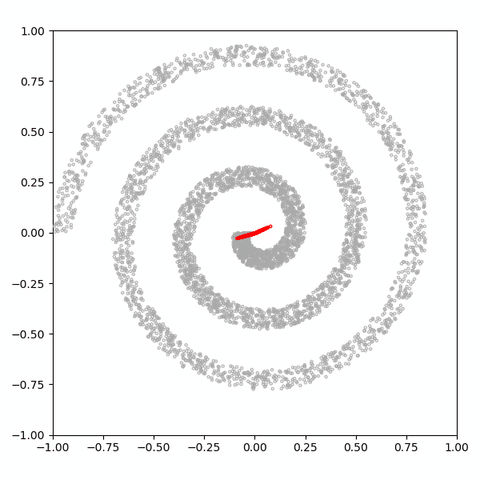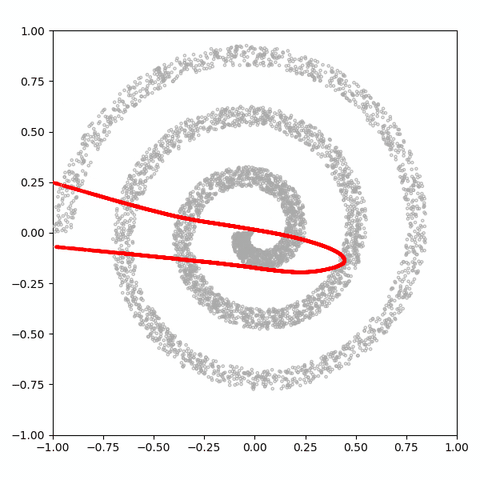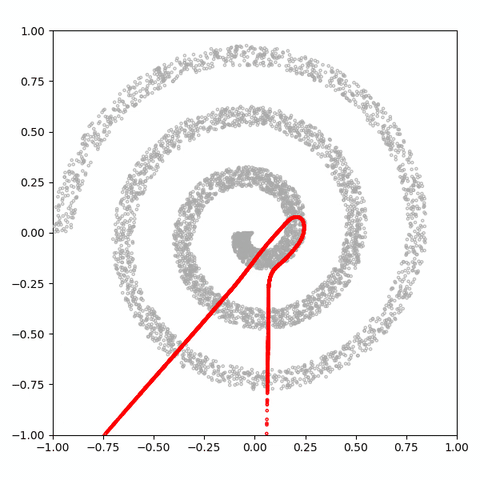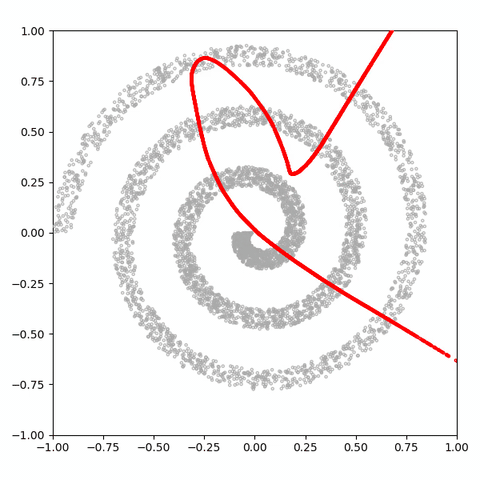
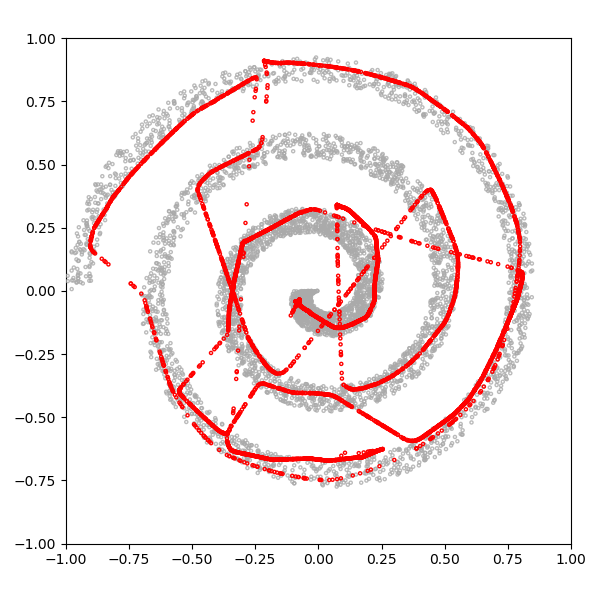
그러나 결과를 보면 GAN이 spiral 분포의 맵핑에 나쁜 성능을 내는 것을 알 수 있다. 
나선의 두 영역이 생략되고 네거티브 공간에 많은 샘플이 생성된다. 이 비효율적인 매핑 문제를 이전 글에서 자세히 다루므로 여기서는 다루지 않을 것이라고 한다. 대신, 2, 3, 10, 100의 잠재 크기로 30k 단계 후에이 분포를 학습하는 4 개의 GAN을 더 고려해 봤다.

다시 말하지만 KL 발산을 실제로 측정하지 않고 어느 것이 가장 좋은지 말하기는 어렵지만, 음의 공간에서의 커버리지, 균일 성 및 샘플링 양의 차이를 고려하는 것이 흥미 롭습니다.

 

---

Closing Thoughts

GAN fervor에 빠지고, 새로운 샘플을 꺼내기 위해서 연료로써 랜덤 수를 사용하는 매직 기계와 같이 취급하기도 한다.
도구의 작동 원리에 대한 이해는 도구를 효과적으로 사용하고 고장이 난 경우 문제를 해결하는 데 필수적입니다.
GAN을 사용하면 생성기가 일부 잠재 공간에서 일부 샘플 공간으로의 매핑을 학습하고 해당 학습이 어떻게 전개되는지 이해하고 있음을 의미합니다. 1D 분포를 고차원 분포에 매핑하는 극단적인 경우는 이 작업이 얼마나 복잡한지를 분명히 보여줍니다.

> 기존 NOISE 설정을 어떻게 할 지에 대해서 기본적으로는 너무 작게는 말고 인풋보다는 크지 않게 하는 식으로 하였는데, 그러한 생각에서 벗어날 수 있게 하는 좋은 글이었다.

 

 

https://towardsdatascience.com/why-do-gans-need-so-much-noise-1eae6c0fb177

Why Do GANs Need So Much Noise?

https://github.com/ConorLazarou/medium/blob/master/12020/visualizing_gan_dimensions/2_spiral.py

ConorLazarou/medium