Clova AI에서 Generative Model들에 대한 성능 지표 관련 논문임.
이미지 다차원 데이터에 대해서 지표 측정에 대해서 설명하는 것이라서, 읽어보고자 함.
1.Introduction
생성 모델을 평가하는 것은 어렵다. discriminative models $P(T|X)$이 쉽게 라벨링이 되어 있는 샘플 $(X_i,T_i)$에 대한 예측 성능을 측정하는 것과는 달리, generative models $P(X)$ 는 real $X_i$ 와 fake $Y_j$ 사이에 차별성을 측정한다. 복잡성을 더하여 각각의 단점성을 가지고 두 분포들 사이에서 거리를 측정하는 방법은 하나 이상이다.
심지어, Mean Opinion Score 같은 human judgement는 이상적이지 않다.
비록 트레이드오프 세트와 함께 몇 가지 정량적 지표가 제안되었다.
Fr´echet Inception Distance (FID) score는 가장 많이 사용되고 있는 지표이며, 경험적으로 인간 지각 점수 관련 good agreement를 제시했다.
그러나 FID는 두 분포의 비교를 하나의 숫자로 요약하여 생성 모델의 품질에 대한 두 가지 중요한 측면, 즉 fidelity와 diversity을 분리하지 못했다.
Fidelity는 진짜와 샘플이 닮은 정도를 의미하며, Diversity는 생성된 샘플이 실제 샘플의 전체 변동성을 포함하는지 여부를 측정한다.
유용한 평가 지표에 필요한 조건은
(1) 동일한 실제 및 가짜 분포를 검출할 수 있는 능력,
(2) 아우라이에에 대한 강건성
(3) mode dropping에 대한 반응성
(4) 평가 알고리즘의 하이퍼 파라미터 선택 용이성
4개라고 주장한다. 불행히도, 정밀도 및 회수 지표의 최신 버전조차도 요구 조건을 충족시키지 못한다.
그래서 CLOVA.AI분들은 density and coverage metric을 제안한다. 단순하지만 세심하게 설계된 매니폴드 추정 절차를 도입함으로써, fidelity-diversity 측정 기준을 경험적으로 신뢰할 수 있을 뿐만 아니라 이론적으로 분석할 수 있게 한다.
이미지 생성 알고리즘을 평가하기 위한 임베딩 알고리즘을 연구했다고 한다. 임베딩은 고차원성과 RGB 공간에서의 의미론 부족으로 인해 불가피한 성분이다. 중요함에도 불구하고, 내장 파이프라인은 기존 문헌에서 상대적으로 덜 연구되어 왔으며, 생성된 이미지의 평가는 대부분 ImageNet 사전 훈련 모델의 특징에 의존한다. 이는 때때로 공정한 평가를 제한하고 잘못된 개선 의식을 제공한다. 사전 교육된 모델에는 필연적으로 데이터 세트 편향이 포함되기 때문이다. 저자분들은 미리 훈련된 임베딩이 표적 분포가 자연적인 이미지 영역으로부터 멀어질 때 종종 예상치 못한 행동을 보인다는 것을 보여준다고 한다.
데이터셋의 편향을 배제하기 위해서, 저자들은 randomly initialized CNN feature extractor를 고려했다고 함. 우리는 무작위 임베딩이 분포의 불일치에 대한 더 거시적인 견해를 제공한다는 것을 관찰한다. 특히 랜덤 임베딩은 대상 데이터 분포가 ImageNet 통계와 상당히 다를 때 보다 합리적인 평가 결과를 제공한다.
Backgrounds
실제 분포 P(X)와 생성 모델 Q(Y)를 고려할 때 각각 ${X_i}$과 ${Y_j}$을(를) 샘플링할 수 있다고 가정한다. 표본 집합이 동일한 분포에서 얼마나 발생할 가능성을 평가하기 위한 알고리즘이 필요하다. 관련 분포 패밀리를 추적할 수 있고 전체 밀도 함수를 쉽게 추정할 수 있는 경우 통계적 시험 방법 또는 분포 거리 측정(예: Kullback-Leibler Divergence 또는 예상 우도)이 가능하다. 단, 데이터 P(X)가 복잡하고 고차원적인 경우(예: 자연 영상) 그러한 측정치를 순진하게 적용하기는 어려워진다.(Tesis et al., 2016).
이러한 어려움 때문에, 생성 모델의 표본 평가는 여전히 활발하게 연구되고 있는 주제다. 이 섹션에서는 기존 접근방식에 대한 개요를 제공한다. 우리는 이미지 생성 모델에 대해 가장 널리 사용되는 평가 파이프라인(제2.1조)을 설명한 다음, 충실도 및 다양성 측정에 관한 이전 저작물(제2.2조)을 소개한다.
2.1. Evaluation pipeline
raw 데이터에서 복잡 및 고차원 데이터 $X$를 통계적으로 분석하는 것은 어렵다. 그러므로, 이미지 생성 모델들의 평간 지표들은 다음과 같은 단계를 따른다.
- embed real and fake data $({X_i} and {Y_j})$ into a Euclidean space $R^D$ through a non-linear mapping f like CNN feature extractors
- construct real and fake distributions over RD with the embedded samples ${f(X_i)} and {f(Y_j)}$
- quantify the discrepancy between the two distributions.
Embedding
입력 공간에 대한 합리적인 지표를 세우는 것은 어렵다. 예를 들어 이미지 픽셀들 간의 $||X_i-Y_j||_2$의 $l_2$ 거리는 오해하기 쉽다. 왜냐하면, 인지적으로 2개의 동일한 이미지들은 큰 $l_2$ 거리(one-pixel translation) 생길 수 있다. 이 어려움을 극복하기 위해서, 연구자들은 feature space $||f(X_i)-f(Y_j)||_2$ 거리가 인간의 지각 측정지표에 대한 합리적인 대용치를 제공한다는 추론에 근거하여 많은 생성 모델 평가 지표들의 임베딩 함수 ImageNet pre-trained CNN feature extractor를 많은 생성 모델 평가 지표에서 내장 함수 $f$로 도입했다.
때문에 computing metrics를 위해 embedded 샘플들을 사용한다.
Building and comparing distributions
내장된 샘플 ${X_i}과(와) {Y_j}$을 고려할 때 많은 메트릭스가 (비) 모수 통계량 추정의 어떤 형태를 수행한다.
Parzen window estimates은 실제 샘플 {Xi} 주위에 가우스 커널이 있는 밀도 P(X)를 추정하여 가짜 샘플 {Yj}의 가능성을 근사하게 나타낸다. 모수적 측면에서 Inception Scores(IS)는 각 샘플 이미지 $Y_j$에 대한 1000 ImageNet 클래스에 대한 다항 분포 $P(T|Y_j)$를 추정하여 KL 분산과 추정된 한계 분포 $P(T)$를 비교한다.
FID는 X와 Y에 대한 평균 μ 및 공분산 Σ을 다변량 가우시안이라고 가정하여 추정한다.
2개의 가우시안의 차이는 Wasserstein-2 distance라고 알려진 the Fr´echet distance로써 계산이 된다.
2.2. Fidelity and diversity
IS나 FID와 같은 단일가치 측정지표는 생성 모델의 순위를 매겨 이 분야에서 흥미로운 진전을 이끌었지만, 진단 목적으로는 이상적이지 않다. 생성 모델의 중요한 관점 중에서 하나는 fidelity(각 인풋이 얼마나 현실적인지)와 diversity(얼마나 가짜 샘플들이 진짜 샘플들 사이의 변동을 포착하는지) 사이에서 trade-off이다.
두 가지 특성을 별도로 포착하는 두 가지 가치 지표(precision 및 recall)의 변형을 소개한다.
Precision and recall
precision 및 recall는 두 생성 모델이 FID 점수가 비슷한 반면, 질적 fidelity와 diversity 결과는 다른 병리학적 사례를 보고하였다.
precision는 대략 P(X)에 의해 생성될 수 있는 Q(Y)의 부분으로 정의되며, recall은 Q(Y)에 의해 생성될 수 있는 P(X)의 부분으로 대칭적으로 정의된다. 이러한 개념은 유용할지라도, 실제적으로 적용할 때 단점이 존재한다.
임베딩 공간은 균일하게 밀도가 높고, 초기화에 민감한 k-평균 알고리즘에 의존하여 지원 추정을 하며, 측정지표로서 무한대의 값을 산출한다고 가정한다.
Improved precision and recall
(Kynk¨a¨anniemi et al., 2019) 는 위에서 언급한 단점을 해결하기 위해 향상된 prcesion과 recall을 제안한다.
확률 밀도 함수는 균일 밀도 가정과 k-평균 알고리즘에 대한 의존도를 극복하면서 k-가장 가까운 인접 거리를 통해 추정한다.
P&R은 먼저 P(X)와 Q(Y)에 대한 "매니폴드"를 별도로 구성하며, 객체가 1에 합치하지 않는 것을 제외하고 확률론적 밀도 함수와 거의 동일하다. 그런 다음 precision는 가짜 샘플의 예상 가능성을 실제 매니폴드에 대해 측정하고, 실제 샘플의 예상 가능성을 가짜 매니폴드에 대해 측정한다.
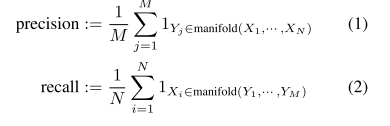

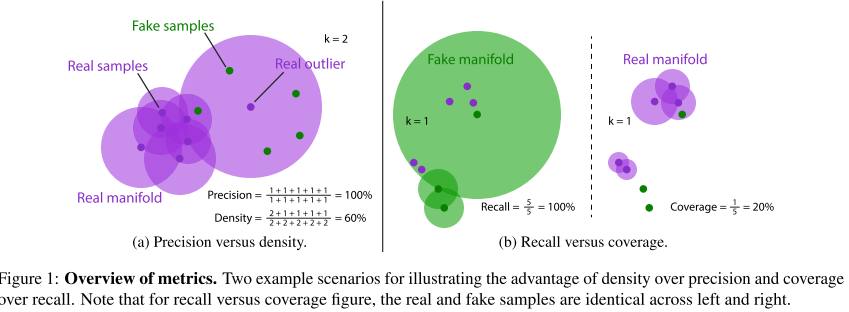
where $B(x, r)$ is the sphere in R^D around x with radius r. $NND_k(X_i)$ denotes the distance from $Xi_$ to the $k^{th}$ nearest neighbour among ${X_i}$ excluding itself. Example computation of P&R is shown in Figure 1.
3. Density and Coverage
저자분들은 precision과 recall에 고나한 문제를 완전히 해결할 수 있는 실용적으로 사용 가능하고 참신한 지표인 density and coverage (D&C)를 제안한다고 한다.
3.1. Problems with improved precision and recall
improved precision and recall (P&R)는 여전히 아웃라이어와 비효율성에 취약하게 구성되여졌다.
Equation 3에 있는 nearest neighbor manifolds를 구축는 것은 각 표본 주위의 구가 반경 또는 인접 표본의 상대 밀도에 따라 정규화되지 않기 때문에 신중하게 수행해야 한다.
따라서 가장 가까운 인접 매니폴드는 일반적으로 아웃라이어 주변의 진정한 매니폴드를 과대평가하여 실제로는 바람직하지 않은 효과를 초래한다.
to be continued...



'관심있는 주제 > GAN' 카테고리의 다른 글
| Stock Market Prediction Based on Generative Adversarial Network - 리뷰 (0) | 2020.04.09 |
|---|---|
| GANs for tabular data - 리뷰 (1) | 2020.03.29 |
| A Novel Framework for Selection of GANs for an Application -논문 리뷰 (0) | 2020.03.08 |
| Why Do GANs Need So Much Noise? - 리뷰 (0) | 2020.03.03 |
| Self-Attention Generative Adversarial Networks - 설명 (0) | 2020.02.16 |