Tricks for Manipulating Probability - 리뷰

확률 값에 대해서 더 잘 처리하는 것이 필요하다고 생각은 하지만, 실제 관련 글을 우연히 찾게 돼서 읽어 보기로 하였다.
머신 러닝이나 인공 지능의 근본적인 문제를 해결하기 위해서는 확률의 기교가 필요하다.
저자의 블로그는 계산을 더 쉽고 때로는 심지어 가능하게 만들기 위해 서로 다른 확률 문제에 적용된 다양한 기술들을 종합하는 것을 목표로 한다!
이 블로그는 확률과 기댓값에 대한 기본 이해를 가정한다. 

 

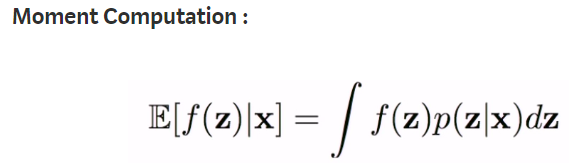
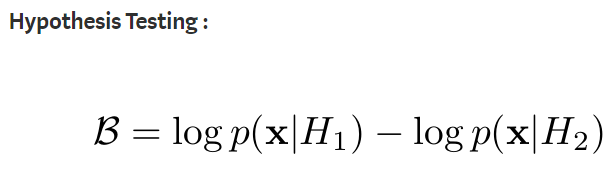
1. Identity Trick 

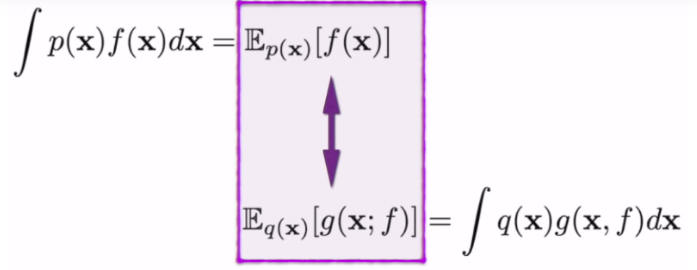
This transforms an expectation of f(x) 
p(x)f(x) 를 q(x) g(x, f)로 바꿔서 푸는 것이다. 

Bayes's formula안에서 Evidence Calculation 은 다차원 변수에서 풀기 어려운 문제다. 
Generative Model에서, p(x)를 계산하는 것은 주요 목적이다. 여기서 x는 sample이고 z는 latent variable 그리고 p(x|z)는 z가 주어졌을 때 관측되는 x의 likelihood이다. 
아래의 식은 z에 대해서 p(x,z)를 marginalisation 한 것이다.

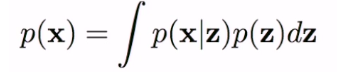
p(z)는 잠재된 latent variable의 실제 분포이다. 그러므로 그것을 다루는 것은 어렵다. 
그러므로 다른 분포 p(z)를 근사할 q(z)를 도입한다. 그리고 이것에는 훌륭한 수학적인 성질들들이 있다.
Sampling은 q(z)로부터 뽑기 쉽다. 그리고 많은 경우 가우시안 분포로 한다. 
우리는 간단히 q(z)를 곱하고 나눠서 q(z) 기댓값으로 변경할 수 있다.

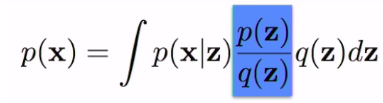
• 조건 
  
  
  • q(z) > 0 , when p(x|z)p(z) != 0
  • q(z)는 알려지거나, 다루기 쉬워야 한다.

우리는 q(z)가 샘플링하기 쉬운 것으로써 Monte Carlo Sampling Methods를 사용하여 기댓값을 계산할 수 있다.

---

Bounding Trick 에서 문제를 해결하는 또 다른 방법에 대해 논의할 것이다.

Identity Trick elsewhere

• Manipulating stochastic gradients.
• Derive probability bounds.
• RL for policy correction.

2. Bounding Trick :

이 트릭은 convex analysis로 부터 온다. 적분의 bound값을 이용한다 Jensen's Inequality

대부분의 ML 문제들에서, 추가적인 성질과 엄격한 오목 성 때문에 함수 f를 logarithmes를 사용할 수 있다. 

Other Bounding Tricks:

• Fenchel Duality.
• Holder’s inequality.
• Monge-Kantorovich Inequality.

변분추론에서 Evidence Lower Bound(ELBO) 추정을 나타낸다. 
첫 번째 Trick에서 Evidence Calculation의 Monte Carlo의 추정 대신에 최적의 lower bound를 찾기 위해서 Jensen's Inequality를 사용한다.

Jensen's Inequality를 사용하여 log를 취한다.

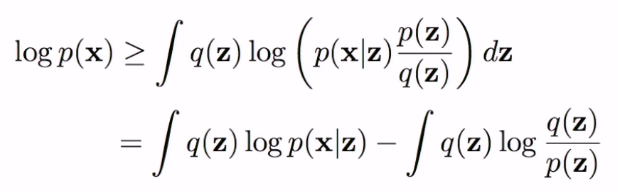
RHS는 Variational Lower Bound이다.

• The first term is the reconstruction loss. 
• the second term is the KL Divergence between the introduced approximate family of distribution over the latent variable, q(z) and the original p(z).

첫 번째 텀은 p(x|z)의 분포에 의존해서 l2 loss 또는 cross-entropy loss 형태들이다. 
그리고 이 문제는 Expectation Maximisation 알고리즘을 사용하여 최적화할 수 있다. 

3. Density Ratio Trick

종종 확률 밀도의 비율이 필요할 때, 비율을 계산하는 순진한 방법은 양쪽을 계산하고 나서 비율을 취함으로 써이다.
이 트릭은 두 확률 밀도들의 비율은 두 분포로부터 뽑은 샘플들을 사용하여 분류기에 사용하여 계산한다.

It is given by the following equation where p*(x) and q(x) are the two probability distributions and p(y=1|x) & p(y=-1|x) is the classifier.

 

 

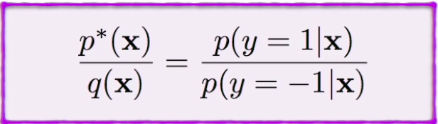
동등한 세팅에서 

균등한 데이터셋에서 p(y=+1)과 p(y=-1)과 동등하므로 다음과 같이 간단하게 할 수 있다.

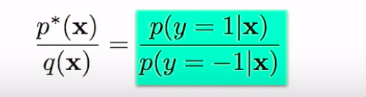
Density Ratio Trick elsewhere:

• Generative Adversarial Networks (GANs).
• Noise contrastive estimation.
• Two-sample testing.

Next, we look at the tricks used in manipulating the gradients of expectation of some function f.
아래에 매우 흔한 gradient 문제는 통계적인 과학에서 나타난다. 
분포 q(z)가 간단하고 적분이 1이라면, 기대치는 계산이 되고 gradient도 계산할 수 있다. 
그러나 일반적인 프레임워크에서 우리는 closed form을 계산할 수 없다.
그러므로 gradient를 계산하는 것은 중요하지 않은 문제가 된다.

Here, Φ and θ are the parameters of q(z) and f(z) respectively.

기대치를 통합형태로 표현하면 이 gradient 추정에 접근하는 두 가지 방법이 있음을 알 수 있다.

1. Differentiate the density q(z) : (Score-function estimator)
2. Differentiate the function f(z) : (Pathwise estimator)

이 2가지가 어떻게 작동하는지 볼 것이다. 
gradient 추정 문제를 공식화할 수 있고 트릭으로 풀 수 있다. 

Before that, these are the typical areas in which the above problem appears:

• Generative models and inference.
• Reinforcement learning and control.
• Operation research.
• Monte Carlo Simulation.
• Finance and asset pricing.
• Sensitivity estimation.

4. Log-Derivative Trick :

첫 번째 접근은 q(z)의 미분하는 것이다 그것은 Score Function Estimator로 불린다.
통계에서 `score`는 무엇인가?
score (informant)는 파라미터 vector에 대한 log(L(theta)) 로그 가능도 함수의 gradient이다.

(Here,  ϕ  is the  parameter,   q  is the  likelihood function, and the gradient is w.r.t. ϕ )

score function의 성질은 다음과 같다.

1. score function의 기댓값은 0이다. (Jensen's inequality)

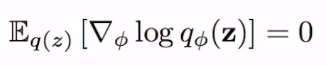
2. score function의 분산은 Fisher Matrix로써 주어진다. 

stochastic 최적화의 문제를 풀기 위해 위의 트릭을 어떻게 사용되는지 알아보자.

In the figure given below,
1. The gradient is w.r.t. ϕ and the order of integration and gradient can be interchanged.
2. The gradient of q(z) is taken and identity trick is applied by multiplying and dividing with q(z).
3. Log derivative trick comes into play.
4. The gradient of the shown expectation is transformed into an expectation of the shown function.

상수 c는 변하지 않는다 이것은 성질 중에서 score function의 기댓값은 0이라는 것을 사용하는 것이다.
그러나 f(z)로부터 특정 상수 c를 빼는 것은 gradient의 분산을 감소시킨다. 
Now, we are ready to derive the Vanilla Policy Gradient in Reinforcement Learning.

• A trajectory is a sequence of states and actions in the world.

• The goal of the agent is to maximise some notion of cumulative reward over a trajectory, known as a return.
• One kind of return is the infinite-horizon discounted return, which is the sum of all rewards ever obtained by the agent but discounted by how far off in the future they are obtained. This formulation of reward includes a discount factor γ ∊(0,1):

• Another kind is the finite-horizon undiscounted return, which is just the sum of rewards obtained in a fixed window of steps. We will use this in our derivation.

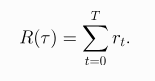
• A policy π is a rule used by an agent to decide what actions to take. It may be stochastic. The π in the below equation signifies the distribution of probability over actions in a given state. We often denote the parameters of such a policy by θ,

• Let’s suppose that both the environment transitions P and the policy π are stochastic. In this case, the probability of a T-step trajectory given the policy π is:

• The Log-Derivative Trick :

• The log-probability of a trajectory is just :

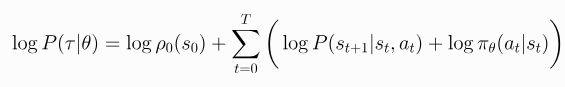
• The gradient of the log-probability of a trajectory is thus :

• Note that the environment has no dependence on θ, so gradients of initial state probability ρ and transition probability P are zero.
• The expected return is denoted by:

The goal in RL is to select a policy which maximises the expected return J(π) when the agent acts according to it. The central optimisation problem in RL can then be expressed by :

where, π* is the optimal policy.

We would like to optimise the policy by gradient ascent, like

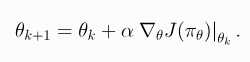
∇J(π) policy 성능의 gradient는 policy gradient라고 불린다. 
이 방식에서 policy를 최적화하는 알고리즘은 policy gradient algorithms이라고 불린다. 

어떤 policy gradient 기반한 핵심 아이디어는 높은 return으로 이끌게 행동의 확률을 강요하게 하는 것이다.
그리고 최적의 policy에 도착할 때까지 낮은 return으로 하게 하는 행동의 확률을 낮추도록 한다.

이 식은 샘플 평균으로 추정된다. 만약 trajectory들을 모은다면 policy gradient는 다음과 같이 추정된다.

5. Reparametrisation Trick :

Variational AutoEncoder에서 다룰 때 이 트릭을 봤을 것이다.
모든 분포는 다른 분포의 변형으로서 표현될 수 있다. 
이것의 한 예는 모든 균일한 분포가 우리가 관심 있는 분포의 역 CDF로 변환될 수 있다는 역 샘플링 방식이다.
일반적으로 p(z) 분포는 다른 분포 p(ε)로부터 변형된다. 

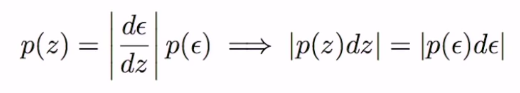
stochastic 최적화의 두 번째 방법으로 돌아가면, 우리는 경로적인 추정자 또는 재방문 속임수를 가지고 있다. 이번에는 f(z)를 조종할 것이다.

z는 q(z)로부터 샘플링된다. p(ε)를 도입해서 함수 g는 위의 식처럼 정의된다. 우리 문제에서 z를 대체하는 것은

Both of the above methods help in converting the gradient of expectation into an expectation of some gradient which can further be approximated or efficiently calculated using Variational method or Monte Carlo method.

음.... 모르겠다

https://towardsdatascience.com/tricks-for-manipulating-probability-470b7eb7dfd

Tricks for Manipulating Probability