The Synthetic data vault - 논문리뷰

2016년 논문이지만, Table data 생성에 대해서 접근한 논문인 것 같아서 읽어보려고 한다!

사실 여기선 SDV에 대해서 설명을 하지만, 크게 관심은 없다.

합성 데이터를 어떻게 평가하는지 왜 그렇게 평가해야 하는지 그런 것에 초점을 맞추려고 한다.

# Abstract

Synthetic Data Vault라는 것을 제안한다. SDV란 관계형 데이터베이스를 생성하는 모델이다. 

 

# Introduction

수많은 이해관계자들과의 대화에서, 우리는 사생활 문제로 인해 데이터를 공유할 수 없는 것이 종종 기업이 외부의 도움을 받는 것을 방해한다는 것을 발견했다.

심지어 기업 내에서도 데이터 접근을 제한하는 요인에 의해 개발 및 시험이 저해될 수 있다.

 

이 논문 역시 Synthetic data를 생성함으로써, 앞에서 말한 문제를 해결하려고 한다.

Synthetic data 에는 2가지 필수요건을 만족해야한다.

1. 현실성을 보장하고 데이터 과학자의 관심을 끌기 위해서는 통계적으로 원본 데이터와 어느 정도 유사해야 한다.
2. 그것은 또한 형식적이고 구조적으로 원래의 데이터와 유사해야 한다. 그래서 그 위에 쓰인 어떤 소프트웨어도 다시 사용할 수 있다.

이 2가지를 만족하기 위해서는, 데이터는 통계적으로 원본 형태 안에서 모델링이 되어야 한다. 

그래서 이것을 통해 샘플링도 하고, 재생산도 한다.

예를 들어 다변량 분포로써 공변량을 모델링하거나 공변량들 공간 안에서 Synthetic data를 생성하고 샘플링한다.

 

과거에 몇몇 연구자들은 형상 공학이나 통찰력 창출을 목적으로 관계형 데이터베이스에서 통계적으로 데이터를 모델링하는 데 주력했다. 

그것은 관계 데이터 모델에 베이 시안 네트워크를 배치했고, 그러한 관계의 교차점에서 조건부 데이터 조각에 대한 매개변수를 배웠다.

 

이 두 가지 개념을 확장함으로써 우리는 통찰력이 아니라 풍부한 합성 데이터라는 다른 목표를 가진 다단계 모델을 개발한다.

 

통계적으로 유효한 모델을 만들고, 우리는 또한 자료의 뉘앙스에 주목해야 하고, 그것들을 모방해야 한다.

 

예를 들어, 누락된 값을 여러 가지 방법으로 처리하고 범주형 값과 데이터 시간 값을 처리할 수 있는 기능을 구축했다.

 

 

 

 

Summary of results

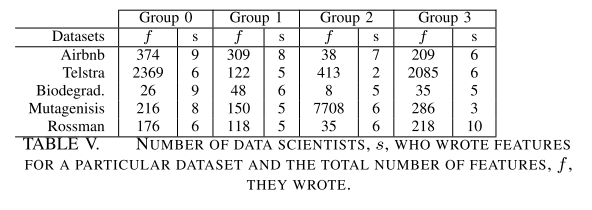
5개의 다른 데이터 셋을 모델링하고, 합성된 데이터 3가지 버전을 만든 다음에 39명의 데이터 과학자를 고용해서 진행했다. 그래서 예측 문제를 해결하기 위해 그룹을 나눴다. 

각각의 데이터셋에서 예측 결과를 비교했다. 

 

We found no significant statistical difference in the data scientists’ work

데이터 과학자는 생성된 데이터로 기존의 데이터와 성능이 비슷하거나 더 높은 것을 만들었다.

 

The level of engagement with synthetic data was high

특별히 데이터에 대해서 합성인지 아닌지 말하지 않고 진행을 했는데, 데이터를 의심 없이 5개의 데이터셋을 잘 활용했다고 한다.

 

synthetic data를 생성하는데 이해하기 위해서, 시각화나 설명 분석보다는  예측 모델링을 선택했다고 한다.

몇 가지 이유가 있다고 한다.

1. 영향
2. 피쳐 엔지니어링의 기초적인 병목현상을 넓힐 수 있는 가능성,
3. 과거 경험으로부터 많은 관찰.

• 데이터베이스가 주어질 때, 데이터 과학자들은 종종 기능에 대한 소프트웨어를 정의하고 쓰기 위해 뛰어들기 전에 각 테이블의 처음 몇 행만 본다.
• 만약 데이터가 데이터 과학자의 일상적인 활동과 관련된다면, 그들은 먼저 그 분야를 이해하려고 시도하고 그러고 나서 재빨리 소프트웨어를 쓰기 시작할 것이다.
• 데이터 과학자는 예측 모델링에서 첫 번째 합격 후 데이터를 심층적으로 탐구할 가능성이 높으며, 특히 그러한 합격으로 예측 정확도가 높지 않은 경우 그러하다.

이유를 보니 나도 이런 식으로 하는 것 같고, 그래서 공감이 간다

 

 

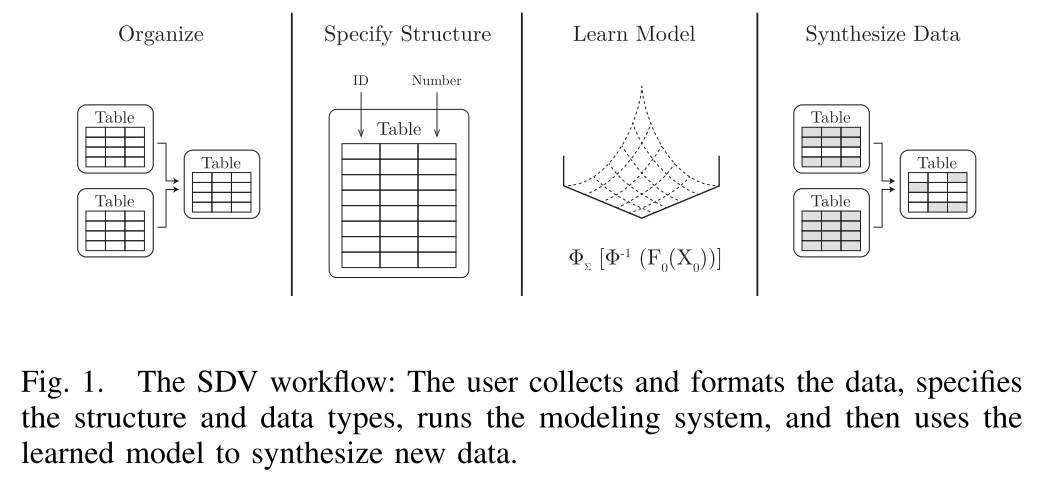
다음 4단계를 따른다.

 

1. Organize
   • SDV에 데이터를 공급하기 전에 사용자는 데이터베이스의 데이터를 각 표에 하나씩 별도의 파일로 포맷해야 한다.
2. Specify Structure
   
   • 사용자는 각각 테이블의 구조에 대해서 기본 정보를 구체화해야 한다. 그리고 데이터 베이스를 위해 metadata를 생성해야 한다. 
   • ID 정보 변수들은 특별하다. 왜냐하면 그것들에는 multiple tables에 대한 정보를 포함하고 있기 때문이다. 
3. Learn Model
   • 그런 다음 사용자는 SDV의 스크립트를 호출하여 생성 모델을 학습한다.
   • SDV는 표 사이의 관계를 설명하도록 설계된 모델링 알고리즘을 사용하여 순차적으로 표를 반복한다.
   • SDV는 각 테이블에서 의존성 구조를 발견한다고 한다.
4. Synthesize Data
   
   •  

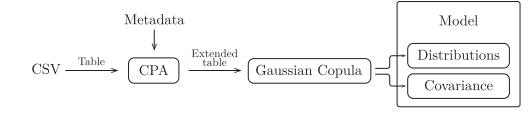
• 우리는 독립 실행형 테이블을 다른 데이터와 독립적으로 모델링하고자 하는 행과 열의 집합으로 정의한다.
• 독립 실행형 표의 생성 모델은 숫자 데이터를 나타내는 모든 열을 포함하며, 1은 다음과 같이 구성
  
  • Distributions: The probability distributions of the values in each column 
  • Covariances: How the value of a column affects the value of another column in the same row

Distribution은 각 칼럼을 보는 것이고 Covariate는 그들의 의존성을 설명한 것이다.

 

Distribution : 생성 모델은 각각의 칼럼들의 아는 분포의 모양에 의존한다. 이 분포의 shape은 cdf function으로 나타낸다.  이때는 이것을 계산하는 것이 꽤 어려웠나 보다. 그래서 가우시안으로 해서 mu, sigma로 이용했다고 한다. 가우시안뿐만 아니라 다른 여러 가지로 했는데 Truncated Gaussian Distribution , Uniform , Beta , Exponential 

만약 칼럼이 가우시안이 아니면, 다른 분포로 하는 게 낫다. 여기선 Test 하기 위해서 KS로 한 다음에, P-value로 측정을 하려고 한다. 현재는 Wasserstein distance도 있고 cramer distance도 있다고 한다. 

 

Covariance : 분포 외에도 생성 모델은 기둥 사이의 공분산도 계산해야 한다. 그러나 분포의 모양은 불필요하게 공분산 추정치에 영향을 미칠 수 있다.

이러한 이유로 우리는 the multivariate version of the Gaussian Copula 눈을 돌린다. 
Gaussian Copula는 공분산을 찾기 전에 모든 열 분포를 표준 정규 분포로 변환하여 분포 모양이 유도할 수 있는 모든 편향을 제거한다. 

Gaussian Copula

1. We are given the columns of the table 0, 1,... , n, and their respective cumulative distribution functions F0,... , Fn
2. Go through the table row-by-row. Consider each row as a vector X = (x0, x1,... , xn).
3.  

4. After all the rows are converted, compute the covariance matrix, Σ of the transformed values in the table.

B. Relational Table Model

Fig. 4. An illustration of CPA for a row in table T with primary key “33”. Tables A, B, and C refer to table T, so the lookup yields 3 sets of conditional data. Each is modeled using the Gaussian Copula, yielding conditional parameters.

 

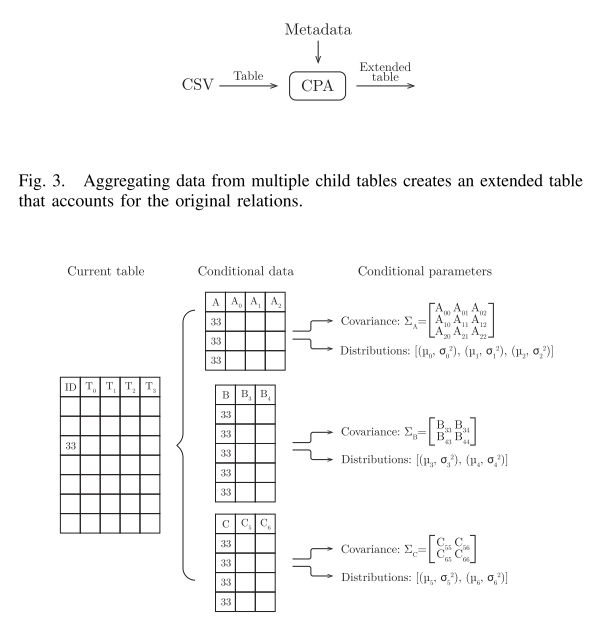
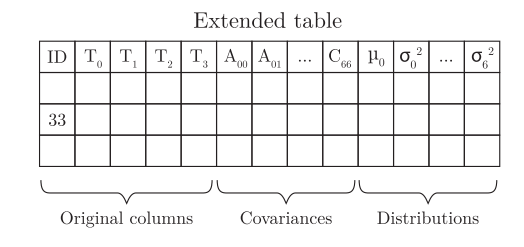
이렇게 한 다음에  연장된 테이블의 생성 모델을 생성하기 위해 Gaussian Copula process를 사용한다.

이 모델은 original 칼럼들 사이에 공변량들을 포착할 뿐만 아니라, 원본 테이블의 조건부 변수들의 의존성도 잡을 수 있다.

 

C. Pre-Processing

일단 이러한 Gaussian Copula와 CPA는 Missing이 없다는 가정에서 한다.

만약 Missing이 있다면, 전처리는 필수적이다!

데이터 타입에 따라 결국 다양한 미싱 처리를 해야 한다. 

예를 들어, 결측 값이 있는 datetime인 열은 먼저 범주형 및 datetime 유형의 두열로 변환된다.

그런 다음, 범주형 열과 기간 열은 추가로 숫자 열로 변환된다.

1) Missing Values:

미싱이 있을 경우 이것 또한 정보가 있는 것이기 때문에 함부로 무시할 수가 없다.

미싱에도 몇 가지 종류가 있는데,

• Missing not at random(MNAR)
  • 데이터가 누락된 것은 예정된 것 때문이다.
  • 만약 몸무게로 예를 들 경우, 과체중인 사람은 쉽게 자기 몸무게를 별로 알리기 싫을 것이다. 이때 미싱은 몸무게가 높을 때 자주 발생할 것이다.
• Missing at random(MAR)
  • 다른 row와 연결된 데이터에서의 누락이다.
  • 예로서 아마 여성은 자기 몸무게를 알리기 싫을 것이다. 그래서 여성이라는 다른 변수의 특성으로 인해 몸무게라는 변수가 누락돼서 서로 연결되어 있는 관계
• Missing Completely at random(MCAR)
  • 우연히 그냥 없어진 경우, 기계 결함 같은 것들

결국 여기선 MCAR를 제외하고는 미싱 자체가 중요한 정보를 담고 있다. 

합성된 데이터도 결국 원본처럼 미싱을 담으면서 생성을 시켜야 한다. 

 

마지막 경우에는 누락된 값이 반드시 필요한 것은 아니다.
수치적인 관점에서 고려되지만 SDV는 이것이 사실일 수 있다는 것을 알지 못한다. 따라서, 세 번째 사례가 무작위로 완전히 누락되더라도, SDV는 모델을 만들어야 한다.

 

When the SDV encounters any column that has at least 1  missing value, it replaces the column with two columns:

 

• 동일한 유형의 열, 누락된 값이 동일한 열의 누락되지 않은 값을 임의로 선택하여 채워진 열.
• 원본 데이터가 있는 경우 "예"를, 해당 행에 대한 데이터가 없는 경우 "아니오"를 포함하는 범주형 열.

 

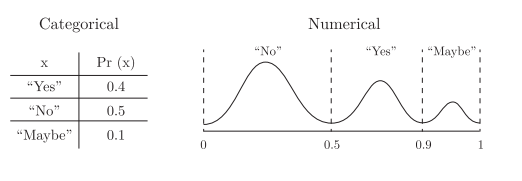
2) Categorical

cateogrical 변수는 Gaussian copula or CPA로는 모델링이 되지 않는다.

결국 여기서 사용한 방법은 이것을 Numeric으로 바꿔준 후 0~1 사이로 변경을 한다.

개인적으로 이것을 나도 사용하고 있어서 뿌듯했다 ㅎㅎㅎ

 

 

1. Sort the categories from most frequently occurring to least.
2. Split the interval [0, 1] into sections based on the cumulative probability for each category.
3. To convert a category, find the interval [a, b] ∈ [0, 1] that corresponds to the category.
4. Chose value between a and b by sampling from a truncated Gaussian distribution with µ at the center of the interval, and σ = b−a /6
   

Fig. 6. The method that converts categorical variables to numerical data. Based on the proportions, “No” is assigned the interval [0, 0.5]; “Yes” is assigned [0.5, 0.9], and “Maybe” is assigned [0.9, 1]. Each occupies its allocated interval with a Gaussian distribution.

D. Database Modeling

 

이 부분은 내가 관심 있는 부분이 아니니 패스!

 

Results!

아까 모델 기반으로 한다고 했으니 변수를 해석할 때 2가지를 볼 것이다.

1. Accuracy : 오리지널과 얼마나 차이가 나는지?
2. Qualitative findings : 데이터 사이언티스트들 진짜와 가짜를 혼동하지 않을 것인가?!

 

Accuracy

Was there any significant difference between the features generated with synthetic data and those generated with the original dataset? To test this, we followed these steps

 

1. We computed every feature script written by a data scientist on the original training dataset (the control).
2. Once the feature was extracted, we computed its predictive accuracy by training a classifier with the feature alone and evaluating 10-fold cross validation accuracy on the training dataset.
3. We then grouped these accuracy numbers into 4 subsets. The first set contained all the accuracy numbers for features written using the control data. We call this S0. The second set contained accuracy numbers for features written on top of no-noise data S1, the third set was table noise S2 and the fourth set was key noise S3. (Note that all feature values were calculated on the control dataset.)
4. We then performed the two-sample t-test between three pairs (S0, S1), (S0, S2) and (S0, S3). The two sample t-test returns a test decision for the null hypothesis that the data in vectors S0 and Si comes from independent random samples from normal distributions with equal means and equal but unknown variances. The alternative hypothesis is that the data comes from populations with unequal means. The result is a logical value.
   1. If Result = True, it indicates the rejection of the null hypothesis at the α significance level.
   2. If Result = False, it indicates a failure to reject the null hypothesis at the α significance level

Qualitative Findings

in particular, we observed the questions different data scientists asked to determine whether they were confused by the data they were provided.

대다수는 기술적인 이슈였다. 

암튼 SDV라는 게 잘 됐다고 한다.

 

 

 

 

나의 생각:

 

암튼 2016년에 나온 생성 모델 관련해서 Trick을 보고자 한번 쭉 봤다.

일단 평가하는 방법 , Numeric은 잘 모르겠고~ , Categorical은 Numeric으로 대체한 점.

그리고 Missing에 대한 생각을 배울 수 있었다. 

일단 하고자 하는 방향에서 크게 벗어나지 않는 느낌이라서 잘하고 있는 것 같다!

 

https://dai.lids.mit.edu/wp-content/uploads/2018/03/SDV.pdf

불러오는 중입니다...