2024. 4. 13. 16:24ㆍ관심있는 주제/LLM
LLM 같은 거대 모델을 학습할 때는 학습 속도를 어떻게 빠르게 할지가 중요합니다.
하지만 학습을 하다 보면 필요한 리소스 역시 증가해서, 이러한 리소스를 줄이면서 학습하는 것에 대한 연구들이 진행되고 있습니다.
이번에는 실제로 이러한 방법을 많이 사용하는 것 같아서 어떻게 동작하는 지 알아보고자 내용을 정리하려고 합니다.
그중에서 나온 게 바로 더 낮은 정밀도를 사용하는 방법에 대한 것이 나왔습니다.
일단 기존에 우리가 NN 모델을 학습할 때는 전통적으로 IEEE 단정밀도 형식(FP32)을 사용했습니다.
여기서는 FP32를 다 쓰는 게 아니라 혼합된 정밀도(Mixed Precision)를 쓰면 더 효율적이라는 겁니다
즉 FP32 와 FP16을 같이 써서 극복하자입니다.

Sign : 부호 / Exponent : 지수 / Mantissa : 가수
메모리 요구량 감소:
FP16은 FP32의 절반인 16비트를 사용하여 메모리를 절약함으로써 더 큰 모델 훈련 또는 더 큰 미니배치로 훈련할 수 있게 해 줍니다.
훈련 또는 추론 시간 단축:
메모리 또는 산술 대역폭에 민감한 실행 시간을 줄입니다. 반 정밀도는 액세스 되는 바이트 수를 절반으로 줄여 메모리 제한 레이어에서 소요되는 시간을 줄입니다. NVIDIA GPU는 단정밀도 대비 최대 8배 더 많은 반 정밀도 산술 처리량을 제공하여 수학적 제한을 빠르게 해 줍니다.
그러면 그렇게 했을 때 시간 단축과 메모리는 줄겠지만 성능에는 영향을 주지 않을까 하는 의문이 생길 수 있습니다.

위의 그림에서 큰 LSTM 영어 언어 모델의 훈련 곡선은 이 글에서 설명된 혼합 정밀도 훈련 기술의 이점을 보여줍니다.
Y축은 훈련 손실입니다. 손실 스케일링 없는 혼합 정밀도(Mixed-Precision) (회색)는 어느 정도 시간이 지나면 발산하나,
손실 스케일링(loss scale)과 함께 사용하는 혼합 정밀도 (녹색)는 단일 정밀도 모델 (검은색)과 일치합니다.

NVIDIA글에서는 이 방법을 하기 위해서 3가지 기술을 사용했다고 합니다.
- accumulation of FP16 products into FP32
- loss scaling
- an FP32 master copy of weights
기술
Accumulation into FP32
NVIDIA Volta GPU 아키텍처는 Tensor Core 명령을 소개했습니다. 이 명령은 반 정밀도 행렬을 곱하고 결과를 단일 또는 반 정밀도 출력으로 누적합니다.
우리는 단일 정밀도로 누적하는 것이 좋은 훈련 결과를 얻는 데 중요하다는 것을 발견했습니다.
누적된 값은 메모리에 쓰기 전에 반 정밀도(FP16)로 변환됩니다.
cuDNN 및 CUBLAS 라이브러리는 산술을 위해 Tensor Core를 사용하는 다양한 기능을 제공합니다.
Loss Scaling
DNN을 훈련할 때 네 가지 유형의 텐서를 만납니다:
1. 활성화, 2. 활성화 그래디언트, 3. 가중치 및 4. 가중치 그래디언트입니다.
NVIDIA의 경험에 따르면 활성화, 가중치 및 가중치 그래디언트는 반 정밀도로 표현 가능한 값의 크기 범위 내에 있습니다. 그러나 일부 네트워크에서는 작은 크기의 활성화 그래디언트가 반 정밀도 범위 아래로 떨어집니다.
예를 들어, 아래 그림에 나타난 Multibox SSD 탐지 네트워크를 훈련할 때 발생하는 활성화 그래디언트의 히스토그램을 고려해 보겠습니다. 이 그림은 로그 2 스케일의 값 비율을 보여줍니다. 반 정밀도 형식에서 2^(-24) 보다 작은 값은 0이 됩니다
활성화 그래디언트는 대부분 작은 값으로, 일반적으로 1보다 작은 크기를 가집니다.
따라서 활성화 그래디언트를 FP16로 표현 가능한 범위로 "이동"시킬 수 있습니다.
SSD 네트워크의 경우, 그래디언트를 8배로 곱하는 것으로 충분했습니다.
이는 크기가 2^-(27) 보다 작은 활성화 그래디언트 값이 이 네트워크의 훈련에 관련이 없었음을 시사하며, [2^(-27), 2^(-24)) 범위의 값은 보존하는 것이 중요했습니다.

여기서 그러면 반 정밀도 표현 가능한 범위에 gradient가 들어가게 하기 위해서 loss scale 계수를 곱합니다.
단일 곱셉만 하면 연쇄 법칙에 의해서 스케일이 업이 되는 것을 보장합니다.
FP32 Master Copy of Weights
DNN 훈련의 각 반복(iteration)은 네트워크 가중치를 해당 가중치 그래디언트를 더하여 업데이트합니다.
가중치 그래디언트 크기는 특히 학습률과 곱셈 후 (또는 Adam 또는 Adagrad와 같은 옵티마이저에 대한 적응형으로 계산된 요소와) 해당 가중치보다 크게 작을 때가 많습니다.
이 크기 차이는 반 정밀도 표현에서 차이를 만들기에 너무 작으면 업데이트가 발생하지 않을 수 있습니다 (예: 큰 지수 차이로 인해 작은 가산이 이진 소수점을 정렬한 후 0이 됨).
이런 식으로 업데이트가 손실되는 네트워크의 간단한 해결책은 단일 정밀도로 가중치의 마스터 복사본을 유지 및 업데이트하는 것입니다. 각 반복에서 마스터 가중치의 반 정밀도 복사본이 만들어지고 전진 및 역전파에 모두 사용되어 성능 이점을 얻습니다. 가중치 업데이트 중에 계산된 가중치 그래디언트가 단일 정밀도로 변환되어 마스터 복사본을 업데이트하는 데 사용되며, 이 프로세스는 다음 반복에서 반복됩니다.
따라서 필요한 경우에만 반 정밀도 저장과 단일 정밀도 저장을 혼합합니다.
Mixed-Precision Training Iteration
위에서 소개한 세 가지 기술은 각 훈련 반복마다 다음 단계 순서로 결합될 수 있습니다.
전통적인 반복 절차에 추가된 부분은 굵게 표시되어 있습니다.

1. 가중치의 FP16 복사본 만들기
2. FP16 가중치 및 활성화를 사용하여 전방 전파하기
3. 결과 손실을 스케일 계수 S로 곱하기
4. FP16 가중치, 활성화 및 그래디언트를 사용하여 역방향 전파하기
5. 가중치 그래디언트를 1/S로 곱하기
6. 선택적으로 가중치 그래디언트 처리하기 (그래디언트 클리핑, 가중치 감쇠 등)
7. FP32의 마스터 가중치 업데이트하기
다양한 DNN 훈련 프레임워크의 스크립트에 혼합 정밀도 훈련 단계를 추가하는 예제는 혼합 정밀도 훈련 사용자 가이드에서 확인할 수 있습니다.
Pytorch Example (Video , Slide)
https://www.youtube.com/watch?v=9tpLJpqxdE8
https://docs.nvidia.com/deeplearning/performance/mixed-precision-training/index.html#manual_pytorch
Train With Mixed Precision - NVIDIA Docs
There are numerous benefits to using numerical formats with lower precision than 32-bit floating point. First, they require less memory, enabling the training and deployment of larger neural networks. Second, they require less memory bandwidth which speeds
docs.nvidia.com
mixed precision 방식으로 업데이트하는 방법 이해해 보기
왼쪽은 이런 방식으로 할 때 문제점이고 오른쪽은 그걸 어떻게 해결했는지에 대한 걸로 이해하면 좋을 것 같습니다.

FP32 Master Weights
부정확한 가중치 업데이트를 우선 방지하기 위해서 32비트로 모델 파라미터를 우선 저장해 두고,
Gradient Update 할 때는 FP16으로 하기 때문에 optimizer.zero_grad가 아닌 model.zero_grad로 하게 됩니다.
그다음에 업데이트되는 gradient를 master에 전달해 주는 작업을 중간에 하게 됩니다. ( model_grads_to_master_grads)
이제 2개의 싱크를 맞추기 위해서 master_params_to_model_params를 통해서 업데이트된 마스터 파라미터를 다시 FP16 파라미터에 복사하는 작업을 한다.





위의 작업만 그림으로 그리면 다음과 같습니다.

Loss (Gradient) Scaling
loss.backward()에서 fp16으로 할 때 위에서 말한 것처럼 문제가 발생할 수 있습니다.
바로 gradient가 너무 작을 때 반영할 수가 없게 된다는 것이 있습니다.
그래서 이 문제를 해결하기 위해서 loss scaling을 적용합니다.


그래서 아까 코드에서 다음과 같이 작은 값은 gradient를 방지하기 위해서 높여주는 작업을 하고, 실제로 master에서 업데이트하기 전에 다시 스케일을 줄이는 작업을 합니다.
그러면 기존에 우리가 알던 형태의 학습 방법이 나오게 됩니다.

Accumulate in FP32
FP16으로 하게 됐을 때, 기존에 사용하던 것보다 더 제한된 범위로 한정하기 때문에 일부 연산에서 여러 제한이 생겨서 NAN이 생길 수 있습니다.

그래서 그러한 문제를 해결하기 위해서 loss를 만들 때는 FP32를 사용합니다.


대략적인 구조를 이해했고, 또 여기서 궁금했던 것은 Scaling Factor는 보통 어떻게 정하는지가 궁금해졌습니다.
기존에 학습 코드를 보면 따로 설정하는 부분은 못 봤던 것 같습니다.
그래서 좀 더 찾아보니 NVIDIA에서 어떻게 설정하는지에 대한 내용적인 글이 있었습니다.
역전파 overflow는 계산된 가중치 그래디언트를 검사함으로써 쉽고 효율적으로 감지할 수 있습니다.
이전 섹션에서 가중치 그래디언트를 1/S로 곱하는 단계가 예시입니다.
일반적으로 상수이지만 통계를 기반으로 더 직접적인 선택이 가능하다고 합니다.
최대 절대 그래디언트 값과의 곱이 FP16에서 표현 가능한 최대 값인 65,504보다 작도록 값을 선택합니다.
기본 아이디어는 큰 스케일링 계수로 시작하고 각 훈련 반복에서 다시 고려하는 것입니다.
아래 예시를 하나 가져와 보면 이런 식으로 알아서 찾는 작업을 하는 것 습니다.
- FP32 형식의 가중치의 주요 복사본을 유지합니다.
- S를 큰 값으로 초기화합니다. (손실 스케일링 계수)
- 각 반복에서 다음을 수행합니다:
- 가중치의 FP16 복사본을 만듭니다.
- FP16 가중치와 활성화를 사용하여 전방 전파를 진행합니다.
- 결과 손실을 스케일링 계수 S로 곱합니다.
- FP16 가중치, 활성화 및 그래디언트를 사용하여 역전파를 진행합니다.
- 가중치 그래디언트에 Inf(무한대) 또는 NaN(Not a Number)이 있는 경우:
- S를 줄입니다.
- 가중치 업데이트를 건너뜁니다. 그리고 다음 반복으로 이동합니다.
- 가중치 그래디언트를 1/S로 곱합니다.
- 가중치 업데이트를 완료합니다(그래디언트 클리핑 등 포함).
- 최근 N번의 반복에서 Inf나 NaN이 발생하지 않았다면 S를 증가시킵니다.
(https://pytorch.org/docs/stable/amp.html)
# set the self.scalar for scaling the model's gradients
self.scalar = torch.cuda.amp.GradScaler(enabled=True)
for epoch in range(parser.epochs):
print(f"Training Epoch {epoch}")
for text, label in tqdm(self.train_dataloader):
self.optimizer.zero_grad()
loss, acc = self.process_batch(text, label)
"""
Scaling is applied to multiply model parameters' gradients with small magnitude by a scalar factor which prevents
gradients Underflow(a condition in which gradients with small magnitude vanish to zero)
"""
self.scalar.scale(loss).backward()
"""
We need to unscale the gradients before updating the model parameters to prevent the scaling factor
used in scaling from interferring with model's paramters like learning rate.
self.scalar.unscale_(optimizer) unscales the gradients
"""
self.scalar.unscale_(self.optimizer)
비교(속도, 성능)
- 더 빠른 학습
- 유사한 성
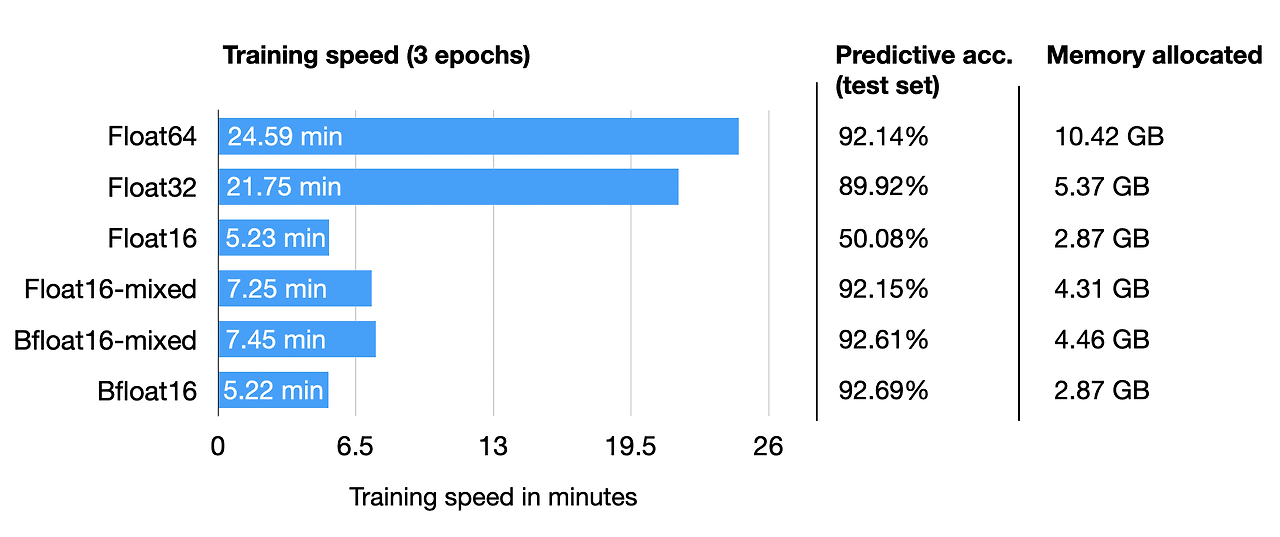
추론
- 더 적은 메모리
- 더 빠른 속도
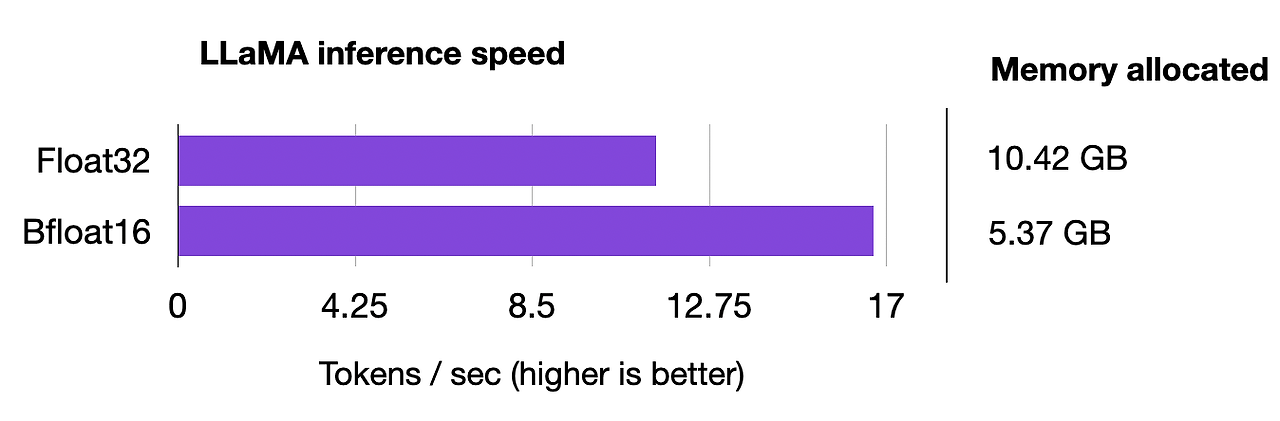
결론
mixed precision 사용 이유가 작동 방식에 대해서 알게 되었고, 이게 결국에는 어디 간에 가중치를 하나 더 복제해야 하니 램이나 디스크에 용량이 더 필요할 수 있겠다는 생각이 들고, 간혹 내가 몇 번 실패했을 때 ram이 왜 엄청 올라가는지에 대해서 이해하게 된 것 같습니다.
그리고 간혹 mixed precision 방식으로 학습을 시키다 보면 nan이 떠서 당황을 한 적이 있는데, 실제로 이러한 로직으로 scaling factor를 찾는 거라면 nan이 발생할 수도 있다는 것을 알게 된 것 같습니다.
그리고 여기서는 위에서 말한 nan 문제로 인해서 fp16 은 추론할 때 사용하고 bf16을 학습할 때 사용한다고 합니다.
참고
https://sebastianraschka.com/blog/2023/llm-mixed-precision-copy.html
Accelerating Large Language Models with Mixed-Precision Techniques
Training and using large language models (LLMs) is expensive due to their large compute requirements and memory footprints. This article will explore how lev...
sebastianraschka.com
https://blog.paperspace.com/mixed-precision-training-benchmark/
Benchmarking GPUs for Mixed Precision Training with Deep Learning
In this tutorial, we examine mixed-precision training to try and understand how we can leverage it in our code, how it fits into the traditional DL algorithmic paradigm, what frameworks support mixed precision training, and performance tips on using GPUs f
blog.paperspace.com
https://magazine.sebastianraschka.com/p/accelerating-pytorch-model-training
Accelerating PyTorch Model Training
Using Mixed-Precision and Fully Sharded Data Parallelism
magazine.sebastianraschka.com
Train and Deploy A Transformer Model-Mixed Precision Training and Deployment with ONNXRUNTIME
Step by step guide on training and deploying a transformer encoder network
olafenwaayoola.medium.com
https://arxiv.org/abs/1710.03740
Mixed Precision Training
Deep neural networks have enabled progress in a wide variety of applications. Growing the size of the neural network typically results in improved accuracy. As model sizes grow, the memory and compute requirements for training these models also increases.
arxiv.org
https://docs.nvidia.com/deeplearning/performance/mixed-precision-training/index.html
Train With Mixed Precision - NVIDIA Docs
There are numerous benefits to using numerical formats with lower precision than 32-bit floating point. First, they require less memory, enabling the training and deployment of larger neural networks. Second, they require less memory bandwidth which speeds
docs.nvidia.com
Accelerating Large Language Models with Mixed-Precision Techniques - Lightning AI
Training and using large language models (LLMs) is expensive due to their large compute requirements and memory footprints. This article will explore how leveraging lower-precision formats can enhance training and inference speeds up to 3x without compromi
lightning.ai
'관심있는 주제 > LLM' 카테고리의 다른 글
| LLM) 모델에서 사용하는 GPU 계산하는 방법 (0) | 2024.04.15 |
|---|---|
| LLM) Training 방법중 ORPO(Monolithic Preference Optimization without Reference Model) 알아보기 (0) | 2024.04.14 |
| LLM) PEFT 학습 방법론 알아보기 (1) | 2024.02.25 |
| LLM) Milvus 라는 Vector Database 알아보기 (0) | 2023.11.11 |
| LLM) BloombergGPT 논문 읽기 (1) | 2023.11.02 |