2023. 2. 21. 22:10ㆍML(머신러닝)
현재 다루고자 하는 데이터의 성격이 중도절단된 형태의 데이터이고, 생존 분석의 성격을 가지고 있는 것 같아, 내용들에 대해서 정리해보려고 한다.
생존 분석(Survival Analysis)은 관심 있는 사건이 발생할 때까지 예상되는 기간을 조사하는 데, 널리 사용되는 통계적 방법입니다.
| 의학 |
|
| 공학 |
|
| 경제 |
|
| HR |
|
성취자의 직원 참여 및 유지 보고서에 따르면 2021년에 새로운 일자리를 찾을 계획인 근로자의 52%와 31개국 3만 명 이상의 근로자가 참여한 최근 설문조사에 따르면 직원의 40%가 직장을 그만둘 생각을 하고 있는 것으로 나타났다고 합니다.. Forbes는 이러한 추세를 "Turnover Tunami"라고 부르는데, 이는 대부분 유행병의 소진에 의해 발생하며, Linkedin 전문가들은 big talent 인재들이 곧 이주를 도래할 것으로 예측하고 #Great Resignment 및 #Great Reshuffle 주제로 논의합니다.
항상 그렇듯이 데이터는 직원의 참여와 유지를 이해하여 이직률을 줄이고 보다 적극적이고 헌신적이며 만족스러운 팀을 구성하는 데 도움이 될 수 있습니다.
인사팀이 직원 이직률 데이터에서 파악할 수 있는 몇 가지 예는 다음과 같습니다:
- 머무르거나 떠나는 직원들의 특정한 특징은 무엇입니까?
- 직원 그룹 간에 감소율이 유사합니까?
- 직원들이 일정 시간이 지나면 퇴사할 확률이 얼마나 되나요? (즉, 2년 후)
데이터 선택
Kaggle에서 제공되는 IBM이 만든 가상의 직원 감소 및 성과 데이터 세트를 사용하여 직원 감소율과 중요한 직원 특성을 조사하여 현재 직원의 생존 기간을 예측할 것입니다.
생존함수 개념
이벤트(Event)는 생존/사망 또는 체류/사퇴와 같은 관심 경험입니다
생존 시간(Survival time)은 관심 있는 사건이 발생할 때까지의 기간입니다. 해당 데이터에서는 직원이 퇴사할 때까지의 기간입니다
Censorship Problem(절단 문제)
관측 중단 관측치(Censored observations)는 사건이 일부 개인에 대해 기록되지 않은 경우 사건 발생 시간 데이터에서 발생합니다. 이는 두 가지 주요 원인 때문일 수 있습니다
- 이벤트가 아직 발생하지 않은 경우(즉, 생존 시간을 알 수 없음/아직 사임하지 않은 사람의 경우 오해의 소지가 있음)
- 데이터가 누락되거나(즉, 드롭아웃) contact 하는 포인트를 잃게 된 것 경우
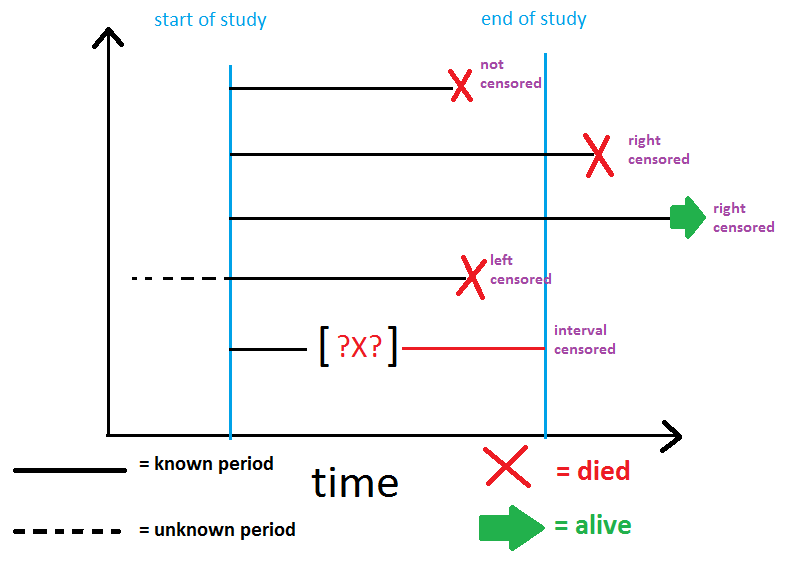
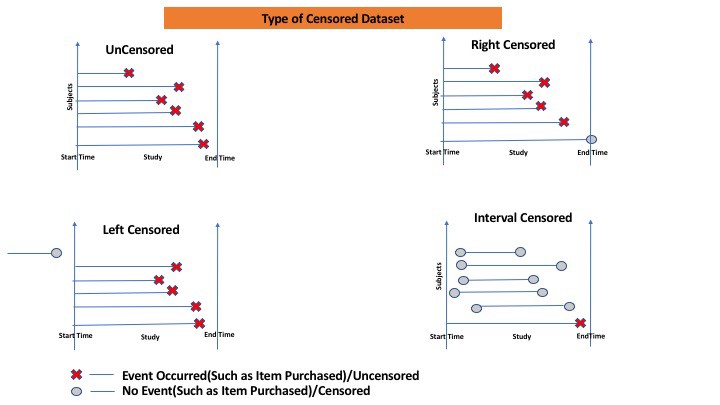
Censorship Problem Type
- 좌측 관측 중단(Left-Censored): 생존 기간이 관찰된 기간보다 작습니다
- 우측 관측 중단(Right-Censored): 생존 기간이 관찰된 기간보다 큽니다
- 구간 - 관측 중단됨(Interval-Censored): 생존 기간을 정확히 정의할 수 없습니다
가장 일반적인 유형은 우측 관측 중단(Right-Censored)이며 일반적으로 생존 분석을 통해 처리됩니다.
그러나 나머지 두 개는 데이터에 문제가 있음을 나타내며 추가 조사가 필요할 수 있습니다.
아래 그림과 같이 타입을 보면 이런 식으로 구성된다.
다른 그림으로는 다음과 같다.
Survival Function
T는 사건이 발생하고 t가 관측 중인 임의의 시점일 때 생존 S(t)는 T가 t보다 클 확률입니다.
즉, 생존 함수는 시간 t 이후에 개인이 생존할 확률입니다.
S(t) = Pr(T > t)
Survival Curve
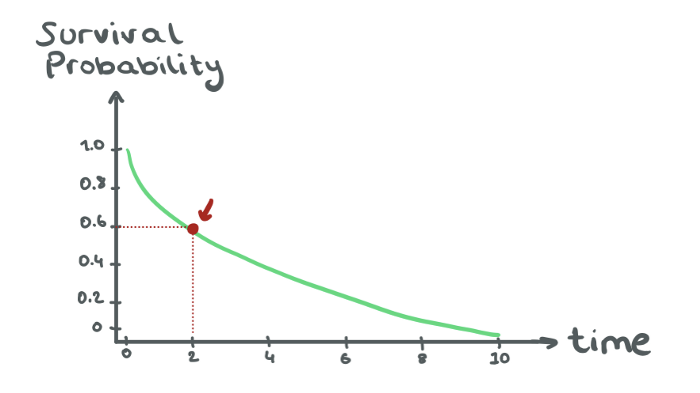
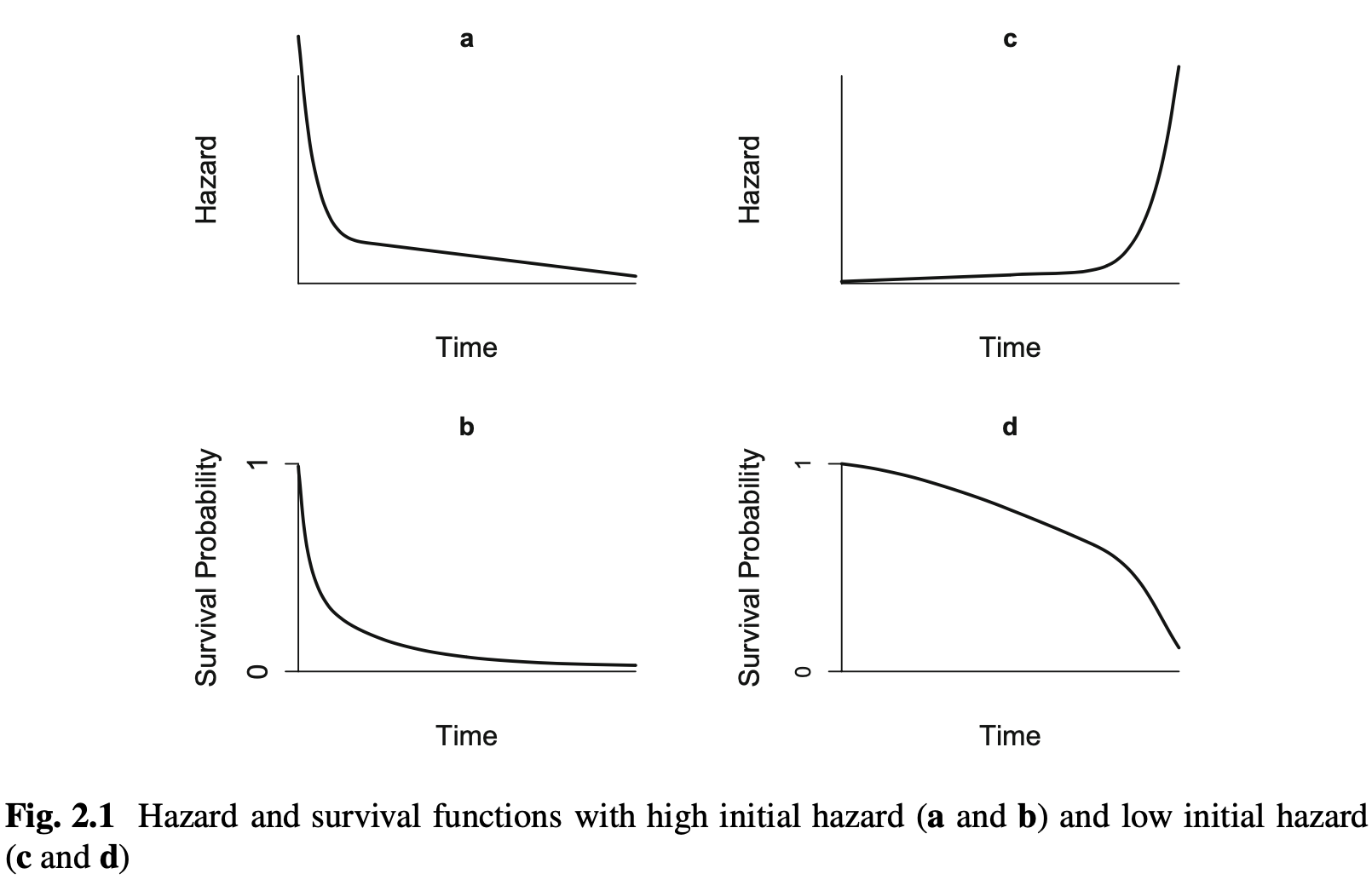
Survival Function characteristics
- T ≥ 0 and 0 < t < ∞
- It is non-increasing
- If t=0, then S(t)=1(survival probability is 1 at time 0)
- If t=∞, then S(t)=0(survival probability goes to 0 as time goes to infinity
Hazard Function
Hazard function는 위험함수라고 불린다.
위험 함수 또는 위험률 h(t)는 개인이 시간 t까지 생존하고 정확히 시간 t에 관심 있는 사건을 경험할 확률입니다.
위험 함수와 생존 함수는 다음 공식을 사용하여 서로 유도할 수 있습니다.
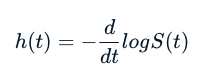

위험함수의 의미를 좀더 자세히 알아보자.
- 위험함수는 아주 짧은 시간에 일아날 사건의 확률로서 순간적인(instantaneous)인 의미를 가진다. 정의에서 보듯이 아주 짧은 시간에 일어나는 극한의 의미이다.
- 위험함수는 확률로서 정의되지만 발생률(rate)로 이해할 수 있다. 위험함수를 정의에서 분모는 확률이고 분자는 시간으로 표시되기 때문에 마차 단위 시간당 일어나는 발생률로 이해할 수 있다. 또한 위험함수의 값은 [0,1] 사이에 있는 것이 아니기 때문에 단위 시간당 발생률로 이해하는 것이 편리하다 (
- 위험함수는 조건부 확률로 정의되어 있다. 즉, 모든 개체에 대한 사건이 아니라 시간 까지 살아있는 개체들에 대한 위험율이다.
- 생존분석에서는 생존함수보다 위험함수가 더 큰 의미를 가진다. 위험함수가 시간에 따라서 변하는 추세는 시간에 따른 위험의 변화를 나타내기 때문에 생존함수보다 위험의 변화에 대한 정보를 잘 파악할 수 있다.

생존 분석 분석 방법론

Kaplan-Meier Estimator(Non-Parametic)
기존의 생존 함수 같은 경우, 특정 분포를 가정해야 위험 함수를 사용한다.
$f_t$ 에 대한 분포 가정이 필요하다는 것이 특징이다.
캐플런-마이어(Kaplan-Meier Estimator)는 비모수 추정 기이기 때문에 데이터 분포에 대한 초기 가정을 할 필요가 없습니다. 또한 관측된 생존 시간의 생존 확률을 계산하여 우측 관측 중단 관측치를 처리합니다. 확률의 곱 규칙을 사용하며, 실제로는 곱 한계 추정 기라고도 합니다.
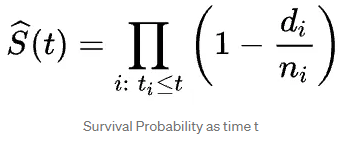
$d_i$ : 시간 $t_i$에서 발생한 이벤트 수입니다
$n_i$ : $t_i$까지 생존한 피험자 수입니다
시간 $t_i$에서의 생존 확률은 이전 시간 $t_{i-1}$에서의 생존 확률과 시간 $t_i$에서의 생존 확률의 백분율의 곱과 같다고 생각할 수 있습니다.

분석
Survival Function with KMF(KaplanMeierFitter)
일반적으로 생존 함수는 Kaplan-Meier Estimation 방법을 통해 추정할 수 있습니다.
해당 방법은 적은 표본에 대해서도 적용할 수 있기 때문에 폭넓게 사용됩니다.
Kaplan-Meier Estimation 방법을 통해 집단 간의 시간에 따른 생존율을 쉽게 비교할 수 있습니다.
Kaplan-Meier Estimation 방법은 전체 연구 기간 동안에 사건이 발생한 시점마다 구간생존율을 산출하여 최종적으로는 누적생존율을 산출합니다. 이 때문에 누적한 계추정법(Product Limit Method)으로 불리기도 하며, 사건이 발생한 시점마다 생존율을 계산합니다.
사건의 관찰기간 순서대로 자료를 정렬한 뒤, 각 구간별로 관찰대상 수 중 생존자수의 비율로 구간생존율 P(t)를 산출합니다.


예를 들어 위와 같은 데이터가 있을 경우
time 4인 경우를 가정해서 생각해 보면,
time=1일 때는 전원 생존하니까 10/10
time=2일 때도 전원 생존하고, time =1일 때도 전원 생존이니 1x1
time=3일 때도 전원 생존하고, time =2일 때도 전원 생존이니 1x1
즉, time=4일 때는 한 명 이벤트 발생하여, 9/10 x 1 = 0.9
위와 같이 비모수적 통계 방법으로 생존 분석을 수행할 수 있다.
아래는 좀 더 큰 데이터로 수행해 봤다
df[['YearsAtCompany','Attrition']].head()

# Convert the Attrition into binary variable
encoder = LabelEncoder()
df['Attrition'] = encoder.fit_transform(df['Attrition'])Attrition을 인코딩해주고 KMF를 적용한다.
from lifelines import KaplanMeierFitter
kmf = KaplanMeierFitter()
kmf.fit(durations=df['YearsAtCompany'], event_observed=df['Attrition'])
kmf.survival_function_.plot(figsize=(8,5))
plt.title('Survival Curve estimated with Kaplan-Meier Fitter')
plt.show()
kmf.plot_survival_function(figsize=(8,5))
plt.title('Survival Curve estimated with Kaplan-Meier Fitter with confidence intervals')
plt.show()
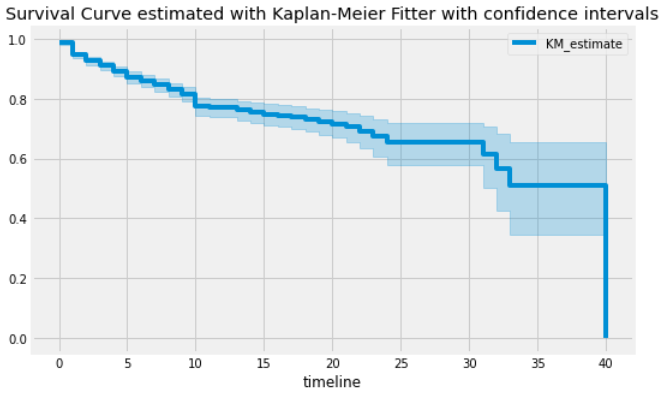
신뢰구간을 구하는 공식을 찾아보니 다음과 같다.


그리고 명확하게 그룹을 나눌 필요가 있다면, 나눠서 분석을 수행해야 한다.
예를 들어 아래 같은 경우 환경에 대한 만족에 따라서 생존 분석을 수행하고 싶으면 다음과 같이 수행할 수 있다.
EnvironmentalLow = ((df['EnvironmentSatisfaction'] == 1) | (df['EnvironmentSatisfaction'] == 2))
EnvironmentalHigh = ((df['EnvironmentSatisfaction'] == 3) | (df['EnvironmentSatisfaction'] == 4))
ax = plt.subplot()
kmf = KaplanMeierFitter()
kmf.fit(durations=df[EnvironmentalLow]['YearsAtCompany'],
event_observed=df[EnvironmentalLow]['Attrition'],
label='Low')
kmf.survival_function_.plot(figsize=(8,5), ax=ax)
kmf.fit(durations=df[EnvironmentalHigh]['YearsAtCompany'],
event_observed=df[EnvironmentalHigh]['Attrition'],
label='High')
kmf.survival_function_.plot(figsize=(8,5), ax=ax)
plt.title('Survival Function based on Environmental Satisfaction')
plt.show();신뢰구간 포함한 분석
EnvironmentalLow = ((df['EnvironmentSatisfaction'] == 1) | (df['EnvironmentSatisfaction'] == 2))
EnvironmentalHigh = ((df['EnvironmentSatisfaction'] == 3) | (df['EnvironmentSatisfaction'] == 4))
ax = plt.subplot()
kmf = KaplanMeierFitter()
kmf.fit(durations=df[EnvironmentalLow]['YearsAtCompany'],
event_observed=df[EnvironmentalLow]['Attrition'],
label='Low')
kmf.plot_survival_function(figsize=(8,5), ax=ax)
kmf.fit(durations=df[EnvironmentalHigh]['YearsAtCompany'],
event_observed=df[EnvironmentalHigh]['Attrition'],
label='High')
kmf.plot_survival_function(figsize=(8,5), ax=ax)
plt.title('Survival Function based on Environmental Satisfaction')
plt.show();

또한 예를 들어 아래 같은 경우 성별에 대한 만족에 따라서 생존 분석을 수행하고 싶으면 다음과 같이 수행할 수 있다.
male = (df['Gender'] == 'Male')
female = (df['Gender'] == 'Female')
ax = plt.subplot()
kmf = KaplanMeierFitter()
kmf.fit(durations=df[male]['YearsAtCompany'], event_observed=df[male]['Attrition'], label='Male')
kmf.survival_function_.plot(figsize=(8,5), ax=ax)
kmf.fit(durations=df[female]['YearsAtCompany'], event_observed=df[female]['Attrition'], label='Female')
kmf.survival_function_.plot(figsize=(8,5), ax=ax)
plt.title('Survival Function based on Gender')
plt.show();
worklifelow = ((df['WorkLifeBalance'] == 1) | (df['WorkLifeBalance'] == 2))
worklifehigh = ((df['WorkLifeBalance'] == 3) | (df['WorkLifeBalance'] == 4))
ax = plt.subplot()
kmf = KaplanMeierFitter()
kmf.fit(durations=df[worklifelow]['YearsAtCompany'],
event_observed=df[worklifelow]['Attrition'],
label='Low')
kmf.survival_function_.plot(figsize=(8,5), ax=ax)
kmf.fit(durations=df[worklifehigh]['YearsAtCompany'],
event_observed=df[worklifehigh]['Attrition'],
label='High')
kmf.survival_function_.plot(figsize=(8,5), ax=ax)
plt.title('Survival Function based on Work Life Balance')
plt.show();
즉 이런 방식을 통해서 자기가 원하는 그룹들 간에 생존분석을 수행할 수 있고,
수많은 변수들 중에서 실제로 이런 것을 찾기 위해서는 도메인 지식이 필요할 것으로 보인다.
Log Rank Test
로그 순위법은 두 군 차이에서 유의미한 차이가 있는가를 확인하기 위해 사용한다고 한다.
로그 순위법에서는 두 군을 합하여 전체 집단을 관찰 기간 순으로 배열하고, 절단된 항목을 지우고 사건(event)이 발생한 구간만을 남긴다.
각 그룹별로 통계적으로 유의미한 차이가 있는 지를 검정하는 작업을 통해 유의미성을 검증한다.
from lifelines.statistics import logrank_test
output = logrank_test(durations_A = df[worklifelow]['YearsAtCompany'],
durations_B = df[worklifehigh]['YearsAtCompany'],
event_observed_A = df[worklifelow]['Attrition'],
event_observed_B = df[worklifehigh]['Attrition'])
output.print_summary<bound method StatisticalResult.print_summary of <lifelines.StatisticalResult: logrank_test>
t_0 = -1
null_distribution = chi squared
degrees_of_freedom = 1
test_name = logrank_test
---
test_statistic p -log2(p)
4.40 0.04 4.80>전체 변수에 대해서 logrank test 수행해 보기
각 범주별로 비교했을 때 유의미한 차이가 있는 변수를 찾는 작업을 수행함
일부 패턴에서는 차이가 없지만, 대부분의 그룹 간에 차이가 있다는 식으로 나옴.
from lifelines.statistics import logrank_test
group_cols = ['BusinessTravel',
'Department',
'EducationField',
'Gender',
'JobRole',
'MaritalStatus',
'Over18',
'OverTime']
results = []
for col in group_cols :
choices = list(df[col].unique())
print(col,choices)
candidates = list(combinations(choices,2))
for a_group, b_group in candidates :
A_GROUP = df.query(f"{col}=='{a_group}'")
B_GROUP = df.query(f"{col}=='{b_group}'")
output = logrank_test(durations_A = A_GROUP['YearsAtCompany'],
durations_B = B_GROUP['YearsAtCompany'],
event_observed_A = A_GROUP['Attrition'],
event_observed_B = B_GROUP['Attrition'])
p_value = output.p_value
results.append([col,a_group,b_group,p_value])
result_table = pd.DataFrame(results,columns=['column',"a_group","b_group","p_value"])
result_table['p_value'].plot.hist()

ax = plt.subplot()
kmf = KaplanMeierFitter()
a_group = df['OverTime'] == 'Yes'
b_group = df['OverTime'] == 'No'
kmf.fit(durations=df[a_group]['YearsAtCompany'],
event_observed=df[a_group]['Attrition'],
label='OverTime==Yes')
kmf.survival_function_.plot(figsize=(8,5), ax=ax)
kmf.fit(durations=df[b_group]['YearsAtCompany'],
event_observed=df[b_group]['Attrition'],
label='OverTime==No')
kmf.survival_function_.plot(figsize=(8,5), ax=ax)
plt.title('Survival Function based on OverTime')
plt.show();
Cox Proportional-Hazards Model

Cox 비례위험 모형(Cox proportional hazard model)은 생존 기간과 영향을 미치는 여러 가지 요인들을 알아보는 분석 방법이다. 해당 모델은 hazrad assumption이 유지된다는 가정해야 할 수 있는 방법이다.
Cox-model과 똑같은 거라고 할 수 있지만, hazard assumption이 다르기 때문에 다르다고 할 ㅅ ㅜ있다.
앞서 소개한 Kaplan-Meier과 Log Rank Test는 Event의 발생 여부만을 고려하여, 분석을 수행하지만, Cox 분석은 생존에 영향을 미치는 여러 risk factor 즉 위험요소에 대한 분석을 한다.

가정
- 샘플간에 생존 시간은 독립적이다.
- 예측 변수와 hazard 사이에 곱셈 관계
- 시간이 지남에 따라 일정한 위험 비율
위험(Hazard)은 생존 곡선의 기울기로 정의됩니다. 피험자가 얼마나 빨리 죽어가는지를 측정한 것입니다.
위험 비율은 두 그룹을 비교합니다. 위험비가 2.0이면 한 그룹의 사망률은 다른 그룹의 사망률의 두 배입니다.
Why it's called "proportional"
왜 비례라는 표현이 있게 되냐면, 단위가 하나 증가할수록 계수의 지수배만큼 증가하는 효과가 있다.
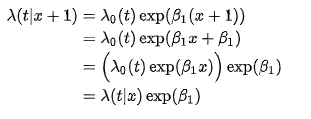

Code
# Prepare the dataframe for fitting
columns_selected = ['Attrition',
'EnvironmentSatisfaction',
'JobInvolvement',
'JobLevel',
'JobSatisfaction',
'PercentSalaryHike',
'RelationshipSatisfaction',
'StockOptionLevel',
'TrainingTimesLastYear',
'YearsAtCompany',
]
df = df[columns_selected]
from lifelines import CoxPHFitter
coxph = CoxPHFitter()
coxph.fit(df,
duration_col='YearsAtCompany',
event_col='Attrition')
# Current employees
df_new = df.loc[df['Attrition'] == 0]
# Years at the company of current employees
df_new_obs = df_new['YearsAtCompany']
# Predict survival function for the employes still in the company
predictions = coxph.predict_survival_function(df_new,
conditional_after=df_new_obs)
pd.DataFrame(predictions).head(11).iloc[:, :5]
5명에 대해서 향후 기간 동안의 생존 분석을 수행하면 다음과 같다.
pd.DataFrame(predictions).head().T.plot(figsize=(21,6))
변수 유의 수준
해당 계수를 보면 exponential이 쓰인 결과를 얻는 것을 알 수 있다.
콕스 회귀분석에서는 종속변수에 영향을 미치는 크기를 HR(Hazard Ratio)라고 한다.
그래서 실제 계수에 대한 값을 구하려면 log를 씌워야 한다.
해석을 할 때는 exp(coef)를 보고 해석을 하면 된다.
연속형 변수에 대한 값은 단위가 하나 증가할수록 exp(coef) 배로 위험 비율(HR)이 된다고 할 수 있다.
범주형 변수 같은 경우 특정 기준 변수 대비 exp(coef)배로 위험 비율(HR)이 된다고 할 수 있다.
아래에서는 관계에 대한 만족도나 연봉인상률? 에 따라서 이탈 여부가 결정된다고 모델 결과가 나왔다.
변수에 대해서만 봤을 때는 납득이 되는 결과라고 생각한다.
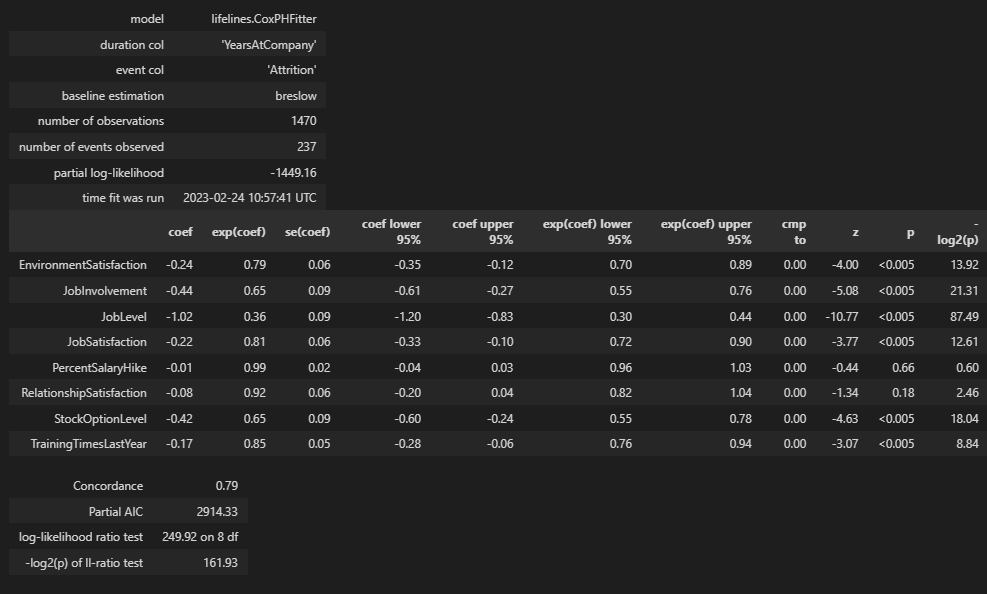
coxph.plot()

해당 데이터가 가정을 잘 만족하는지 확인할 수 있다.
coxph.check_assumptions(df)
# Proportional hazard assumption looks okay.
Accelerated Failure Time (AFT) Model
Cox-PH 모델의 비례 위험 가정 기준을 만족하지 못하는 경우에는 파라메트릭 모델을 사용하는 것이 더 나은 접근 방식이다. Accelerated Failure Time(AFT)은 생존 분석에 사용되는 인기 있는 파라메트릭 모델 중 하나이다.
이 모델은 생존 함수가 모수적 연속 분포를 따른다고 가정합니다.
예를 들어 Weibull 분포 또는 로그 정규 분포를 가정할 수 있습니다.
The parametric AFT model은 두 모집단(예: P 및 Q)에서 파생된 생존 함수가 공변량의 함수로 모델링할 수 있는 acceleration 계수 람다(λ)와 관련이 있다고 가정합니다.

공변량을 기반으로 AFT 모델은 고장 시간을 가속화하거나 감속할 수 있다.
AFT 모델 계수는 쉽게 해석할 수 있다고 한다
공변량의 단위 증가는 평균/중간 생존 시간이 exp(b_i)[2]의 인자만큼 변경됨을 의미한다
Identifying the Best Fitted Distribution
맞출 수 있는 분포가 많이 있다.
따라서 첫 번째 단계는 데이터에 가장 잘 맞는 최상의 분포를 식별하는 것이다.
일반적인 분포는 Weibull, Exponential, Log-Normal, Log-Logistic 및 Generalized Gamma이다
from lifelines import WeibullFitter,\
ExponentialFitter,\
LogNormalFitter,\
LogLogisticFitter
# Instantiate each fitter
wb = WeibullFitter()
ex = ExponentialFitter()
log = LogNormalFitter()
loglogis = LogLogisticFitter()
# Fit to data
for model in [wb, ex, log, loglogis]:
model.fit(durations = df["YearsAtCompany"].replace(0 , 0.000001), event_observed = df["Attrition"])
# Print AIC
print("The AIC value for", model.__class__.__name__, "is", model.AIC_)
The AIC value for WeibullFitter is 2138.2708129525727
The AIC value for ExponentialFitter is 2263.9437336059136
The AIC value for LogNormalFitter is 2276.8859677966007
The AIC value for LogLogisticFitter is 2151.5797690015165LogLogistic_aft = LogLogisticFitter()
LogLogistic_aft.fit(durations=df['YearsAtCompany'].replace(0 , 0.000001), event_observed=df['Attrition'])
LogLogistic_aft.print_summary(3)
LogLogistic_aft.survival_function_.plot(figsize=(8,5))
plt.show();
Interpretation of AFT Model Results/Estimates
계수가 양수이면 exp(계수)가 >1이 되어 사건/이벤트 시간이 느려집니다. 마찬가지로 음의 계수는 평균/중간 생존 시간을 줄입니다.
print(LogLogistic_aft.median_survival_time_)
# 123.01280287855722plt.subplots(figsize=(10, 6))
LogLogistic_aft.plot()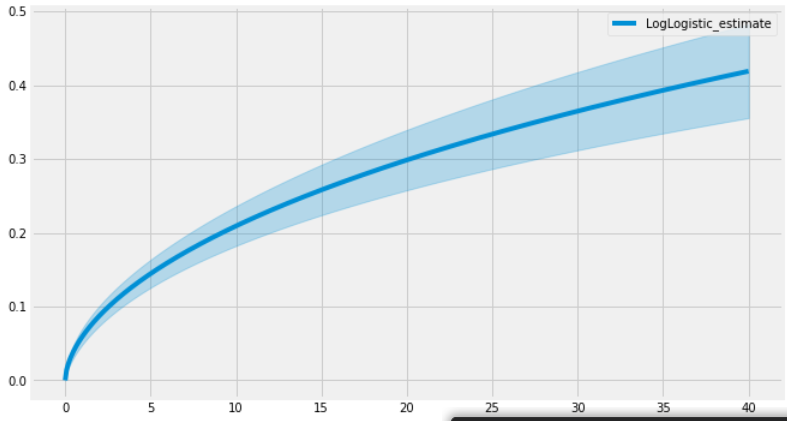
참고
GitHub - Idilismiguzel/Machine-Learning
Contribute to Idilismiguzel/Machine-Learning development by creating an account on GitHub.
github.com
https://towardsdatascience.com/hands-on-survival-analysis-with-python-270fa1e6fb41
https://ilovedata.github.io/teaching/biostat-grad/survival/survivalintro.html
https://www.kaggle.com/datasets/pavansubhasht/ibm-hr-analytics-attrition-dataset
Confidence Interval Survival Function | Real Statistics Using Excel
We now show how to estimate the standard error and confidence intervals for the estimated survival function at any time t based on the Kaplan-Meier procedure. Property 1 (Greenwood): The standard error of S(t) for any time t, tk ≤ t < tk+1 is approxim
real-statistics.com
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=euleekwon&logNo=221441257643
[통계 공부] Log-rank test(로그 순위법)
로그 순위법은 두 군 차이에서 유의미한 차이가 있는가를 확인하기 위해 사용한다. 로그 순위법에서는 두 ...
m.blog.naver.com
'ML(머신러닝)' 카테고리의 다른 글
| Transformer 간단하게 코드와 함께 살펴보기 (1) | 2023.06.09 |
|---|---|
| Python) AutoML 라이브러리 정리 (0) | 2023.02.08 |
| [ML] 앙상블 모델 테크닉 (0) | 2022.07.16 |
| [Python] pycaret 패키지 (0) | 2020.08.30 |