목차
Why Kalman filters?
자율 주행 자동차를 만들고 환경에서 그 위치를 파악하려고 한다고 상상해 보면, 자동차의 센서는 자동차, 보행자, 자전거 이용자를 감지할 수 있습니다. 이러한 물체의 위치를 알면 차량이 판단을 내리고 충돌을 방지하는 데 도움이 됩니다. 그러나 자동차는 물체의 위치를 아는 것 외에도 미래의 위치를 예측해야 사전에 무엇을 할지 계획할 수 있습니다.
예를 들어, 도로를 향해 달리는 어린이를 감지하는 경우 어린이가 멈추지 않을 것으로 예상해야 합니다.
Kalman Filter는 시스템 상태의 추적 및 추정을 지원하는 데 사용되므로 이 문제를 해결하는 데 도움이 될 수 있습니다.
자동차에는 물체의 위치를 결정하는 센서와 물체의 미래 위치를 예측하는 모델이 있습니다. 그러나 현실 세계에서 예측 모델과 센서는 완벽하지 않습니다. 여기에 항상 약간의 불확실성이 있습니다. 예를 들어 날씨는 들어오는 감각 데이터에 영향을 줄 수 있으므로 자동차가 정보를 완전히 신뢰할 수 없습니다.
칼만 필터를 사용하면 우리가 가지고 있는 정보를 더 확신하는 분포와 결합하여 불확실성을 완화할 수 있습니다.
다른 분이 요약해서 정리한 것은 다음과 같다. https://pasus.tistory.com/104
칼만필터로 신호에 섞인 노이즈를 제거할 수 있다.
칼만필터로 센서가 측정하지 못하는 것도 추정할 수 있다.
칼만필터로 여러 센서를 융합하여 더 좋은 측정값을 만들 수 있다.
칼만필터로 기계 장치에 난 고장을 감지할 수 있다.
칼만필터로 적 항공기를 추적할 수 있다.
칼만필터로 선물 또는 주식의 가격을 예측할 수 있다.
필터란 말은 불순물을 걸러내는 물리적인 장치를 의미하며, 1930~40년대에는 필터의 개념이 확장되어서, 노이즈로부터 신호를 분리한다는 개념으로 사용되었다고 한다.
신호를 분리한다는 것은 노이즈와 신호의 합으로부터 신호를 추정한다는 뜻이었다.
선형 칼만 필터를 사용하고 위해서는 2가지 가정이 갖춰지는 경우에 사용할 수 있다.
- 모션 모델과 측정 모델이 선형(linear)인 경우
- 모션 모델과 측정 모델이 가우시안(Gaussian) 분포를 따를 경우
예로 다음과 같다.
- 모션 모델이란 로봇이 현재 위치에서 모션 입력을 입력받아서 움직였을 때의 확률 모델을 말함.
- 측정 모델은 로봇이 현재 위치에서 자신이 가진 센서를 이용해서 자신이 어디에 위치해 있는지를 측정했을 때의 확률 모델
http://jinyongjeong.github.io/2017/02/14/lec02_motion_observation_model/
간략히 말하면, 모션 모델은 이전 상태와 콘트롤 변수를 통해서 다음 상태로 변화시킬 사후 확률을 계산하는 모델을 의미하고, 크게 2가지 모델이 있다고 한다. odometry-based model velocity-based model 이 있다고 한다.
odometry model은 센서 데이터를 이용한 모델이며, velocity model은 odometry model을 사용할 수 없는 경우에 사용한다고 한다.
측정 모델(observation model)은 현재 state에서 센서 데이터의 확률을 의미한다고 한다. 현재 state 에서의 각 센서 데이터들의 확률의 곱으로 표현된다고 한다.
칼만 필터는 상태 예측(state prediction)과 측정 업데이트(measurement update)를 반복적으로 수행하며, 현재 위치를 계산한다.
- 상태 예측단계는 이전 로봇의 파라미터(위치, 속도 등)와 로봇 모션 입력을 이용해 현재 로봇 파라미터 값을 예측하는 단계
- 측정 업데이트는 상태 예측단계에서 예측된 현재 로봇의 파라미터 값과 현재 로봇의 위치에서 얻어진 센서 정보를 이용해 현재 로봇 파라미터 값을 업데이트하는 단계입니다.
Examining Errors
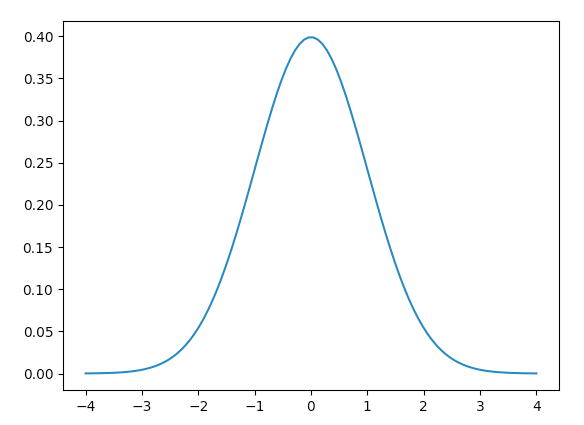
칼만 필터를 사용하면 추적하려는 변수의 예측과 측정 모두에 약간의 오류와 노이즈가 내재되어 있음을 인정하고 진행됩니다. 필터는 모든 오류가 가우시안이라고 가정하지 않지만 Wikipedia 설명에서 인용한 것처럼 "필터는 모든 오류가 가우스인 특별한 경우에 정확한 조건부 확률 추정치를 산출합니다." 가우시안은 평균(mu)과 가우시안의 너비, 즉 분산(시그마 제곱)의 두 가지 매개변수로 특징지어집니다.

분포를 히스토그램으로 나타내는 대신 Kalman 필터의 작업은 $\mu$ 및 $\signam^2$ 을 찾으려는 객체의 위치에 대한 최상의 추정치로 유지하는 것입니다.
Filter란?
측정 데이터가 포함된 불확실성을 필터하는 것으로, 측정 데이터나 신호가 잡음을 동반하는데, 여기서 원하는 신호나 정보를 골라내는 것이라고 볼 수 있음.
위의 공식에서 정규화 상수를 c로 요약했습니다. 왜냐하면 가장 중요한 것은 평균과 분산 사이의 관계를 알아보는 것이기 때문입니다.
Kalman 필터는 가우시안으로써 모든 분포를 나타내며 mearument updates나 motion updates라는 두 가지 다른 항목에 걸쳐 반복됩니다. mearument updates는 특정 belief의 산출물로써, 이전 업데이트를 포함하며 motion updates는 컨볼루션 수행을 포함합니다.
Measure Update
Measure Update는 베이즈 룰(Bayes Rule)을 따른다고 합니다.
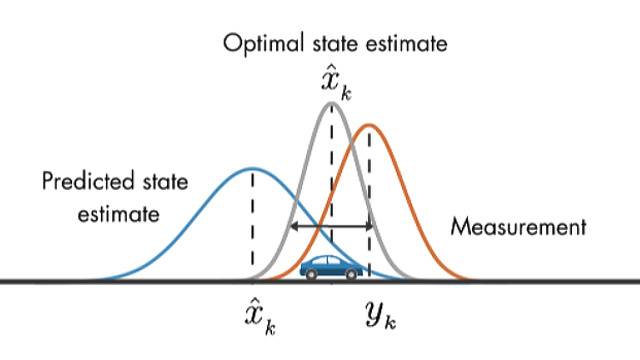
다른 차량을 지역화하여 편차가 매우 큰 사전 분포를 가정해 보십시오(큰 불확실성).
다른 측정 결과를 통해 해당 차량에 대한 편차가 더 작다는 것을 알 수 있습니다.
정보를 결합하여 새로운 가우스를 생성하면 평균은 이전 분포보다 피크가 높고 분산이 좁은 두 분포 사이의 어딘가에 있게 된다.
기존의 가우시안보다 합쳐지고 나서의 가우시안의 피크가 높다는 것(분산이 줄어듬)이 놀랍긴 하지만, 직관적으로 이치에는 맞습니다. 2개를 조합하면, 독립된 분포보다는 더 많은 정보를 얻을 수 있기 때문입니다.
다음 방정식에서 $\mu$ 및 $r^2$은 각각 새로 관찰된 데이터의 평균과 분산입니다.
이를 사용하여 이전 평균과 분산을 업데이트할 수 있습니다.
베이즈 룰에 따라서 사후 확률을 구하는 것을 의미합니다.
사전 확률과 우도 함수가 가우시안일 경우 사후 확률은 다시 가우시안이 되고, 그것에 대한 새로운 평균과 분산을 구한 것입니다.
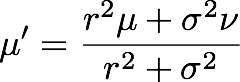

def updated_mean(mean1, var1, mean2, var2):
new_mean = (mean1 * var2 + mean2 * var1) / (var1 + var2)
return new_mean
def updated_var(var1, var2):
new_var = 1 / ((1 / var1) + (1 / var2))
return new_var
Prediction / Motion Update
사전에 그 차는 어떤 위치에서 시작되는 것으로 믿고 가정하지만, 움직이면, 위치가 이동하게 됩니다.
모션 자체는 가우스 분포와 불확실성을 가지고 있습니다. 우리는 평균에 모션 명령을 추가하고 초기 불확실성에 대한 불확실성을 증가시키는 예측에 도달한다.
우리는 위치를 바꿀수록 더 많은 불확실성을 축적합니다.


def predict(mean1, var1, mean2, var2):
new_mean = mean1 + mean2
new_var = var1 + var2
return [new_mean, new_var]
Designing a Kalman Filter
칼만 필터는 단일 모드(uni-modal), 재귀(recursive) 추정기입니다.
현재 상태를 예측하려면 이전 시간 단계 및 현재 측정에서 추정된 상태만 필요합니다.
아래의 흐름도는 재귀 프로세스를 보여줍니다. 처음부터 필터는 추적 중인 측정의 현재 값(예: 위치, 속도)을 포함하는 상태 변수를 추적하는 반면 프로세스 변수에는 해당 측정의 예측 오류가 포함됩니다.
각 시간 단계에서 상태 전이 행렬은 현재 위치와 속도를 기반으로 상태 및 프로세스 행렬을 이동하여 새로운 위치/속도 및 새로운 공분산을 추정합니다
여기서 Kalman Gain은 관측된 데이터와 함께 계산됩니다.
업데이트 프로세스에는 Kalman을 이전 추정치 및 새로운 관측 데이터와 결합하여 예측과 측정 사이에 있는 믿음에 대한 상태 변수를 업데이트하는 작업이 포함됩니다.
process 공분산도 Kalman Gain에 따라 업데이트됩니다. 그런 다음 이러한 업데이트는 다음 예측 라운드에 사용됩니다.

Kalman Gain
Kalman Gain은 새 추정치를 업데이트하는 데 사용할 새 측정값의 양을 결정하는 데 사용됩니다.
Kalman Gain을 계산하기 위해서는 두 가지가 필요합니다.
첫째, 추정치에 오류(error in the estimate)가 있어야 합니다. 추정치의 오류를 계산할 때마다, 우리는 그 정보를 칼만 이득을 갱신하기 위해 사용한다.
둘째, 데이터/측정에 오류(error in the data/measurement)가 필요합니다. 지속적으로 데이터 입력을 추정치로 가져오면 이득에 어떤 영향을 미치는지 결정해야 하기 때문입니다.
Gain은 추정치의 오류(errir in the estimate)와 측정의 오류(error in the measurmemnt) 사이에 상대적 중요성을 부여합니다. 추정치의 오차가 작으면 우리는 그것을 더 강조한다. 데이터 오류의 경우 그 반대입니다.
전체적인 계산을 제공하는 것은 예측과 데이터(오차에 근거하는 데이터)를 얼마나 신뢰할 수 있느냐에 따라 달라집니다.
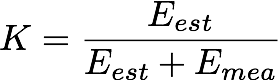
Kalman Gain의 값은 0과 1 어딘가에 있을 것입니다.
Kalman Gain은 현재 추정치의 값을 업데이트하는 데 사용됩니다.
아래 방정식에서 x는 추정치를 나타내고, K는 칼만 이득으로 측정치(p)와 이전 추정치 간의 차이를 곱합니다.
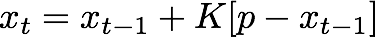
Kalman Gain이 1에 가까우면 측정값은 정확하지만 추정치는 불안정하다는 의미입니다.
측정의 오차가 작으면(그리고 $E_{st}$에 대한 $E_{est}$에 실질적으로 기여하지 않음), K는 1과 같아지는 Kalam Gain 비율을 살펴봄으로써 이를 추론할 수 있다.
측정 오차가 작을 경우 향후 예측은 새로운 입력 데이터를 기반으로 강력하게 업데이트된다.
그러나 Kalman Gain이 작으면 추정치의 오차가 추정치의 오차에 비해 큰 것입니다.
추정치가 더 안정적이고 측정값이 부정확합니다. 결과적으로, 새로운 데이터와 예측 사이의 차이는 최종 업데이트에 더 작은 영향을 미칩니다.
각 반복을 사용하면 모형에서 추정치가 실제 값에 더 가까워져 Kalman Gain이 더 작아집니다. 새로운 데이터는 불확실성이 클 수 있으므로 예측 모델에서 벗어나고 싶지 않게 됩니다.

아래 식처럼 추정치의 오차를 다시 계산하려면 측정 오차에 이전 추정치의 오차를 곱하고 오차의 합으로 나누기만 하면 됩니다.

여기서 E는 추정치의 오차이며 Kalman Gain에 이전 추정치 오차를 곱한니다. 이전 오차에 (1 - K) x$E_{t-1}$은 Kalman Gain 크기의 역수입니다.
Kalman Gain이 크면 측정의 오차가 작으므로 새 데이터가 모형을 참 값으로 빠르게 업데이트하여 결과적으로 추정치의 오차를 줄일 수 있습니다.
그러나 Kalman Gain이 매우 작으면 측정 오류가 매우 커야 하며 업데이트는 천천히 이루어져야 합니다.
즉 Kalman Gain은 궁극적으로 추정 값이 참값으로 영점화되는 속도를 촉진합니다.
State Matrix
상태 행렬은 추적 중인 개체를 기록합니다. 그것은 도로 위의 다른 자동차일 수도 있고 공중에 떠 있는 비행기일 수도 있습니다.

상태의 조건은 상태의 이전 조건과 제어 변수 행렬 $u_t$를 기반으로 업데이트되며 $w_t$는 프로세스를 통해 축적되었을 수 있는 노이즈를 나타냅니다.

상태 행렬에는 객체의 위치(x 및 y) 및 속도(x dot 및 y dot)와 같은 정보가 포함될 수 있습니다.


Matrix A x X는 다음 타임 스텝 (delta t)를 기반으로 현재 상태와 속도를 표현합니다. time step이 수행되면,, 속도는 물체의 위치를 업데이트하기 위해서 이전 위치에 속도가 추가됩니다.
속도는 동일하게 유지 것이고, 가속도로 인해 시간이 흐름에 따라서 변할지 모릅니다.(control variable matrix)
만약 가속이 있다면, 가속도가 속도에 영향을 받기 때문에 이러한 계산은 완전하지 않을 것입니다.
이 업데이트는 Matrix B x u에 적용됩니다.
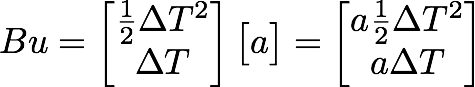
Matrix B는 속도와 가속도를 시간에 의해서 곱한 kinematics equation의 파트 일부를 모방합니다.
Matrix B는 control variable에 의해 곱해지고 그리고 AX를 더하면 가속으로 인해 위치와 속도가 변경됩니다.
Observation Data
칼만 필터 프로세스의 일부는 가장 최근의 예측을 포함하는 상태 행렬로 관찰 데이터를 전달합니다.
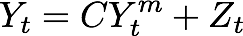
Observation은 Matrix C x variables observed(관측된 변수) + measurement nosie로 이루어집니다.
matrix C의 모양과 항목들은 우리가 관찰하고자 하는 변수들의 수에 의존합니다.
만약 우리가 Y에서 모든 변수를 조사하고 싶다면, C는 대체로 단위행렬이 될 것입니다.
만약 몇 개의 변수만 관측한다면, C는 Y 변수 일부를 버리는 방식으로 형성될 수 있습니다.
예를 들어, 들어오는 데이터가 4가지 항목(X, Y, X 속도, y 속도)을 포함하지만, 우리는 오로지 2개(x, y)만 사용하면, C는
유지하려는 정보만 제공하도록 구성될 수 있습니다( 이 경우 대각선을 따라 1이 있는 4 x 2 행렬).
Z는 measurement noise를 표현합니다.
State Covariance and Measurement Covariance Matrix
state covariance matrix는 추정치의 오차다. state matrices는 다음 states의 추청치들이다.
추정치에 잡음, 오차 및 불확실성 Q가 있으므로 공정 잡음 공분산 행렬이 추가되어 상태 공분산 행렬이 조정됩니다.
Kalman Gain이 예측 값 또는 측정된 값에 중점을 두는 데 사용됩니다.
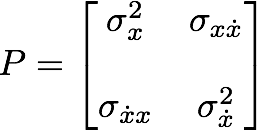
분산이 0으로 설정되면 해당 측정에서 상당히 큰 확신이 있음을 의미합니다.
따라서 예를 들어 x 위치의 상태 공분산이 0이면, x 위치 예측에 대한 높은 신뢰도를 의미합니다.
측정 공분산 행렬(R)은 측정의 오차입니다. 추적 중인 물체에 대해 측정을 수행할 때마다 측정값이 정확하다는 의미는 아닙니다. 추적하는 방식에 오류가 있을 수 있기 때문입니다.

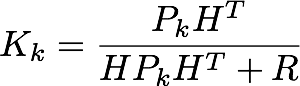
앞에서 말한 것을 상기해보자면, 측정 오류가 예측 오류에 비해 작을 경우 더 많은 신뢰를 주고자 합니다(따라서 Kalman Gain은 1에 가깝습니다). 그렇지 않으면 측정 오차가 예측 오차보다 크면 Kalman Gain은 예측과 측정 간의 차이를 덜 강조합니다.
P가 0이면 측정 업데이트가 무시됩니다. 이는 예측 값이 상당히 정확하고 관측치를 무시한다는 것을 의미합니다.
모형이 그러한 정확성을 가질 가능성은 매우 낮기 때문에 Q의 이점 중 하나는 P가 0이 되는 것을 막는 것이다.
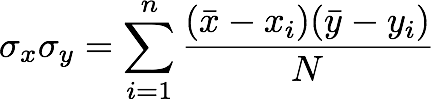
A 및 H 행렬은 주로 행렬 형식을 지정하는 데 도움이 됩니다.
Covariance는 2개의 랜덤 변수의 선형 관계를 나타내는 것을 의미한다.
만약 2개의 변수들 간의 동일한 행동을 보인다면, 양의 관계를 가지고, 반대의 의미를 가지면 음의 관계를 가진다.
이러한 신호는 2개의 변수들 간의 선형 관계의 의존성을 표현하기 때문에 중요하다.
다음은 x와 y의 분산이 주 대각선을 따라 있고 공분산이 대각선의 위쪽과 아래쪽 절반을 차지하는 단순 2x2 공분산 행렬입니다. x의 분산은 속도의 분산을 나타낼 수 있고 y는 위치의 분산을 나타낼 수 있습니다.

분산(더하기 및 빼기)은 분포 내에서 가능한 범위를 제공합니다. 또한 측정값을 예상할 수 있는 평균에서 얼마나 멀리 떨어져 있는지 알려주며, 어떤 값도 평균 마이너스/분산 범위를 벗어나지 않음을 거의 보장합니다.
ones 행렬과 A 행렬 사이의 dot product는 각 열에 각 과목에 대해 누적된 모든 마크의 합계를 포함하는 5 x 3 행렬을 생성하며, 각 과목에 대한 총 시험 횟수로 나누어 기본적으로 각 과목의 평균 등급을 제공한다. 그런 다음 A 행렬에서 평균을 빼서 편차를 생성합니다.
import numpy as np
A = np.array([[90, 80, 40],
[90, 60, 80],
[60, 50, 70],
[30, 40, 70],
[30, 20, 90]])
ones = np.ones([5, 5])
deviation = A - (ones.dot(A) / len(A))
covariance = deviation.T.dot(deviation)
import numpy as np
# Initial Values
x = 50
x_dot = 5
# Standard Deviations
x_std = 0.5
x_dot_std = 0.2
# Variance
x_var = x_std ** 2
x_dot_var = x_dot_std ** 2
x_cov_x_dot = x_std * x_dot_std
x_dot_cov_x = x_dot_std * x_std
X = np.array([[x], [x_dot]])
P = np.array([[x_var, x_cov_x_dot],
[x_dot_cov_x, x_dot_var]])
diagonal 부분이 0이라면, 추정 오차가 2개의 변수들간의 영향력이 없어서 독립이라고 할 수 있다.
이 경우 다른 변수의 추정 오차로 인해 한 변수의 추정치가 조정되지 않습니다. 이 값을 상태 업데이트 및 Kalman Gain과 같은 다른 행렬과 곱하면 공분산이 공정에 영향을 미치지 않습니다.
Putting it all together by tracking an aircraft with a Kalman Filter
import numpy as np
from numpy.linalg import inv
x_observations = np.array([4000, 4260, 4550, 4860, 5110])
v_observations = np.array([280, 282, 285, 286, 290])
z = np.c_[x_observations, v_observations]
# Initial Conditions
a = 2 # Acceleration
v = 280
t = 1 # Difference in time
# Process / Estimation Errors
error_est_x = 20
error_est_v = 5
# Observation Errors
error_obs_x = 25 # Uncertainty in the measurement
error_obs_v = 6
def prediction2d(x, v, t, a):
A = np.array([[1, t],
[0, 1]])
X = np.array([[x],
[v]])
B = np.array([[0.5 * t ** 2],
[t]])
X_prime = A.dot(X) + B.dot(a)
return X_prime
def covariance2d(sigma1, sigma2):
cov1_2 = sigma1 * sigma2
cov2_1 = sigma2 * sigma1
cov_matrix = np.array([[sigma1 ** 2, cov1_2],
[cov2_1, sigma2 ** 2]])
return np.diag(np.diag(cov_matrix))
# Initial Estimation Covariance Matrix
P = covariance2d(error_est_x, error_est_v)
A = np.array([[1, t],
[0, 1]])
# Initial State Matrix
X = np.array([[z[0][0]],
[v]])
n = len(z[0])
for data in z[1:]:
X = prediction2d(X[0][0], X[1][0], t, a)
# To simplify the problem, professor
# set off-diagonal terms to 0.
P = np.diag(np.diag(A.dot(P).dot(A.T)))
# Calculating the Kalman Gain
H = np.identity(n)
R = covariance2d(error_obs_x, error_obs_v)
S = H.dot(P).dot(H.T) + R
K = P.dot(H).dot(inv(S))
# Reshape the new data into the measurement space.
Y = H.dot(data).reshape(n, -1)
# Update the State Matrix
# Combination of the predicted state, measured values, covariance matrix and Kalman Gain
X = X + K.dot(Y - H.dot(X))
# Update Process Covariance Matrix
P = (np.identity(len(K)) - K.dot(H)).dot(P)
print("Kalman Filter State Matrix:\n", X)
state 행렬을 초기화하고, 추정에 특정한 x 위치와 x 속도의 분산에 해당하는 오류 항을 사용하여 추정 공분산 행렬로 P를 초기화했습니다.
그런 다음 제공된 각 관찰에 대해 일련의 프로세스를 반복하여 Kalman 필터에서 제공한 값으로 상태 행렬을 업데이트합니다.
먼저, 다음 단계에서 비행기가 어디에 있을지를 예측한다.
이 예측은 속도를 조정하는 가속도 매개 변수를 사용하여 이전 위치와 속도를 기반으로 합니다.
예측 2d 함수의 A 행렬은 경과된 시간을 기준으로 이전 상태를 업데이트합니다.
B 행렬은 가속도를 위치와 속도에 대한 조정으로 변환합니다. 공식 1/2 시간 제곱은 주어진 가속도를 찾는 데 사용됩니다.
그런 다음 공정/공분산 추정 행렬을 다음 시간 단계로 업데이트하여 미래를 예측했습니다.
이 연산은 행렬에 시간 단계를 추가한 다음 거리 오차의 분산을 업데이트합니다.
A 행렬은 상태 행렬 값을 예측하는 데 사용되는 행렬과 유사합니다. 비젠 교수가 대각선을 벗어난 값들을 없앴기 때문에, 나도 똑같이 했다.
Kalman Gain 계산에는 관측 오차에 대한 공분산 행렬을 계산하고 이를 사용하여 공정 공분산 행렬과 비교하는 작업이 포함됩니다.
이러한 문제의 경우, 필요한 것보다 더 많은 matrix rotation이 있을 수 있지만, 저는 이것이 공식을 다른 행렬 크기에 불변하게 만들기 위한 것이라고 생각합니다. 행렬 연산에는 나눗셈이 없습니다. 그래서 비율을 찾기 위해 저는 분모의 역수를 가진 dot product을 사용했습니다.
행렬 형식에서 Kalman Gain은 입력과 동일한 차원의 행렬이며, 대각선을 따라 관측된 위치와 속도를 조정하는 가중치가 있습니다. 가중치가 낮을수록 예측에 비해 모형이 관측치를 신뢰하는 값이 낮아집니다.
새로 계산된 Kalman Gain을 사용하여 관측 데이터와 예측 간의 차이를 측정한 다음 상태 행렬을 업데이트하는 데 사용했습니다. 또한 프로세스 공분산 행렬을 업데이트하기 위해 Kalman Gain을 사용했습니다.
Reference
https://medium.com/@jaems33/understanding-kalman-filters-with-python-2310e87b8f48
Understanding Kalman Filters with Python
Today, I finished a chapter from Udacity’s Artificial Intelligence for Robotics. One of the topics covered was the Kalman Filter, an…
medium.com
https://towardsdatascience.com/kalman-filtering-a-simple-introduction-df9a84307add
Kalman Filtering: A Simple Introduction
The optimal online learning algorithm for linear systems with Gaussian noise
towardsdatascience.com
https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python
GitHub - rlabbe/Kalman-and-Bayesian-Filters-in-Python: Kalman Filter book using Jupyter Notebook. Focuses on building intuition
Kalman Filter book using Jupyter Notebook. Focuses on building intuition and experience, not formal proofs. Includes Kalman filters,extended Kalman filters, unscented Kalman filters, particle filt...
github.com
칼만필터란 무엇인가
공대 출신이라면 칼만필터를 한번쯤은 들어 보았을 것이다. 조금 더 관심을 가진 사람이라면 칼만필터가 다음과 같은 일을 한다고 들었을 것이다. 칼만필터로 신호에 섞인 노이즈를 제
pasus.tistory.com
'분석 Python > 구현 및 자료' 카테고리의 다른 글
| Python) featuretools를 사용한 자동 변수 생성 (0) | 2022.01.22 |
|---|---|
| Python) most frequent speed test (0) | 2021.12.24 |
| Python) 회귀 분석 기본 사용법 정리(scikit-learn, statsmodels) (2) | 2021.08.11 |
| notion-py를 사용하여 캘린더 만들기 (0) | 2021.08.08 |
| Python) Yield 에 대해서 알아보기 (0) | 2021.08.07 |