GAT는 Attention Aggregator를 사용하는 방식으로 위치는 다음과 같다.

GAT Layer 구현한 것을 따라 시행해봤다.

Equation (1) is a linear transformation of the lower layer embedding $h_i^{(l)}$ and $W^{(l)}$ is its learnable weight matrix. This transformation is useful to achieve a sufficient expressive power to transform input features (in our example one-hot vectors) into high-level and dense features.
Equation (2) computes a pair-wise unnormalized attention score between two neighbors. Here, it first concatenates the $z$ embeddings of the two nodes, where $||$ denotes concatenation, then takes a dot product of it and a learnable weight vector $\vec a^{(l)}$, and applies a LeakyReLU in the end. This form of attention is usually called additive attention, contrast with the dot-product attention in the Transformer model. The attention score indicates the importance of a neighbor node in the message passing framework.
Equation (3) applies a softmax to normalize the attention scores on each node’s incoming edges.
Equation (4) is similar to GCN. The embeddings from neighbors are aggregated together, scaled by the attention scores.
print('\n\n----- One-hot vector representation of nodes. Shape(n,n)\n')
X = np.eye(5, 5)
n = X.shape[0]
np.random.shuffle(X)
print(X)
print('\n\n----- Embedding dimension\n')
emb = 3
print(emb)
print('\n\n----- Weight Matrix. Shape(emb, n)\n')
W = np.random.uniform(-np.sqrt(1. / emb), np.sqrt(1. / emb), (emb, n))
print(W)
print('\n\n----- Adjacency Matrix (undirected graph). Shape(n,n)\n')
A = np.random.randint(2, size=(n, n))
np.fill_diagonal(A, 1)
A = (A + A.T)
A[A > 1] = 1
print(A)----- One-hot vector representation of nodes. Shape(n,n)
[[0 0 1 0 0] # node 1
[0 1 0 0 0] # node 2
[0 0 0 0 1]
[1 0 0 0 0]
[0 0 0 1 0]]
----- Embedding dimension
3
----- Weight Matrix. Shape(emb, n)
[[-0.4294049 0.57624235 -0.3047382 -0.11941829 -0.12942953]
[ 0.19600584 0.5029172 0.3998854 -0.21561317 0.02834577]
[-0.06529497 -0.31225734 0.03973776 0.47800217 -0.04941563]]
----- Adjacency Matrix (undirected graph). Shape(n,n)
[[1 1 1 0 1]
[1 1 1 1 1]
[1 1 1 1 0]
[0 1 1 1 1]
[1 1 0 1 1]]1. apply a parameterized linear transformation to every node
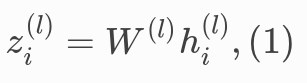
# equation (1)
print('\n\n----- Linear Transformation. Shape(n, emb)\n')
z1 = X.dot(W.T)
print(z1)
2. compute self attention coeff for each edge
The next operation is to introduce the self-attention coefficients for each edge.
# equation (2) - First part
print('\n\n----- Concat hidden features to represent edges. Shape(len(emb.concat(emb)), number of edges)\n')
edge_coords = np.where(A==1)
h_src_nodes = z1[edge_coords[0]]
h_dst_nodes = z1[edge_coords[1]]
z2 = np.concatenate((h_src_nodes, h_dst_nodes), axis=1)# equation (2) - Second part
print('\n\n----- Attention coefficients. Shape(1, len(emb.concat(emb)))\n')
att = np.random.rand(1, z2.shape[1])
print(att)
print('\n\n----- Edge representations combined with the attention coefficients. Shape(1, number of edges)\n')
z2_att = z2.dot(att.T)
print(z2_att)
print('\n\n----- Leaky Relu. Shape(1, number of edges)')
e = leaky_relu(z2_att)
print(e)## 또 다른 방법
z2를 다음과 같이 만들면, 모든 edge를 연결한 형태로 만들 수 있음.
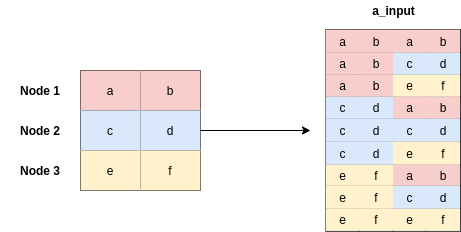
N = z1.shape[0]
z2 = np.concatenate((np.repeat(z1,N,axis=0).reshape(N*N,-1) , np.tile(z1, (N,1))),axis=1)
z2_att = z2.dot(att.T)
print(z2_att)
print('\n\n----- Leaky Relu. Shape(1, number of edges)')
e = leaky_relu(z2_att)
print(e)
3. Normalization (Softmax)
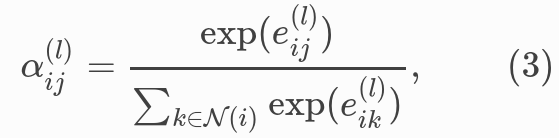
# equation (3)
print('\n\n----- Edge scores as matrix. Shape(n,n)\n')
e_matr = np.zeros(A.shape)
e_matr[edge_coords[0], edge_coords[1]] = e.reshape(-1,)
print(e_matr)
print('\n\n----- For each node, normalize the edge (or neighbor) contributions using softmax\n')
alpha0 = softmax(e_matr[:,0][e_matr[:,0] != 0])
alpha1 = softmax(e_matr[:,1][e_matr[:,1] != 0])
alpha2 = softmax(e_matr[:,2][e_matr[:,2] != 0])
alpha3 = softmax(e_matr[:,3][e_matr[:,3] != 0])
alpha4 = softmax(e_matr[:,4][e_matr[:,4] != 0])
alpha = np.concatenate((alpha0, alpha1, alpha2, alpha3, alpha4))
print(alpha)
print('\n\n----- Normalized edge score matrix. Shape(n,n)\n')
A_scaled = np.zeros(A.shape)
A_scaled[edge_coords[0], edge_coords[1]] = alpha.reshape(-1,)
print(A_scaled)
4. compute the neighborhood aggregation
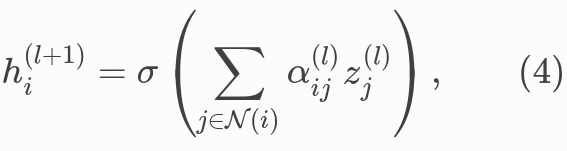
# equation (4)
print('\n\nNeighborhood aggregation (GCN) scaled with attention scores (GAT). Shape(n, emb)\n')
ND_GAT = A_scaled.dot(z1)
print(ND_GAT)
Pytorch Version
in_features = 5
out_features = 2
nb_nodes = 3
W = nn.Parameter(torch.zeros(size=(in_features, out_features))) #xavier paramiter inizializator
nn.init.xavier_uniform_(W.data, gain=1.414)
input = torch.rand(nb_nodes,in_features)
## 1 X 3 X 5
# linear transformation
h = torch.mm(input, W)
N = h.size()[0]
print(h.shape)
a = nn.Parameter(torch.zeros(size=(2*out_features, 1))) #xavier paramiter inizializator
nn.init.xavier_uniform_(a.data, gain=1.414)
print(a.shape)
leakyrelu = nn.LeakyReLU(0.2) # LeakyReLU
a_input = torch.cat([h.repeat(1, N).view(N * N, -1), h.repeat(N, 1)], dim=1).view(N, -1, 2 * out_features)
e = leakyrelu(torch.matmul(a_input, a).squeeze(2))
# Masked Attention
adj = torch.randint(2, (3, 3))
zero_vec = -9e15*torch.ones_like(e)
print(zero_vec.shape)
attention = torch.where(adj > 0, e, zero_vec)
print(adj,"\n",e,"\n",zero_vec)
attention = F.softmax(attention, dim=1)
h_prime = torch.matmul(attention, h)GAT LAYER IMPLEMENTATION
class GATLayer(nn.Module):
def __init__(self, in_features, out_features, dropout, alpha, concat=True):
super(GATLayer, self).__init__()
self.dropout = dropout # drop prob = 0.6
self.in_features = in_features #
self.out_features = out_features #
self.alpha = alpha # LeakyReLU with negative input slope, alpha = 0.2
self.concat = concat # conacat = True for all layers except the output layer.
# Xavier Initialization of Weights
# Alternatively use weights_init to apply weights of choice
self.W = nn.Parameter(torch.zeros(size=(in_features, out_features)))
nn.init.xavier_uniform_(self.W.data, gain=1.414)
self.a = nn.Parameter(torch.zeros(size=(2*out_features, 1)))
nn.init.xavier_uniform_(self.a.data, gain=1.414)
# LeakyReLU
self.leakyrelu = nn.LeakyReLU(self.alpha)
def forward(self, input, adj):
# Linear Transformation
h = torch.mm(input, self.W) # matrix multiplication
N = h.size()[0]
print(N)
# Attention Mechanism
a_input = torch.cat([h.repeat(1, N).view(N * N, -1), h.repeat(N, 1)], dim=1).view(N, -1, 2 * self.out_features)
e = self.leakyrelu(torch.matmul(a_input, self.a).squeeze(2))
# Masked Attention
zero_vec = -9e15*torch.ones_like(e)
attention = torch.where(adj > 0, e, zero_vec)
attention = F.softmax(attention, dim=1)
attention = F.dropout(attention, self.dropout, training=self.training)
h_prime = torch.matmul(attention, h)
if self.concat:
return F.elu(h_prime)
else:
return h_primePytorch-Geometric Version
from torch_geometric.data import Data
from torch_geometric.nn import GATConv
from torch_geometric.datasets import Planetoid
import torch_geometric.transforms as T
import matplotlib.pyplot as plt
name_data = 'Cora'
dataset = Planetoid(root= '/tmp/' + name_data, name = name_data)
dataset.transform = T.NormalizeFeatures()
print(f"Number of Classes in {name_data}:", dataset.num_classes)
print(f"Number of Node Features in {name_data}:", dataset.num_node_features)class GAT(torch.nn.Module):
def __init__(self):
super(GAT, self).__init__()
self.hid = 8
self.in_head = 8
self.out_head = 1
self.conv1 = GATConv(dataset.num_features, self.hid, heads=self.in_head, dropout=0.6)
self.conv2 = GATConv(self.hid*self.in_head, dataset.num_classes, concat=False,
heads=self.out_head, dropout=0.6)
def forward(self, data):
x, edge_index = data.x, data.edge_index
x = F.dropout(x, p=0.6, training=self.training)
x = self.conv1(x, edge_index)
x = F.elu(x)
x = F.dropout(x, p=0.6, training=self.training)
x = self.conv2(x, edge_index)
return F.log_softmax(x, dim=1)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
device = "cpu"
model = GAT().to(device)
data = dataset[0].to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.005, weight_decay=5e-4)
model.train()
for epoch in range(1000):
model.train()
optimizer.zero_grad()
out = model(data)
loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
if epoch%200 == 0:
print(loss)
loss.backward()
optimizer.step()
| content | url |
| gat 구현 | https://towardsdatascience.com/graph-attention-networks-under-the-hood-3bd70dc7a87 |
| pytorch-geometric tutorial3 (GAT) | https://github.com/AntonioLonga/PytorchGeometricTutorial |
'관심있는 주제 > GNN' 카테고리의 다른 글
| Python) Fraud detection with Graph Attention Networks (0) | 2022.01.28 |
|---|---|
| GNN) GCN Layer Implementation (0) | 2021.07.03 |
| GNN-자료 정리 (2) | 2021.07.03 |
| Paper) Learning to Simulate Complex Physics with Graph Networks (ICML 2020) (2) | 2021.06.22 |
| pytorch) Create Your Own GNN DataSets (1) | 2021.04.13 |