파이썬에서 genetic algorithm을 사용하는 패키지들을 다 사용해보진 않았지만, 확장성이 있어 보이고, 시도할 일이 있어서 살펴봤다.
이 패키지에서 가장 인상 깊었던 것은 neural network에서 hyper parameter 탐색을 gradient descent 방식이 아닌 GA로도 할 수 있다는 것이다.
개인적으로 이 부분이 어느정도 초기치를 잘 잡아줄 수 있는 역할로도 쓸 수 있고, Loss가 gradient descent 하기 어려운 구조에서 대안으로 쓸 수 있을 것으로도 생각된다.
일단 큰 흐름은 다음과 같이 된다.
사실 완전히 흐름이나 각 parameter에 대한 이해는 부족한 상황

import pygad
import numpy
function_inputs = [4,-2,3.5,5,-11,-4.7]
desired_output = 44
def fitness_func(solution, solution_idx):
output = numpy.sum(solution*function_inputs)
fitness = 1.0 / (numpy.abs(output - desired_output) + 0.000001)
return fitness
fitness_function = fitness_func
def on_start(ga_instance):
print("on_start()")
def on_fitness(ga_instance, population_fitness):
print("on_fitness()")
def on_parents(ga_instance, selected_parents):
print("on_parents()")
def on_crossover(ga_instance, offspring_crossover):
print("on_crossover()")
def on_mutation(ga_instance, offspring_mutation):
print("on_mutation()")
def on_generation(ga_instance):
print("on_generation()")
def on_stop(ga_instance, last_population_fitness):
print("on_stop()")
ga_instance = pygad.GA(num_generations=3,
num_parents_mating=5,
fitness_func=fitness_function,
sol_per_pop=10,
num_genes=len(function_inputs),
on_start=on_start,
on_fitness=on_fitness,
on_parents=on_parents,
on_crossover=on_crossover,
on_mutation=on_mutation,
on_generation=on_generation,
on_stop=on_stop)
ga_instance.run()## 결과
num_generatrion3을 3을 하니 각 함수의 반복이 3번이 나오는 것을 알 수 있다.
on_start()
on_fitness()
on_parents()
on_crossover()
on_mutation()
on_generation()
on_fitness()
on_parents()
on_crossover()
on_mutation()
on_generation()
on_fitness()
on_parents()
on_crossover()
on_mutation()
on_generation()
on_stop()Fitting a Linear Model

import pygad
import numpy
"""
Given the following function:
y = f(w1:w6) = w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + 6wx6
where (x1,x2,x3,x4,x5,x6)=(4,-2,3.5,5,-11,-4.7) and y=44
What are the best values for the 6 weights (w1 to w6)? We are going to use the genetic algorithm to optimize this function.
"""function_inputs = [4,-2,3.5,5,-11,-4.7] # Function inputs.
desired_output = 44 # Function output.fitness_func
fitness_func은 maximize를 기준으로 하는 함수를 설계하면 된다.
해당 함수를 구성할 때는 gradient를 고려하지 않고 단순히 결괏값만 사용하여 파라미터를 탐색할 수 있게 된다.
def fitness_func(solution, solution_idx):
# Calculating the fitness value of each solution in the current population.
# The fitness function calulates the sum of products between each input and its corresponding weight.
output = numpy.sum(solution*function_inputs)
fitness = 1.0 / numpy.abs(output - desired_output)
return fitness- num_generations: Number of generations.
- num_parents_mating: Number of solutions to be selected as parents.
- fitness_func: Accepts a function that must accept 2 parameters (a single solution and its index in the population) and return the fitness value of the solution. Available starting from PyGAD 1.0.17 until 1.0.20 with a single parameter representing the solution. Changed in PyGAD 2.0.0 and higher to include a second parameter representing the solution index. Check the Preparing the ``fitness_func`` Parameter section for information about creating such a function.
fitness_function = fitness_func
num_generations = 100 # Number of generations.
num_parents_mating = 7 # Number of solutions to be selected as parents in the mating pool.- initial_population : # To prepare the initial population, there are 2 ways:
# 1) Prepare it yourself and pass it to the initial_population parameter. This way is useful when the user wants to start the genetic algorithm with a custom initial population.
# 2) Assign valid integer values to the sol_per_pop and num_genes parameters. If the initial_population parameter exists, then the sol_per_pop and num_genes parameters are useless.
초기 모집단을 설정해 놓으면 sel_per_pop 과 num_gens은 무시
- sol_per_pop: Number of solutions (i.e. chromosomes) within the population. This parameter has no action if initial_population parameter exists. (모집단으로써 제안된 설루션)
- num_genes: Number of genes in the solution/chromosome. This parameter is not needed if the user feeds the initial population to the initial_population parameter.

sol_per_pop = 50 # Number of solutions in the population.
num_genes = len(function_inputs)
- init_range_low=-4: The lower value of the random range from which the gene values in the initial population are selected. init_range_low defaults to -4. Available in PyGAD 1.0.20 and higher. This parameter has no action if the initial_population parameter exists. (탐색 공간 의미)
- init_range_high=4: The upper value of the random range from which the gene values in the initial population are selected. init_range_high defaults to +4. Available in PyGAD 1.0.20 and higher. This parameter has no action if the initial_population parameter exists. (탐색 공간 의미)
- gene_type=float: Controls the gene type. It has an effect only when the parameter gene_space is None (which is its default value). Starting from PyGAD 2.9.0, the gene_type parameter can be assigned to a numeric value of any of these types: int, float, and numpy.int/uint/float(8-64).
- 탐색 공간을 연속형, interger 다 가능함!
init_range_low = -2
init_range_high = 5- parent_selection_type="sss": The parent selection type. Supported types are sss (for steady-state selection), rws (for roulette wheel selection), sus (for stochastic universal selection), rank (for rank selection), random (for random selection), and tournament (for tournament selection).
- keep_parents=-1: Number of parents to keep in the current population. -1 (default) means to keep all parents in the next population. 0 means keep no parents in the next population. A value greater than 0 means keeps the specified number of parents in the next population. Note that the value assigned to keep_parents cannot be < - 1 or greater than the number of solutions within the population sol_per_pop.
- K_tournament=3: In case that the parent selection type is tournament, the K_tournament specifies the number of parents participating in the tournament selection. It defaults to 3.
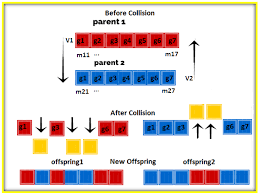
- crossover_type="single_point": Type of the crossover operation. Supported types are single_point (for single-point crossover), two_points (for two points crossover), uniform (for uniform crossover), and scattered (for scattered crossover). Scattered crossover is supported from PyGAD 2.9.0 and higher. It defaults to single_point. Starting from PyGAD 2.2.2 and higher, if crossover_type=None, then the crossover step is bypassed which means no crossover is applied and thus no offspring will be created in the next generations. The next generation will use the solutions in the current population.
parent_selection_type = "sss" # Type of parent selection.
keep_parents = 7 # Number of parents to keep in the next population. -1 means keep all parents and 0 means keep nothing.
crossover_type = "single_point" # Type of the crossover operator.
# Parameters of the mutation operation.
mutation_type = "random" # Type of the mutation operator.
mutation_percent_genes = 10 # Percentage of genes to mutate. This parameter has no action if the parameter mutation_num_genes exists or when mutation_type is None.
last_fitness = 0
def callback_generation(ga_instance):
global last_fitness
print("Generation = {generation}".format(generation=ga_instance.generations_completed))
print("Fitness = {fitness}".format(fitness=ga_instance.best_solution()[1]))
print("Change = {change}".format(change=ga_instance.best_solution()[1] - last_fitness))
last_fitness = ga_instance.best_solution()[1]- random_mutation_min_val=-1.0: For random mutation, the random_mutation_min_val parameter specifies the start value of the range from which a random value is selected to be added to the gene. It defaults to -1. Starting from PyGAD 2.2.2 and higher, this parameter has no action if mutation_type is None.
- random_mutation_max_val=1.0: For random mutation, the random_mutation_max_val parameter specifies the end value of the range from which a random value is selected to be added to the gene. It defaults to +1. Starting from PyGAD 2.2.2 and higher, this parameter has no action if mutation_type is None.
- gene_space=None: It is used to specify the possible values for each gene in case the user wants to restrict the gene values. It is useful if the gene space is restricted to a certain range or to discrete values. It accepts a list, tuple, range, or numpy.ndarray. When all genes have the same global space, specify their values as a list/tuple/range/numpy.ndarray. For example, gene_space = [0.3, 5.2, -4, 8] restricts the gene values to the 4 specified values. If each gene has its own space, then the gene_space parameter can be nested like [[0.4, -5], [0.5, -3.2, 8.2, -9],...] where the first sublist determines the values for the first gene, the second sublist for the second gene, and so on. If the nested list/tuple has a None value, then the gene’s initial value is selected randomly from the range specified by the 2 parameters init_range_low and init_range_high and its mutation value is selected randomly from the range specified by the 2 parameters random_mutation_min_val and random_mutation_max_val. gene_space is added in PyGAD 2.5.0. Check the Release History section of the documentation for more details. In PyGAD 2.9.0, NumPy arrays can be assigned to the gene_space parameter.
- 각 gene 별로 범위를 제약할 수 있어서 integer나 특정 constraint이 있는 경우 유용해 보임
아직 GA에 대한 완전한 이해가 부족하다 보니 파라미터 각각의 의미를 느낌적으로만 알고 있다. 실제로 적용한다고 했을 때 본격적으로 파봐야 할 것 같다.
GA INSTANCE 생성
last_fitness = 0
def callback_generation(ga_instance):
global last_fitness
print("Generation = {generation}".format(generation=ga_instance.generations_completed))
print("Fitness = {fitness}".format(fitness=ga_instance.best_solution()[1]))
print("Change = {change}".format(change=ga_instance.best_solution()[1] - last_fitness))
last_fitness = ga_instance.best_solution()[1]
# Creating an instance of the GA class inside the ga module. Some parameters are initialized within the constructor.
ga_instance = pygad.GA(num_generations=num_generations,
num_parents_mating=num_parents_mating,
fitness_func=fitness_function,
sol_per_pop=sol_per_pop,
num_genes=num_genes,
init_range_low=init_range_low,
init_range_high=init_range_high,
parent_selection_type=parent_selection_type,
keep_parents=keep_parents,
crossover_type=crossover_type,
mutation_type=mutation_type,
mutation_percent_genes=mutation_percent_genes,
on_generation=callback_generation)
RUN
# Running the GA to optimize the parameters of the function.
ga_instance.run()
# After the generations complete, some plots are showed that summarize the how the outputs/fitenss values evolve over generations.
ga_instance.plot_result()
# Returning the details of the best solution.
solution, solution_fitness, solution_idx = ga_instance.best_solution()
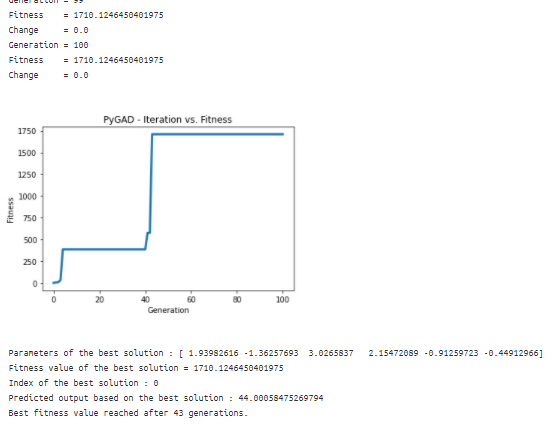
print("Parameters of the best solution : {solution}".format(solution=solution))
print("Fitness value of the best solution = {solution_fitness}".format(solution_fitness=solution_fitness))
print("Index of the best solution : {solution_idx}".format(solution_idx=solution_idx))
prediction = numpy.sum(numpy.array(function_inputs)*solution)
print("Predicted output based on the best solution : {prediction}".format(prediction=prediction))
if ga_instance.best_solution_generation != -1:
print("Best fitness value reached after {best_solution_generation} generations.".format(best_solution_generation=ga_instance.best_solution_generation))
저장
해당 instance를 저장하여 재사용할 수 있다는 게 제공한다.
# Saving the GA instance.
filename = 'genetic' # The filename to which the instance is saved. The name is without extension.
ga_instance.save(filename=filename)
재사용
# Loading the saved GA instance.
loaded_ga_instance = pygad.load(filename=filename)
loaded_ga_instance.run()
loaded_ga_instance.plot_result()
solution, solution_fitness, solution_idx = loaded_ga_instance.best_solution()
다음 시간에는 pytorch를 이용해서 재사용 후에 해당 초기치를 저장 후 skorch로 재사용하는 것을 해보려고 한다.
Full Code
import pygad
import numpy
function_inputs = [4,-2,3.5,5,-11,-4.7] # Function inputs.
desired_output = 44 # Function output.
def fitness_func(solution, solution_idx):
# Calculating the fitness value of each solution in the current population.
# The fitness function calulates the sum of products between each input and its corresponding weight.
output = numpy.sum(solution*function_inputs)
fitness = 1.0 / numpy.abs(output - desired_output)
return fitness
fitness_function = fitness_func
num_generations = 100 # Number of generations.
num_parents_mating = 7 # Number of solutions to be selected as parents in the mating pool.
# To prepare the initial population, there are 2 ways:
# 1) Prepare it yourself and pass it to the initial_population parameter. This way is useful when the user wants to start the genetic algorithm with a custom initial population.
# 2) Assign valid integer values to the sol_per_pop and num_genes parameters. If the initial_population parameter exists, then the sol_per_pop and num_genes parameters are useless.
sol_per_pop = 50 # Number of solutions in the population.
num_genes = len(function_inputs)
init_range_low = -2
init_range_high = 5
parent_selection_type = "sss" # Type of parent selection.
keep_parents = 7 # Number of parents to keep in the next population. -1 means keep all parents and 0 means keep nothing.
crossover_type = "single_point" # Type of the crossover operator.
# Parameters of the mutation operation.
mutation_type = "random" # Type of the mutation operator.
mutation_percent_genes = 10 # Percentage of genes to mutate. This parameter has no action if the parameter mutation_num_genes exists or when mutation_type is None.
last_fitness = 0
def callback_generation(ga_instance):
global last_fitness
print("Generation = {generation}".format(generation=ga_instance.generations_completed))
print("Fitness = {fitness}".format(fitness=ga_instance.best_solution()[1]))
print("Change = {change}".format(change=ga_instance.best_solution()[1] - last_fitness))
last_fitness = ga_instance.best_solution()[1]
# Creating an instance of the GA class inside the ga module. Some parameters are initialized within the constructor.
ga_instance = pygad.GA(num_generations=num_generations,
num_parents_mating=num_parents_mating,
fitness_func=fitness_function,
sol_per_pop=sol_per_pop,
num_genes=num_genes,
init_range_low=init_range_low,
init_range_high=init_range_high,
parent_selection_type=parent_selection_type,
keep_parents=keep_parents,
crossover_type=crossover_type,
mutation_type=mutation_type,
mutation_percent_genes=mutation_percent_genes,
on_generation=callback_generation)
# Running the GA to optimize the parameters of the function.
ga_instance.run()
# After the generations complete, some plots are showed that summarize the how the outputs/fitenss values evolve over generations.
ga_instance.plot_result()
# Returning the details of the best solution.
solution, solution_fitness, solution_idx = ga_instance.best_solution()
print("Parameters of the best solution : {solution}".format(solution=solution))
print("Fitness value of the best solution = {solution_fitness}".format(solution_fitness=solution_fitness))
print("Index of the best solution : {solution_idx}".format(solution_idx=solution_idx))
prediction = numpy.sum(numpy.array(function_inputs)*solution)
print("Predicted output based on the best solution : {prediction}".format(prediction=prediction))
if ga_instance.best_solution_generation != -1:
print("Best fitness value reached after {best_solution_generation} generations.".format(best_solution_generation=ga_instance.best_solution_generation))
# Saving the GA instance.
filename = 'genetic' # The filename to which the instance is saved. The name is without extension.
ga_instance.save(filename=filename)
# Loading the saved GA instance.
loaded_ga_instance = pygad.load(filename=filename)
loaded_ga_instance.run()
loaded_ga_instance.plot_result()
solution, solution_fitness, solution_idx = loaded_ga_instance.best_solution()
solution
pygad.readthedocs.io/en/latest/README_pygad_ReadTheDocs.html#init
pygad Module — PyGAD 2.10.2 documentation
pygad Module This section of the PyGAD’s library documentation discusses the pygad module. Using the pygad module, instances of the genetic algorithm can be created, run, saved, and loaded. pygad.GA Class The first module available in PyGAD is named pyga
pygad.readthedocs.io
github.com/ahmedfgad/GeneticAlgorithmPython
ahmedfgad/GeneticAlgorithmPython
Build the Genetic Algorithm in Python 3 using NumPy - ahmedfgad/GeneticAlgorithmPython
github.com
blog.paperspace.com/genetic-algorithm-applications-using-pygad/
5 Genetic Algorithm Applications Using PyGAD | Paperspace Blog
PyGAD is an open-source Python library for implementing the genetic algorithm. In this tutorial we'll cover 5 simple machine learning projects with PyGAD.
blog.paperspace.com
towardsdatascience.com/feature-reduction-using-genetic-algorithm-with-python-403a5f4ef 0c1
Feature Reduction using Genetic Algorithm with Python
Using Python to use genetic algorithm for reducing the feature vector length and training random forest by the reduced vector.
towardsdatascience.com
towardsdatascience.com/introduction-to-genetic-algorithms-including-example-code-e396e98d8bf3
Introduction to Genetic Algorithms — Including Example Code
A genetic algorithm is a search heuristic that is inspired by Charles Darwin’s theory of natural evolution. This algorithm reflects the…
towardsdatascience.com
towardsdatascience.com/gas-and-nns-6a41f1e8146d
Genetic Algorithms + Neural Networks = Best of Both Worlds
Learn how Neural Network training can be accelerated using Genetic Algorithms!
towardsdatascience.com
'분석 Python > Packages' 카테고리의 다른 글
| Python Pkg) array를 gif로 바꿔주는 패키지 (0) | 2021.05.13 |
|---|---|
| google에서 만든 NAS 패키지 Model Search (0) | 2021.02.24 |
| OR-Tools (Google Optimization Tools) (0) | 2020.10.24 |
| [Python] package 설치 및 인터넷 없이 설치하는 방법 (0) | 2020.09.16 |
| [Python] XAI 패키지 조사 해보기 (eXplainable AI) (0) | 2020.09.14 |