아시다시피 실제 데이터에는 잡음이 있다.
상당히 짜증스럽기는 하지만, 그러한 잡음은 데이터의 기원에 대한 더 넓은 시야를 제공하기 때문에 의미가 있다.
타겟 값은 인풋에 따라서 잡음의 정도가 다를 수 있기 때문이다. 그리고 그것은 데이터를 이해하는 데 있어서 주요한 영향을 끼친다.
$$f(x)= x^2 -6x+9$$
위와 같은 함수가 잇다고 하자. 위의 함수는 determinsitc output $f(x)$를 가진다.
그러나 실제 데이터에서는 잡음이 생길 수 있는데, 여기서는 x 가 커질수록 잡음이 더 증가한다고 하자
그러면 아래와 같은 그림을 가질 것이다
$$g(x) = f(x) + \epsilon(x)$$
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
import matplotlib.pyplot as plt
from sklearn.utils import shuffle
def f(x):
return x**2-6*x+9
def data_generator(x,sigma_0,samples):
return np.random.normal(f(x),sigma_0*x,samples)
sigma_0 = 0.1
x_vals = np.arange(1,5.2,0.2)
x_arr = np.array([])
y_arr = np.array([])
samples = 50
for x in x_vals:
x_arr = np.append(x_arr, np.full(samples,x))
y_arr = np.append(y_arr, data_generator(x,sigma_0,samples))
x_arr, y_arr = shuffle(x_arr, y_arr)
x_test = np.arange(1.1,5.1,0.2)
fig, ax = plt.subplots(figsize=(10,10))
plt.grid(True)
plt.xlabel('x')
plt.ylabel('g(x)')
ax.scatter(x_arr,y_arr,label='sampled data')
ax.plot(x_vals,f(x_vals),c='m',label='f(x)')
ax.legend(loc='upper center',fontsize='large',shadow=True)
plt.show()
보라색 선은 잡음이 없을 때의 $f(x)$를 의미한다.
만약 여기서 우리가 f(x)를 추정하고 싶다 하면 아래와 같은 네트워크를 구성할 것이다.
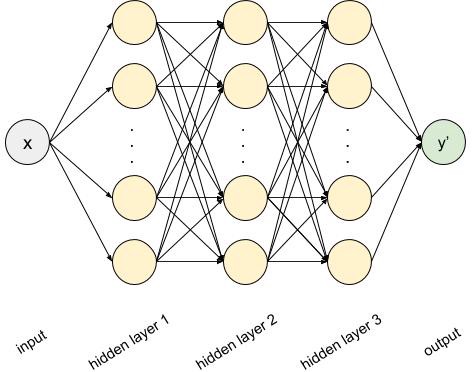
epochs = 500
batch_size = 50
learning_rate = 0.0003
display_step = 50
batch_num = int(len(x_arr) / batch_size)
tf.reset_default_graph()
x = tf.placeholder(name='x',shape=(None,1),dtype=tf.float32)
y = tf.placeholder(name='y',shape=(None,1),dtype=tf.float32)
layer = x
for _ in range(3):
layer = tf.layers.dense(inputs=layer, units=12, activation=tf.nn.tanh)
output = tf.layers.dense(inputs=layer, units=1)cost = tf.reduce_mean(tf.losses.mean_squared_error(labels=y,predictions=output))
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)
x_batches = np.array_split(x_arr, batch_num)
y_batches = np.array_split(y_arr, batch_num)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for epoch in range(epochs):
avg_cost = 0.0
x_batches, y_batches = shuffle(x_batches, y_batches)
for i in range(batch_num):
x_batch = np.expand_dims(x_batches[i],axis=1)
y_batch = np.expand_dims(y_batches[i],axis=1)
_, c = sess.run([optimizer,cost], feed_dict={x:x_batch, y:y_batch})
avg_cost += c/batch_num
if epoch % display_step == 0:
print('Epoch {0:4d} | cost = {1:.4f}'.format(epoch,avg_cost))
y_pred = sess.run(output,feed_dict={x:np.expand_dims(x_test,axis=1)})
print('Final cost: {0:.4f}'.format(avg_cost))
fig, ax = plt.subplots(figsize=(10,10))
plt.grid(True)
plt.xlabel('x')
plt.ylabel('y')
ax.scatter(x_arr,y_arr,c='b',label='sampled data')
ax.scatter(x_test,y_pred,c='r',label='predicted values')
ax.plot(x_vals,f(x_vals),c='m',label='f(x)')
ax.legend(loc='upper center',fontsize='large',shadow=True)
plt.show()
일반적으로 적용하면 $f(X)$를 잘 배운것을 알 수 있다!
하지만 각 점에 대한 잡음에 대해서는 추정하지 못했다.
이럴 때 MDN을 사용해서 잡음까지도 고려한 모델링을 할 수 있게 된다.
여기서는 잡음을 가우시안으로 가정하기 때문에 각 점에 대한 평균과 표준편차를 추정하는 모델링은 다음과 같다.
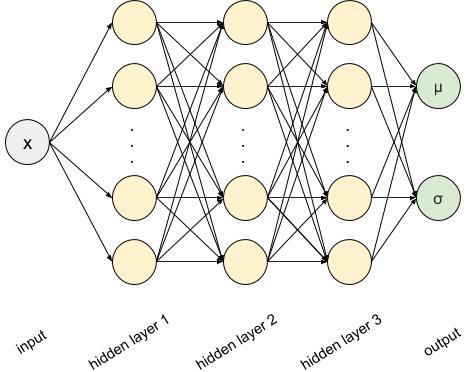
x = tf.placeholder(name='x',shape=(None,1),dtype=tf.float32)
layer = x
for _ in range(3):
layer = tf.layers.dense(inputs=layer, units=12, activation=tf.nn.tanh)
mu = tf.layers.dense(inputs=layer, units=1)
sigma = tf.layers.dense(inputs=layer, units=1,activation=lambda x: tf.nn.elu(x) + 1)이제 그러면 손실 함수를 정의할 필요가 잇을 것이다.
지금 아웃풋은 결국 평균과 표준편차를 추정했다. 이것들은 아시다시피 가우시안의 파라미터들이다.
이제 이렇게 추정된 파라미터들로 가우시안을 샘플링할 수 있고 이것을 타겟값과의 확률을 최대화하는 방향으로 학습을 시킨다. 결국 그렇게 함으로써, 타겟값과 가까워지게 평균과 표준편차를 학습할 것이다.

def mdn_cost(mu, sigma, y):
dist = tf.distributions.Normal(loc=mu, scale=sigma)
return tf.reduce_mean(-dist.log_prob(y))epochs = 2000
batch_size = 50
learning_rate = 0.0003
display_step = 50
batch_num = int(len(x_arr) / batch_size)
tf.reset_default_graph()
x = tf.placeholder(name='x',shape=(None,1),dtype=tf.float32)
y = tf.placeholder(name='y',shape=(None,1),dtype=tf.float32)
layer = x
for _ in range(3):
layer = tf.layers.dense(inputs=layer, units=12, activation=tf.nn.tanh)
mu = tf.layers.dense(inputs=layer, units=1)
sigma = tf.layers.dense(inputs=layer, units=1, activation=lambda x: tf.nn.elu(x) + 1)
cost = mdn_cost(mu, sigma, y)
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)
x_batches = np.array_split(x_arr, batch_num)
y_batches = np.array_split(y_arr, batch_num)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for epoch in range(epochs):
avg_cost = 0.0
x_batches, y_batches = shuffle(x_batches, y_batches)
for i in range(batch_num):
x_batch = np.expand_dims(x_batches[i],axis=1)
y_batch = np.expand_dims(y_batches[i],axis=1)
_, c = sess.run([optimizer,cost], feed_dict={x:x_batch, y:y_batch})
avg_cost += c/batch_num
if epoch % display_step == 0:
print('Epoch {0:04d} | cost = {1:.4f}'.format(epoch,avg_cost))
mu_pred, sigma_pred = sess.run([mu,sigma],feed_dict={x:np.expand_dims(x_test,axis=1)})
print('Final cost: {0:.4f}'.format(avg_cost))그래서 아래 그림을 보면 x가 작을 때는 표준편차가 작게 학습이 되고 x가 클수록 편차가 커지는 것을 그대로 반영해서 학습한다는 것을 알 수 있다!
fig, ax = plt.subplots(figsize=(10,10))
plt.grid(True)
plt.xlabel('x')
plt.ylabel('y')
ax.errorbar(x_test,mu_pred,yerr=np.absolute(sigma_pred),c='r',ls='None',marker='.',ms=10,label='predicted distributions')
ax.scatter(x_arr,y_arr,c='b',alpha=0.05,label='sampled data')
ax.errorbar(x_vals,f(x_vals),yerr=x_vals * sigma_0,
c='b',lw=2,ls='None',marker='.',ms=10,label='true distributions')
ax.plot(x_vals,f(x_vals),c='m',label='f(x)')
ax.legend(loc='upper center',fontsize='large',shadow=True)
plt.show()
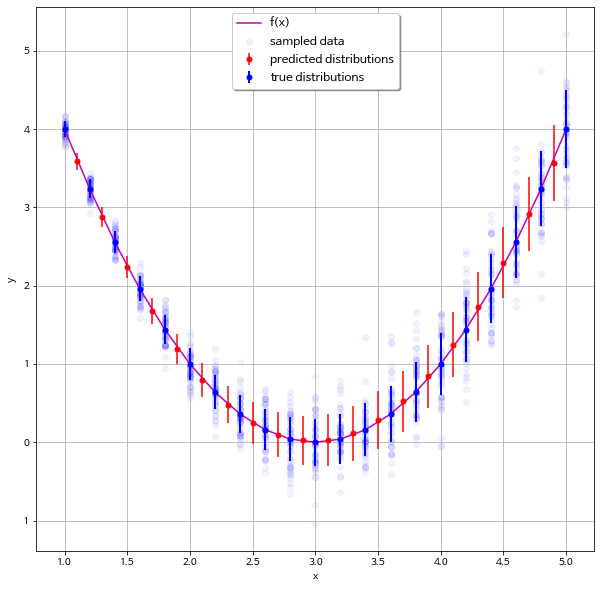
이런식으로 단일 값 추정이 아닌 분포 추정을 할 수 있다는 게 MDN의 큰 장점이고, 활용가치가 많아 보인다.
https://github.com/taboola/mdn-tensorflow-notebook-example
taboola/mdn-tensorflow-notebook-example
Contribute to taboola/mdn-tensorflow-notebook-example development by creating an account on GitHub.
github.com
'분석 Python > Tensorflow' 카테고리의 다른 글
| [Keras] EarlyStopping 및 Model 저장하기 (0) | 2020.11.21 |
|---|---|
| [Keras] Weighted Cross Entropy 적용하는 방법 (0) | 2020.11.21 |
| tf.layers.dense 알아보기 (tf.tensordot ,tf.matmul) (0) | 2020.04.24 |
| Learning from Multimodal Target 리뷰 (MDN)(Tensorflow) (0) | 2020.04.19 |
| tf.py_func 사용해보기 (0) | 2020.04.17 |