광고 한 번씩 눌러주세요! 블로그 운영에 큰 힘이 됩니다 :)

드디어 Mixture Density Neural Network 관련 코드를 찾았다.
필자는 혼합 분포 뉴럴 네트워크에 대한 것을 알고 싶었는데, 찾고 싶을 때는 죽어도 안 나오더니, 우연찮게 글을 찾게 되어 읽어보고 실습을 해보고 나중에 어떻게 써먹을지 생각을 해봐야겠다.
필자는 개인적으로 기대하는 방향은 VAE 같은 곳에 단순 가우시안으로 계산하는 방법이 아닌 Mixture density를 latent space에서 배우게 하고 싶다. 물론 실제로 그런 loss 함수 부분을 정의하는 방법도 또 찾아봐야겠지만, 이미 누군가는 다 해놨을 거라고 생각하고 열심히 찾아볼 계획이다. :)
Introduction
모델 평가를 위해 예측하고 불확실성을 측정하는 것은 사업상 이유 뿐만 아니라 통계적인 이유에서도 굉장히 중요하다.
기본적으로 지도 학습 모델에서는 예측하는 모형 $f(x)$와 정답 $y$가 있으며, 모형 $f(x)$를 사용하여 정답을 맞히기 위해 노력하고 얼마나 잘 예측했는지 수량화하려고 한다.
이는 일반적으로 범주 형 변수에 대한 연속 예측 변수 또는 사후 확률의 경우 모든 예측 변수에 대해 대략 평균을 출력하는 제곱합 또는 교차 엔트로피 오류 함수를 최소화하여 수행한다.
Business Case example
손 시계를 판매하고 판매자가 판매 할 제품을 나열하고 구매자가 해당 제품을 쇼핑하기 위해 방문하는 전형적인 아마존 유형 비즈니스 모델을 보유한 전자 상거래 회사 (ABC)를 생각해보자. ABC는 다른 판매자가 유사한 제품을 나열하려고 할 때 권장 가격을 만들기 위해 제품 목록 가격을 모델링하려고 한다.
아래 그림이 디지털 시계의 목록 가격의 분포라고 하자.

분포를 봤을 때, 디지털 시계는 20~2500 달러에서 팔린다. 시계를 판매하는 판매자는 3 가지 가격대이다. 20-500 / 700-1500 / 1600-2500 데이터의 타입은 선형 회귀의 단봉형 정규성 가정을 위반하고 있다.
그러나 실제 시나리오에서는 경험적 분포가 여전히 정규 분포이므로 기본 분포를 모른다.
Fitting a model and violation of assumptions
시계 유형을 예측 변수로만 사용하여 선형 회귀 모델을 적합하게 하면 1 번째 유형의 시계를 과대 예측하고 3 번째 유형의 시계를 과소 예측하여 디지털 유형 시계의 경우 1133 $을 예측한다.
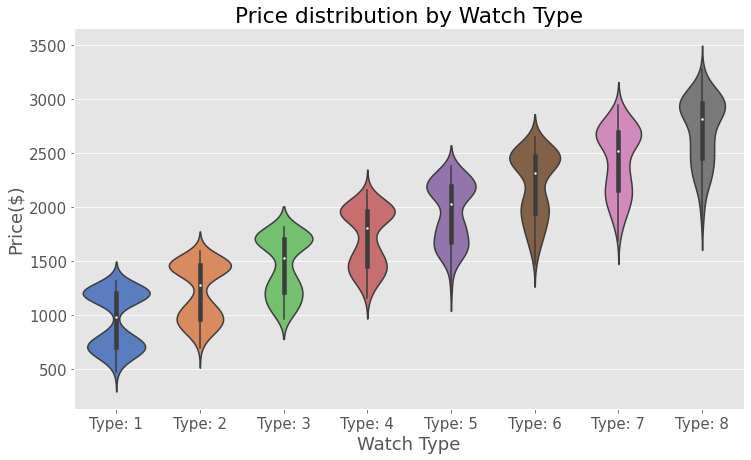
모든 시계 타입은 다른 수준과 다른 분산을 가지는 모드를 2개 가진 분포를 띄고 있다. 카테고리에 따라 시계 유형에 따라 분산의 차이가 있게 된다.
신경망 네트워크 또는 선형 회귀 분석을 시계 유형 만 예측 변수로 사용하여 이 데이터에 적합하면 예측 및 표준 오차 편차는 어떻게 될까?
데이터는 회귀 분석의 모든 가정을 따르지 않겠는가?

기본적으로, 선형 함수나 Ssum of squares를 최소화할 때, squared error term $^\mu(x,\theta) - y)^2$를 줄일 것이다. $x$에 의존하고 Homoscedasticity라고 도하는 나머지 매개 변수 (표준 편차)를 버리는 유일한 $\mu$를 얻게 될 것이다.
시계 타입에 따른 다중 모드 분포 파라미터를 학습할 수 있을까?
> 해결 방법은 MDN을 사용하는 것이라고 한다.
Gaussian Mixture Model and Mixture Density Network(MDN)
많은 사람들이 GMM은 알고 있을 것이다. GMM은 MDN과 매우 유사하기 때문에 MDN과 대조하기 위해 설명한다.
GMM은 expectaion-maximization을 사용하는 unsupervised learning algorithm 이고 이런 것 중에서는 K-means가 있다. K-means는 중복되는 군집이 있을 경우 작동하지 않지만, 반면에 GMM은 중복되는 군집에서도 기반한 분포의 파라미터를 학습함으로써, 학습할 수 있다.
위의 예제에 있는 그림에서 GMM을 적용함으로써 모드를 3개 가지는 파라미터를 이끌어낼 수 있다.
이론적으로 GMM은 n 개의 군집에 대한 구성요소를 계산한다($\mu, \sigma$) 주어진 확률분포에 대해서 최적화함으로써, 군집의 구성 요소를 할당한다.
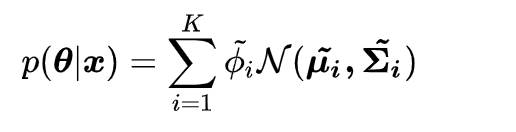
위에 식에서 $K$는 군집의 개수이다 $\phi$는 군집의 잠재된 확률을 의미한다. EM을 사용하여, GMM은 $\phi, \mu, \sigma$를 학습할 수 있다.
ABC예제에서, 1500*3[#N * 군집의 개수] $\phi$와 함께 3개의 $\mu$ 와 $\sigma$를 계산한다.
이해를 돕기 위해 위의 데이터 세트에 대해 GMM을 교육하고 군집 및 시그마가 실제 mu 및 신호에 가까운 지 확인했다고 한다.

MDN (Mixture Density Network)의 기반을 구축합니다. 예측 변수에 따라 모델 커널 매개 변수를 학습할 수 있다. 이를 위해 커널을 가우스 커널로 제한한다.
MDN은 GMM과 동일한 우도 함수를 최적화하고 데이터 세트의 각 샘플에 대해 mu, sigma 및 phi를 출력한다.

수하적인 디테일 없이, 바로 훈련!
Building and training MDN
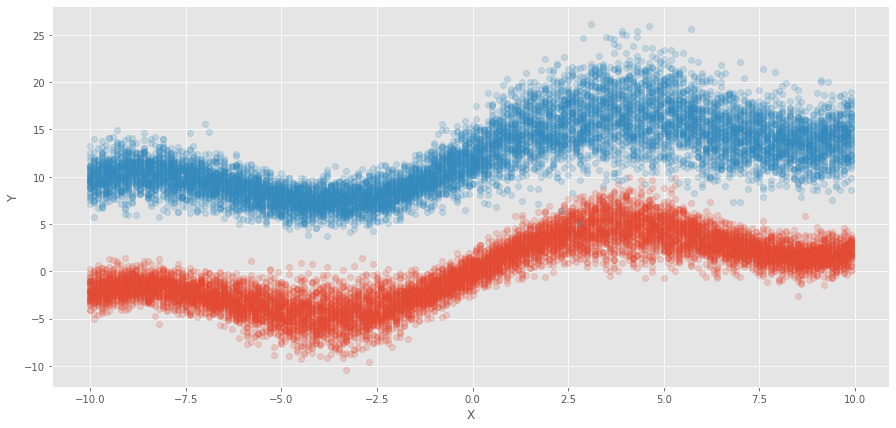
이런 식으로 데이터를 만들었다고 하자.
x_ = sin(0.5 * x) * 3.0+ x * 0.5)
f1(x) = N(x_, square(x_)/15) + N(0,1) # Cluster 1 y
f2(x) = N(f1(x) + 12, square(x)/100) + N(0,1) # Cluster 2 y
This equation generates data with 2 distinct cluster and x dependent variance.
실제로 만약 저러한 상황을 모른다고 하면 다음과 같이 그려질 것이다.
만약 실제 응용시, 아래와 같은 그림이 나올 경우 단순 회귀보다는 아무래도 MDN이 적합할 것이다.
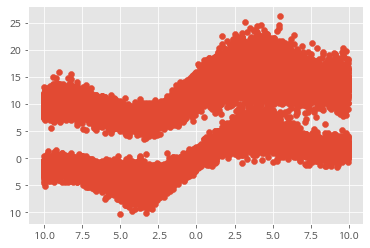
일단 MLP로 적합하면 다음과 같다.

그러면 딱 2개의 큰 라인에서 중간을 적합하고 있다.
그러므로 단순 MLP로 하게 되면, 뭘 해도 안된다라는 의미이다.
이제 MDN을 하는 것을 구경해보자.
import tensorflow as tf
import tensorflow_probability as tfp
## tensorflow 1.5를 사용하면 tensorflow_probability==0.7 설치해야 함.
class Network:
def __init__(self, x, y, K=50):
self.x = x
self.layer_1 = tf.layers.dense(x, units=50, activation=tf.nn.tanh)
self.layer_2 = tf.layers.dense(self.layer_1, units=20, activation=tf.nn.tanh)
self.layer_3 = tf.layers.dense(self.layer_2, units=20, activation=tf.nn.tanh)
self.layer_4 = tf.layers.dense(self.layer_3, units=20, activation=tf.nn.tanh)이 첫번째 부분에서는 기존에 mlp 코드 만든 것처럼 열심히 만들면 된다. 여기서는 (50,20,20,20)으로 나타냈다.
self.mu = tf.layers.dense(self.layer_4, units=K, activation=None, name="mu")
self.var = tf.exp(tf.layers.dense(self.layer_4, units=K, activation=tf.nn.softplus, name="sigma"))
self.pi = tf.layers.dense(self.layer_4, units=K, activation=tf.nn.softmax, name="pi")이제 이 두 번째 부분에서 $K$ 사이즈의 벡터 $\mu, \sigma, \phi$를 만들었다.
여기 예제에서는 큰 줄기가 2개이니 $K=2$일 것이다.
- $\mu$를 만들 때는 특별한 activation을 사용하지 않고 logit 값을 사용한다.
- $\sigma$를 만들 때는 음수가 나오면 안 되니 , softplus, elu, relu 중에 아무거나 사용한다.
- Posterior Cluster Assignment Probabilites $\phi$는 모든 K에 대해서 계산된다. 상호 배타적인 부분이기 때문에 확률 값으로 부여하기 위해 softmax를 사용한다.
손실 함수를 정의하는 것은 Tensorflow-probability를 사용했다고 한다. (tfp.distributions.MixtureSameFamily)
그러나 만약 손실을 계산하길 원한다면, 아래 형태로도 코드를 짜면 된다고 한다.
## tensorflow probability built-in 사용
self.mixture_distribution = tfp.distributions.Categorical(probs=self.pi)
self.distribution = tfp.distributions.Normal(loc=self.mu, scale=self.var)
self.likelihood = tfp.distributions.MixtureSameFamily(
mixture_distribution=self.mixture_distribution,
components_distribution=self.distribution)
self.log_likelihood = -self.likelihood.log_prob(tf.transpose(y))
self.mean_loss = tf.reduce_mean(self.log_likelihood)
## 안사용한 경우
self.likelihood = tfp.distributions.Normal(loc=self.mu, scale=self.var)
self.out = self.likelihood.prob(y)
self.out = tf.multiply(self.out, self.pi)
self.out = tf.reduce_sum(self.out, 1, keepdims=True)
self.out = -tf.log(self.out + 1e-10)
self.mean_loss = tf.reduce_mean(self.out)손실은 위에서 언급한 GMM Likelihood 식과 같은 방법으로 계산된다.
- 처음에는 각 구성요소마다 $\mu, \sigma$를 계산한다. 그리고 posterior probability($\phi$)를 계산한다.
- $\phi$와 결합된 구성요소를 곱한다. 그리고 likelihood를 얻기 위해서 모든 사후 확률을 더한다.
- 그때 Log Likelihood를 취하고 모든 샘플에 대해서 더한다.
- 그다음에 negative log-likelihood의 평균을 계산한다.
필자는 개인적으로 tensorflow_probability를 잘 사용해보지 않았지만, 앞으로 이러한 확률적인 계산을 할 경우가 많을 것 같으니 공부를 해야겠다고 생각했다.
tfp.distributionsCategorical 는 categorical loss를 정의한다.
정규 분포로 제한할 때, tensorflow-probability를 사용하여 정의할 수 있다.
MixtureSameFamily는 mus 및 sigma의 벡터를 혼합 분포에 대한 공분산 행렬로 변환한다.
그때 negative log-likelihood를 마지막으로 최소화하고 log_likelihood를 출력하기 위해 log-prob을 사용한다.
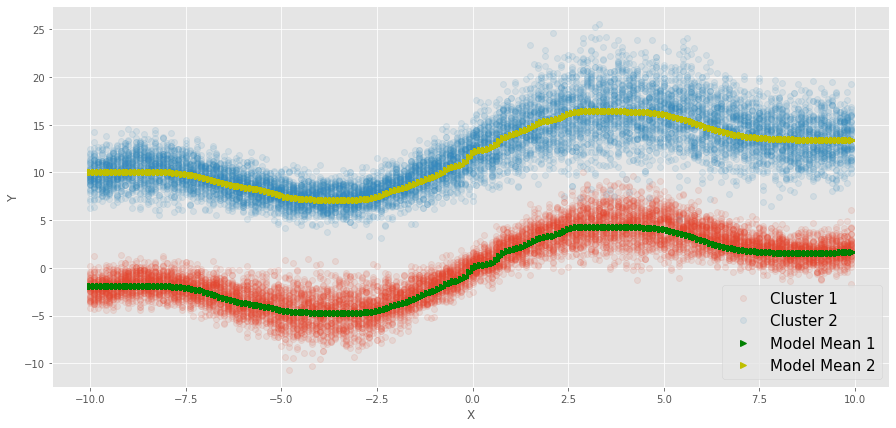
기대했던 대로 2개의 구성요소를 잘 학습한 것을 알 수 있다!!
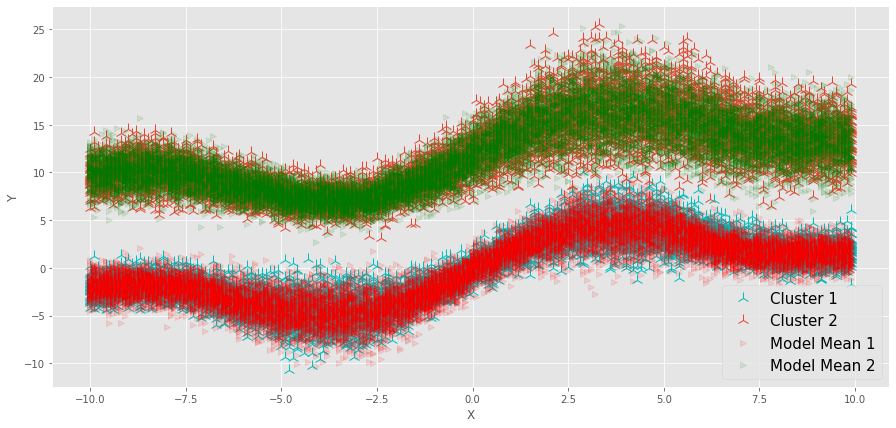
분산을 보기 위해서 랜덤한 샘플을 만들어서 테스트한 것이 오른쪽 그림이다!
MLP 모델과 비교하면 확실히 2개의 뚜렷한 군집을 가지는 것을 알 수 있다.
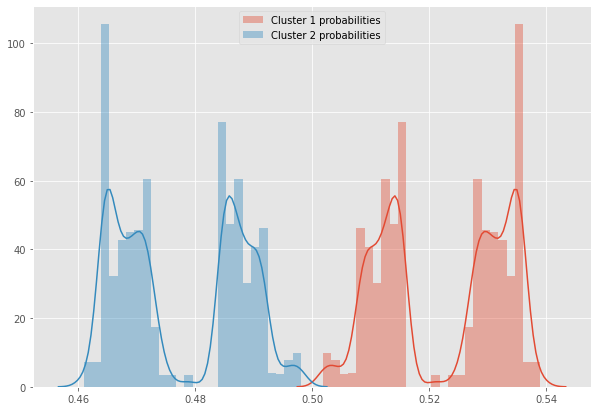
$\phi$에 대해서 softmax를 잘 학습하면 다음과 같다고 한다.
여기서 군집 확률은 거의 50%로 균등하게 비중이 되어 있다. 분산은 46%-54%를 띄고 있다.
실제로 예제를 만들 때 $P(cluster=1|x) ==P(cluster=2|x)$로 했으니, 어느 정도 만족하는 결과일 수도 있다.
결론
MDN 설명과 함께 코드를 볼 수 있어서 참 좋았고, 쉽게 잘 설명된 글이여서 좋았다.
앞으로 MDN을 어떻게 사용할 수 있을지 고민해봐야겠다!
https://towardsdatascience.com/learning-from-multimodal-target-5d3d2ea0d4c5
Learning from Multimodal Target
Mixture Density Neural Network — the violation of assumptions, implementation, analysis, and applications using Tensorflow.
towardsdatascience.com
https://github.com/dwipam/MDN/blob/master/MDN_NOTEBOOK.ipynb
dwipam/MDN
Mixed Density Networks. Contribute to dwipam/MDN development by creating an account on GitHub.
github.com
'분석 Python > Tensorflow' 카테고리의 다른 글
| Mixture Density NeuralNetwork 예제 (0) | 2020.05.21 |
|---|---|
| tf.layers.dense 알아보기 (tf.tensordot ,tf.matmul) (0) | 2020.04.24 |
| tf.py_func 사용해보기 (0) | 2020.04.17 |
| tf.data 삽질해보기 (two iterator, feed_dict, GAN) (0) | 2020.04.08 |
| tf.data로 데이터 파이프라인 만들고 추론하는 것 까지 해보기 (0) | 2020.03.22 |