- 일반적인 GAN에서 Discriminator가 Gradient 가 소실되는 현상이 종종 일어나서 학습이 안되는 경우가 있음.
- 그리고 이러한 GAN을 향상시키기위해 LSGAN, Wasserstein Distance 와 Gradient Penalty를 사용한 WGAN-GP가 나왔고 이러한 GAN들은 Integral probability Metrics를 기반으로한 논문들이 많이 나오게 됨.
- IPM을 기반으로 한 GAN들은 Fake 와 Real을 완벽하게 구분하는 것을 방지함으로써, 학습을 계속했을 때 Gradient가 사라지는 현상 없이 학습을 시킬 수 있음.
Integral Probability Metric(IPM)

- IPM 이란 각 분포의 Expectation 값의 차이를 계산한 값임.
- 그러나 이러한 IPM은 Loss 함수의 발산을 빠르가 발산하는 것을 가정하기 때문에 각 IPM 마다 Discriminator에 다른 제약을 적용하게 됨.
- 그래서 IPM 기반으로 한 GAN들(LSGAN , WGAN-GP)은 실제로 Metric 과 Divergence 에 안정성에 대한 설명을 할 수가 없고, 그래서 이 논문은 non-IPM 을 기반으로 한다고 함.
- 이 논문에서는 발산을 최소로 하는 GAN을 만들면서, Batch 크기 안에서 절반은 Fake를 사전 지식을 기반으로 해서 더 나은 예측을 하는 GAN을 만들려고 하는게 주장함.
- Prior Knowledge
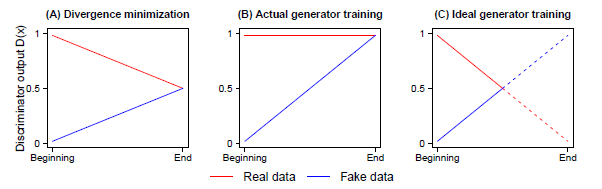
- 일반적인 GAN에서의 Discriminator가 최적으로 수렴시, (A)와 같이

- 이 될거라는 것이 증명되지만, 실제로 우리가 원하는 학습은 (C)와 같이 학습 중간에
 와 같이 진행되는 것을 원함.
와 같이 진행되는 것을 원함.
- 하지만 실제로 학습시 모든 샘플에 대해서 진짜라고 판단하기 때문에 위에 나와 있는 (B) 와 같이 D(x) = 1 같은 형태로 학습을 하게 됨.
- 이처럼 일반적인 GAN은 Batch 크기에서 절반은 가짜라는 사전지식을 무시하게 됨.
- Divergence minimization argument
- 실제로 최적의 the Jensen–Shannon divergence 구하면 다음과 같음.
- 하지만 우리가 실제로 학습시
 이 아닌 1로 가게 되고
이 아닌 1로 가게 되고  이 아닌 1로 가게 됨.
이 아닌 1로 가게 됨.
- $D(X_r) \quad : \quad \frac{1}{2} -> 1 \qquad D(X_f) \quad : \quad \frac{1}{2} -> 1$
- 이런식으로 학습을 하다 보니 JSD 가 최적으로 가지 못합니다. 그래서 실제로 JSD 의 최적값을 구하기 위해서
-
- $D(x_r)$은 감소하면서 $D(x_f) \frac{1}{2}$ 까지 증가하는 형태로 되야함.
제시하는 방법론

- 일반적인 GAN의 Discriminator는 파랑색 줄과 같은데, 이 논문에서 주장하는 방법은 빨간 줄과 같음.
- 논문에서는 사전지식을 바탕으로 한 값을 주기 위해 real 에서 fake의 Layer 값을 뺀 다음에 sigmoid를 주는 식임.
- $sigmoid( C(x_r) - C(x_f))$
- 해석은 랜덤하게 샘플링 된 fake 데이터 보다 주어진 real data가 더 실제일 확률이라 할 수 있음.
- $D_{rev}(\tilde x) = sigmoid( C(x_f) - C(x_r))$
- 실제 샘플링 된 데이터 보다 fake 데이터가 더 진짜일 확률로 해석 할 수 있음.
- 위에 Loss를 해석
- Discriminator : $$sigmoid( C(x_r) - C(x_f))$$ 는 1에 가깝게 함으로써, Real Data 와 Fake Data를 잘 구별하게 하는 것이 목표임.
- Generator : $$sigmoid( C(x_f) - C(x_r))$$ 는 1에 가깝게 함으로써 Fake Data 가 주어진 데이터보다 더 Real 같은 확률을 만들게 함
- 두 Loss방식을 Adversarial 하게 함으로써 학습을 하게 함.
RSGAN-GP
$L_D^{RSGAN GP} = - E_{X_r ,X_f}( log( sigmoid( C(X_r) - C(X_f)))) + \lambda E( \lVert \bigtriangledown_{X_r, X_f}( D(X_r, X_f)\rVert - 1)^2$
$L_G^{RSGAN GP} = - E_{X_r ,X_f}( log( sigmoid( C(X_f) - C(X_r))))$
- 실제로 사용한 Loss는 현재 IPM에서 잘 학습이 된다고 알려진 WGAN GP와 결합하여 사용하였음.
- 그리고 이 논문에서도 사용하고, 요즘 많이 사용하는 Weight를 Normalize 해주는 Spectral Norm 도 같이 사용하였음.
- 또한 Gradient Penalty 을 사용함으로써, 좀 더 확실하게 Weight 가 튀지 않게 방지하게 하였습니다.
Gradient Penalty
- 이전에 IPM 계열에서 학습이 계속 안정되게 한 역할을 한 Gradient Penalty도 Discriminator Loss Function에 추가함으로써, Gradient 소실을 방지하게 함.
- Penalty 만을 주는 것은 Gradient 자체 값이 크게 튀지 않는 것만 방지하기 때문에 논문에서도 나오듯이 Spectral Norm을 사용해서, Gradient의 Normalize 함으로써 학습동안에 소실되는 것을 막음.
- 실험 중에 다음과 같은 예제가 있다.
- $C(x_r) - C(x_f) = 13 $
- $sigmoid(13) = 1 = P( x_r \quad is \quad bread | C(x_f)$
- $C(x_r) = 8 $
- $sigmoid(8) = 1 = P( x_r \quad is \quad bread )$
- 이 예제에서는 판별식이 기존 Loss랑 새롭게 제안한 Loss 에서 둘 다 빵이라고 할 확률을 1로 나타낸다
정리 및 나의 생각
일반적인 GAN Loss나 WGAN 계열인 IPM 계열에서 먼가 느슨한 Loss를 주는 것 같아 개인적으로 아쉬웠는데,
해당논문에서 Prior를 고려하는 즉 진짜 샘플과 가짜 샘플은 항상 반반식 있다는 것을 가미해서 쓴 Loss가 좀 더 합리적이게 느껴진다.