728x90
전제를 두고 한다.
- lambda 는 lassocv를 이용해서 지정한다.
- tolerance 를 줘서 loop를 빠져나가게 한다.
- x와 y 는 임의로 줬다고 하자
그다음에 soft-thresholding에 다른 모습을 이용해서 coordinate Descent 하는 것을 보이겠다.
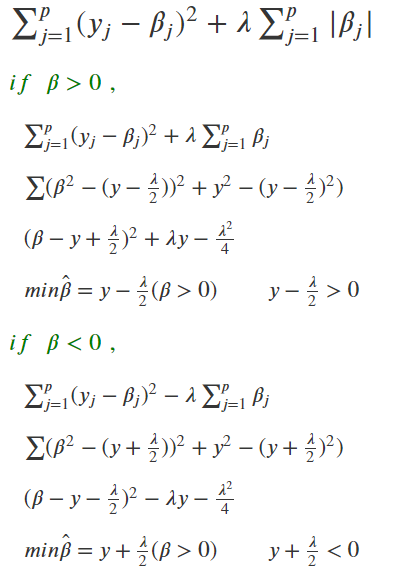

다음 과 같이 정리할 수 있다. 구체적인 식은 나중에 잘 써서 올리겠다.
결국 오른쪽의 하단의 식을 계속 업데이트 해나가면서, 점점 최적화를 진행하면 된다.
np.random.seed(19510)
reg = LassoCV(cv=5, random_state=0).fit(train_x , train_y )
best_alpha = reg.alpha_
x_corr = pd.DataFrame(train_x).corr().values
print("Best Alpha : {}".format(best_alpha))
print("coefficient : {}".format(reg.coef_))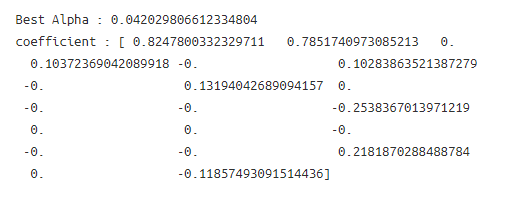
## init 값
np.set_printoptions(precision= 10000)
from scipy.spatial.distance import euclidean
coef = np.random.uniform(1,2,20)
x_corr = pd.DataFrame(train_x).corr().values
rang = np.arange(20)
## tolerance
tol = 1e-300
## 1000번 해도 못 나올 시 빠져나오게 하기
max_num = 1000
num = 0
dist_list = []
while True :
pre_coef = np.copy(coef)
coef = np.copy(coef)
for idx in rang :
select_x = train_x[:,idx]
r_xy = np.corrcoef(select_x , np.squeeze(train_y))[0,1]
select_xx = np.where(rang != idx )[0]
r_xx = np.sum(x_corr[idx,:][select_xx] * coef[select_xx])
t = r_xy - r_xx
term = np.abs(t) - best_alpha/2
term = term if term > 0 else 0
coef[idx] = np.sign(t)*term
dist = euclidean(pre_coef , coef)
if (dist < tol) | (num > max_num) :
print("Iteration : {} ,".format(num) )
print("Dist : ", dist)
print("Gradient Descent : \n {} ".format(coef) )
break
else :
num += 1
dist_list.append(dist)
coef = np.copy(coef)
print("Best coefficient : \n {}".format(reg.coef_))

주의! Gradient가 아니라 Coordinate입니다!
끝
'분석 Python > Scikit Learn (싸이킷런)' 카테고리의 다른 글
| sklearn Pipeline을 이용해 다양한 Regression모델 모델링하기 (0) | 2019.06.15 |
|---|---|
| sklearn Pipeline을 이용해 다양한 Classification모델들 모델링하기 (0) | 2019.06.15 |
| Sklearn SVM + OneVsRestClassifer Gridsearch (0) | 2019.06.15 |
| [ Python ] Scikit-Learn, Numeric 표준화 / Category Onehot 하는 Pipeline 및 모델링하는 코드 (0) | 2019.06.15 |
| Ridge, Lasso, ElasticNet / train, test, coef 값 내뱉는 multiprocessing 함수 만들기 (0) | 2019.05.06 |