- 정형데이터 AI 모델 개발 방식
- 정형데이터 AI 모델 개발 방식 트렌드
- 개인적인 생각 (정형데이터에서 트리가 더 잘 되는 이유)
- 범주형 변수
- 실습 코드(Python)
- 범주형) 원-핫 인코딩 (One-Hot Encoding)
- 범주형) 밀도 인코딩 (Target Encoding 또는 Mean Encoding)
- 범주형) 이진 인코딩 (Binary Encoding)
- 범주형) 임베딩 (Embedding) - torch
- 연속형) Linear Embeddings - torch
- 연속형) Linear Embeddings - FT-Transformer
- 연속형) Piecewise Linear Encoding (Quantile Binning)
- 연속형) Piecewise Linear Encoding (Target Binning Approach)
- 결론
- 참고자료
2023. 10. 4. 23:55ㆍ분석 Python/구현 및 자료

정형 데이터를 딥러닝에 사용할 때 임베딩하는 방법에 대해서 정리해보고자 한다.
흔히 아는 머신러닝과 딥러닝의 차이를 이런 식으로 표현한다.
(물론 딥러닝은 머신러닝의 부분집합이긴 해서 이렇게 구분하는 게 맞지는 않기는 한 것 같다)
여기서 말하는 머신 러닝은 흔히 이야기하는 tree 계열 알고리즘이나 회귀분석 같은 통계 기반의 방법론들을 생각해 주면 될 것 같다.
정형데이터 AI 모델 개발 방식
말하고자 하는 것은 흔히 딥러닝을 써서 얻을 수 있는 기대효과는 알아서 데이터에 대한 정보를 추출(feature extraction)할 수 있다는 믿음하에 딥러닝 방법론을 많이 사용하게 된다.

정형데이터 AI 모델 개발 방식 트렌드
크게 현재 데이터로 많이 사용하는 것이 tabular, image, text, graph, audio... 등등 많은 것들이 있고, image, text, graph, audio 같은 것에서는 딥러닝으로 좋은 모델 성능이 나오는 사례가 많다.
하지만 tabular 같은 부분에 대해서는 아직도 전통적인 통계 방법론들과 비교했을 때 딥러닝이 항상 좋다는 결과는 나오지 않고 있다.
이게 공식적인 자료인지는 모르겠으나, 아직까지도 많은 Kaggle 대회에서는 scikit-learn을 사용하고 있고,
tabular 데이터만 뽑고 나서 알고리즘을 비교해본다면, scikit-learn 사용을 더 많이 할 것이다.

(https://twitter.com/fchollet/status/1580252953809948673/photo/1)
그래서 현재 딥러닝 관련 논문에서는 통계적인 방식을 딥러닝으로 구현한 논문들도 나오고 있는 상황이다.
(https://arxiv.org/abs/1711.09784)
(https://arxiv.org/abs/1908.07442)
그렇다면, 왜 정형데이터에서 딥러닝보다 통계적인 방법이 더 성능이 좋게 나오는 걸까에 대해서 궁금해졌고,
대략적으로 먼가 다들 추정이지만, 공감하는 것들이 있었다.
개인적인 생각 (정형데이터에서 트리가 더 잘 되는 이유)
일반적으로 tree 방식 같은 경우, 데이터에 대해서 메트릭을 기준을 분기처리를 통해서, 각각의 데이터를 그룹화하고, 그 그룹에 대해서 라벨을 부여하는 방식으로 데이터가 학습하게 된다.

즉 각 피처마다 메트릭 기준으로 중요도를 찾아서 데이터를 분류시키기는 방법으로 모델링을 하게 된다.
그래서 중요한 피처 한개만 있으면, 데이터를 쉽게 분류할 수 있게 된다.
그렇다면 딥러닝은 보통 어떻게 되는지 대략적으로 그림으로 보면 다음과 같다.
이런 식으로 특정 뉴런들이 있고, 그 뉴런들이 데이터(주황색)와 가중합을 통해서, 예측 결과를 내는 형식이다.
이러한 방식은 모든 뉴런들이 다른 피처들과의 가중합을 통해서, 이상치나 아니면 특정 값에 대해서 예민하게 되는 모델 구조라고 볼 수 있다.

또 하나로 생각이 되는 점은 데이터의 분포가 다 다르다는 것이다.
일반적으로 비정형데이터 중에서 이미지를 예시로 들면 각각의 픽셀은 (0~255)로 되어있고, 각각의 가지는 의미가 동일하다. 하지만 정형데이터 같은 경우, 일단 범주형 변수, 연속형 변수 같이 데이터 타입이 다르기도 하고, 각각의 피처마다 가지는 값 자체가 가지는 의미가 다르다는 것이다.
물론 이러한 것들 때문에 데이터 전처리를 통해 스케일을 일치시켜주는 작업을 하긴 하지만, 의미가 다른 것들끼리 가중합을 가지기 때문에 문제가 될 수 있다.
여기서 개인적으로 딥러닝이 통계적인 머신 러닝 방법론들보다 못한 점에 대한 간단한 나의 생각이고, 결국에 중요한 것은 데이터를 어떻게 잘 딥러닝이 학습할 수 있게 표현하는지가 중요하다는 것이다.
현재 딥러닝은 대세가 되고 있고, 여러 데이터를 결합해서 모델링하는 것이 중요해지는 시대인 만큼, 딥러닝으로 정형데이터를 잘할 수 있는 방법에 대해서 생각해봐야한다.
즉, 결국 기존에 가진 데이터를 어떻게 모델이 잘 학습할 수 있게 잘 표현하는 것이 중요하다.
보통 이런 것을 피처를 잘 뽑아낸다고 하는데, 여기서는 결국 딥러닝은 연속형 데이터를 처리하는 거기 때면에 연속적인 벡터 공간으로 맵핑하는 작업이 잘 돼야 한다.
정형 데이터 같은 경우, 딥러닝에 넣기 전에 2가지 방법으로 흔히 할 수 있다.
1. 범주형 데이터를 인코딩해서, 숫자화 시켜서 연속형 변수와 같이 딥러닝 네트워크에 적용
2. 연속형 데이터를 네트워크에 태우고, 범주형 데이터를 임베딩해서 숫자화시키고 네트워크에 태운 다음에 붙이는 작업
범주형 변수
특히 범주형 변수가 정형데이터에서만 나올 수 있는 특이한 경우라고 볼 수 있다.
위에서 보면 임베딩이랑 인코딩이란 표현이 나오는데,
범주형 변수의 인코딩:
범주형 데이터를 수치형 데이터로 변환하는 과정을 의미한다.
대부분의 머신러닝 알고리즘은 수치형 입력을 필요로 하기 때문에, 범주형 변수를 적절한 수치형 형태로 변환하는 것
범주형 변수의 임베딩:
범주형 변수는 특정한 범주 또는 클래스로 값을 가지는 변수. 예를 들어, '색상' 변수는 '빨강', '파랑', '녹색' 등의 범주 값을 가질 수 있다. 이러한 범주형 변수를 그대로 딥러닝 모델에 입력으로 사용하는 것은 비효율적이다.
따라서 범주형 변수의 각 범주 값을 저 차원의 연속적인 벡터로 변환하는 임베딩 과정이 필요하다.
정형 데이터에서 임베딩의 장점:
의미적 표현: 임베딩을 통해 유사한 범주 값들은 임베딩 공간에서 서로 가까이 위치하게 된다. 이는 모델이 범주 간의 관계를 더 잘 이해하도록 도와준다.
차원 축소: 범주형 변수에 많은 고유한 범주가 있을 경우, 원-핫 인코딩과 같은 전통적인 방법은 매우 큰 차원의 벡터를 생성한다. 임베딩을 사용하면 이러한 변수를 훨씬 작은 차원의 벡터로 표현할 수 있다.
모델 성능 향상: 임베딩을 통해 범주형 변수의 정보를 더 효과적으로 표현할 수 있으므로, 딥러닝 모델의 성능이 향상될 수 있다.
예시:
고객 데이터에서 '직업'이라는 범주형 변수가 있을 때, '의사', '변호사', '선생님' 등의 여러 직업 범주가 있을 수 있습니다. 이러한 범주를 원-핫 인코딩으로 표현하면 각 직업마다 하나의 차원이 필요합니다. 반면, 임베딩을 사용하면 각 직업을 예를 들어 5차원의 벡터로 표현할 수 있습니다. 이렇게 변환된 벡터는 딥러닝 모델의 입력으로 사용될 수 있습니다.
개인적으로 정형데이터에 딥러닝을 모델링한다고 할 때 코드가 복잡해지지만, 임베딩을 하는 것을 선호하는 편이다.
방법론 (chatgpt)
원-핫 인코딩 (One-Hot Encoding):
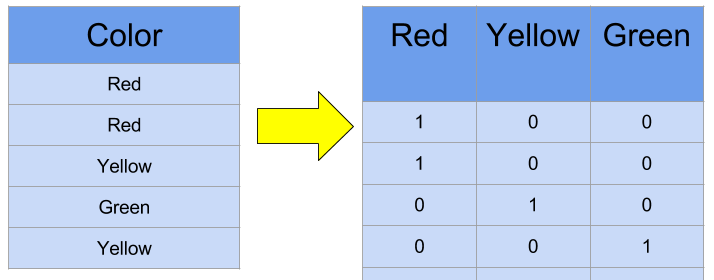
각 범주를 독립적인 이진 변수 (0 또는 1)로 변환합니다.
예: 색상 변수가 "빨강", "파랑", "녹색"의 세 가지 범주를 가질 때, 원-핫 인코딩을 사용하면 각 색상은 다음과 같이 표현됩니다:
빨강: [1, 0, 0]
파랑: [0, 1, 0]
녹색: [0, 0, 1]
순서 인코딩 (Ordinal Encoding):
범주에 순서를 부여하여 정수로 변환합니다.
예: 사이즈 변수가 "소", "중", "대"의 세 가지 범주를 가질 때, 순서 인코딩을 사용하면 다음과 같이 표현됩니다:
소: 1
중: 2
대: 3
밀도 인코딩 (Target Encoding 또는 Mean Encoding):
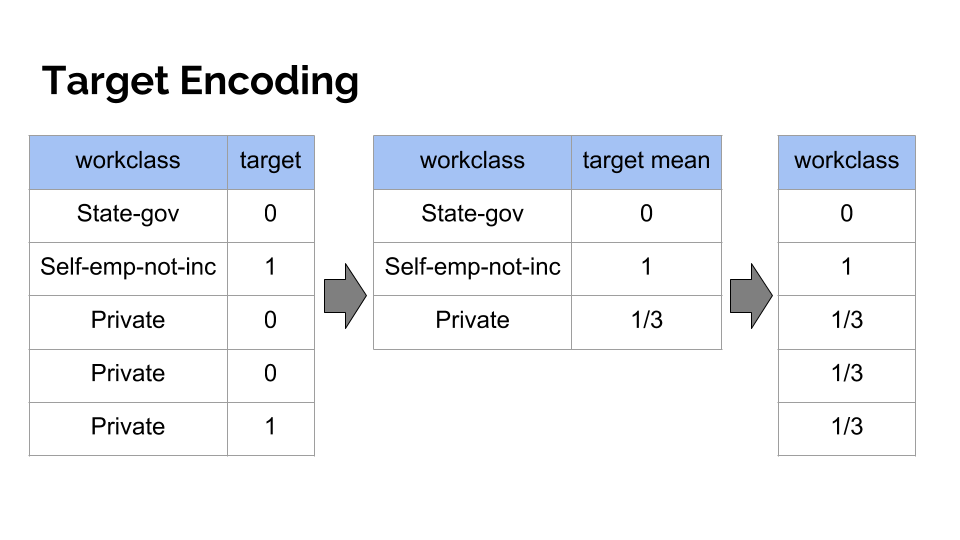
각 범주의 값을 해당 범주의 타겟 변수의 평균값으로 변환합니다.
주로 분류 문제에서 사용되며, 과적합의 위험이 있어 교차 검증을 통한 정규화가 필요할 수 있습니다.
이진 인코딩 (Binary Encoding):
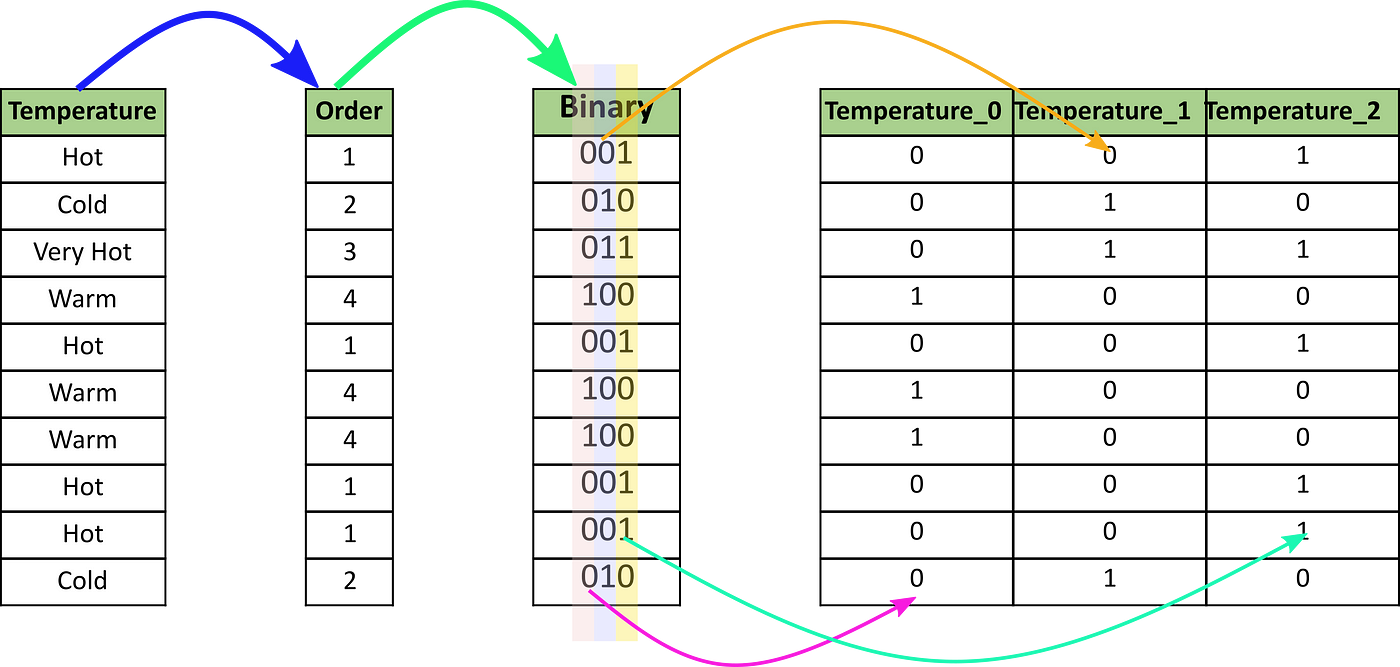
범주를 순서 인코딩으로 변환한 후, 이진 코드로 변환합니다.
원-핫 인코딩보다 적은 차원으로 범주를 표현할 수 있습니다.
임베딩 (Embedding):
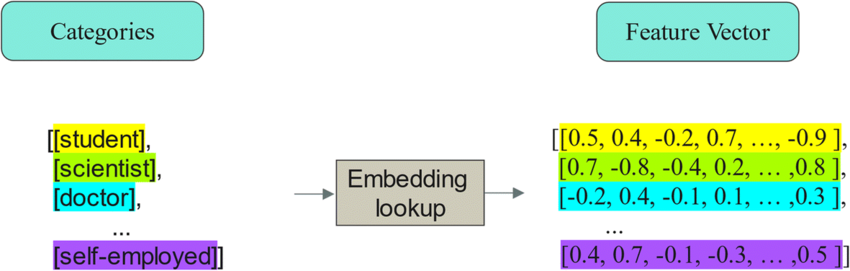
딥러닝에서 사용되는 방법으로, 각 범주를 저차원의 연속적인 벡터로 변환합니다.
임베딩 레이어를 통해 학습되며, 범주 간의 복잡한 관계를 포착할 수 있습니다.
Linear Embeddings
수치 임베딩 레이어는 단일 실수를 밀집된 수치 표현(임베딩)으로 변환합니다. 이러한 변환은 유용하다고 볼 수 있는데, 이러한 임베딩 들은 범주형 임베딩과 함께 트랜스포머 블록을 통과할 수 있기 때문입니다. 이로 인해 더 많은 컨텍스트에서 학습할 수 있게 됩니다.

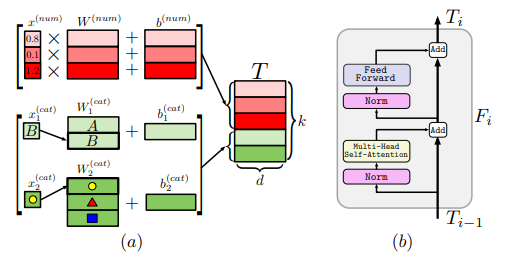
Linear Embeddings - FT-Transformer
(Feature Tokenizer Transformer 방식)
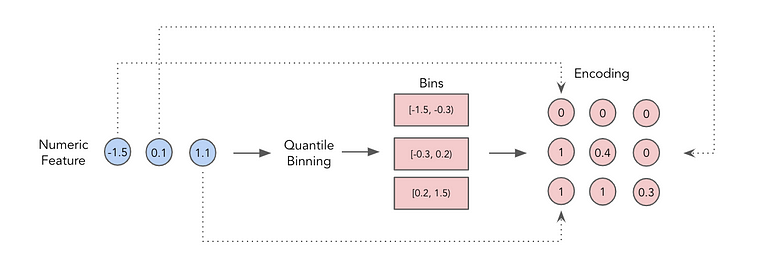
Piecewise Linear Encoding (Quantile Binning Approach)

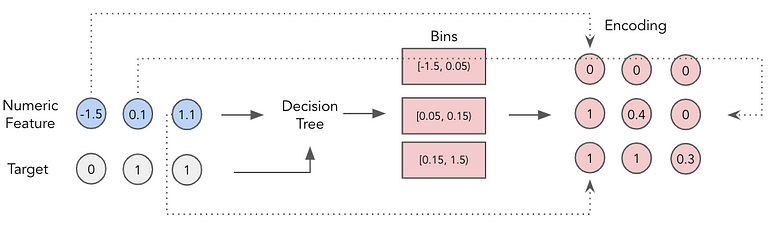
Piecewise Linear Encoding (Target Binning Approach)
그래서 이번 글에서는 정형데이터를 딥러닝에 활용할 때 자주 사용할 수 있는 방법에 대해서 정리해보고자 한다.
|
|
실습 코드(Python)
범주형) 원-핫 인코딩 (One-Hot Encoding)
import pandas as pd
# 범주형 데이터를 담은 데이터프레임 생성
data = pd.DataFrame({'Animal': ['cat', 'dog', 'bird', 'fish']})
# Pandas의 get_dummies 함수를 사용하여 원-핫 인코딩 수행
one_hot_encoded = pd.get_dummies(data, columns=['Animal'])
print(one_hot_encoded)
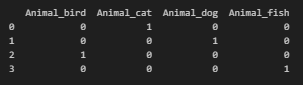
범주형) 밀도 인코딩 (Target Encoding 또는 Mean Encoding)
Target - Regression
import pandas as pd
# 샘플 데이터 생성
data = pd.DataFrame({
'Category': ['A', 'B', 'A', 'C', 'B', 'C'],
'Target': [10, 20, 15, 25, 30, 35]
})
# 각 범주(Category)의 평균 타겟 값으로 대체
target_mean = data.groupby('Category')['Target'].mean()
data['Target_Encoded'] = data['Category'].map(target_mean)
print(data)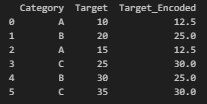
Target - Binary
import pandas as pd
# 샘플 데이터 생성
data = pd.DataFrame({
'Category': ['A', 'B', 'A', 'B', 'A', 'A'],
'Target': [1, 0, 1, 1, 0, 1]
})
# 이진 분류에서의 Target Encoding
target_encoded = data.groupby('Category')['Target'].mean()
data['Target_Encoded'] = data['Category'].map(target_encoded)
print(data)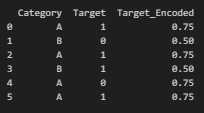
범주형) 이진 인코딩 (Binary Encoding)
조금 다른 형태이긴 하지만 category_encoders 라이브러리를 활용해서, 이진 맵핑
import pandas as pd
import category_encoders as ce
# 샘플 데이터 생성
data = pd.DataFrame({
'Category': ['A', 'B', 'A', 'B', 'C']
})
# Binary Encoding 수행
binary_encoder = ce.BinaryEncoder(cols=['Category'])
binary_encoded_data = binary_encoder.fit_transform(data)
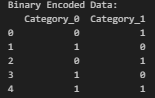
print(data)
print("Binary Encoded Data:")
print(binary_encoded_data)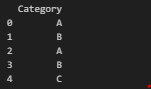
범주형) 임베딩 (Embedding) - torch
범주형 같은 경우, 문자를 숫자로 변환하는 작업이 우선 필요하고, 각각의 값을 인덱스로 맵핑하는 작업이 필요하지만, 이 부분은 생략
import pandas as pd
import numpy as np
import torch
from torch import nn
# 샘플 데이터 생성
data = pd.DataFrame({
'Category_1': ['A', 'B', 'A', 'B', 'C'],
'Category_2': ['X', 'Y', 'X', 'Z', 'Z']
})
# 범주형 변수를 고유한 숫자로 매핑
data['Category_1_Encoded'] = data['Category_1'].astype('category').cat.codes
data['Category_2_Encoded'] = data['Category_2'].astype('category').cat.codes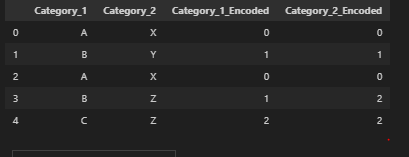
# 각 범주형 변수의 임베딩 차원 설정
embedding_dim_1 = 3
embedding_dim_2 = 2
# 임베딩 레이어 생성
embedding_layer_1 = nn.Embedding(len(data['Category_1_Encoded'].unique()), embedding_dim_1)
embedding_layer_2 = nn.Embedding(len(data['Category_2_Encoded'].unique()), embedding_dim_2)
# 임베딩 레이어에 입력할 데이터
categorical_data_1 = torch.LongTensor(data['Category_1_Encoded'].values)
categorical_data_2 = torch.LongTensor(data['Category_2_Encoded'].values)
# 임베딩 적용
embedded_data_1 = embedding_layer_1(categorical_data_1)
embedded_data_2 = embedding_layer_2(categorical_data_2)
print("Embedded Data (Categorical Variable 1):")
print(embedded_data_1)
print("\nEmbedded Data (Categorical Variable 2):")
print(embedded_data_2)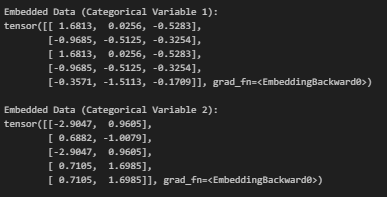
연속형) Linear Embeddings - torch
linear embedding으로 단일 실 수 값에 weight를 곱하고, 추가적으로 카테고리마다 embedding을 통해 bias를 넣어주는 식으로 해서 구별을 두는 식으로 구현해 봄.
import torch
import torch.nn as nn
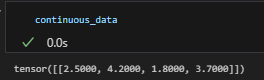
# 샘플 연속형 데이터
continuous_data = torch.Tensor([2.5, 4.2, 1.8, 3.7]).reshape(1,-1)
bs, cont_dim = continuous_data.size()
# Linear Embedding을 적용할 때 사용할 가중치 행렬 설정
embedding_dim = 10 # 임베딩 차원
embedding_layer = nn.Linear(1, embedding_dim) # 입력 차원은 1 (스칼라), 출력 차원은 임베딩 차원
embedding_cont_layer = nn.Embedding(cont_dim+1,embedding_dim=embedding_dim)
embedding_linear_bias = embedding_cont_layer(torch.ones_like(continuous_data).cumsum(axis=1).long())
# 연속형 데이터를 범주형 데이터로 변환 (예: 정수화)
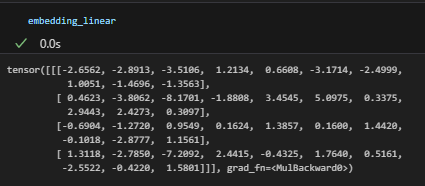
embedding_linear = embedding_layer(continuous_data.unsqueeze(-1))
embedding_linear = embedding_linear + embedding_linear_bias
print(embedding_linear.size(),embedding_linear_bias.size(),embedding_linear.size())연속형) Linear Embeddings - FT-Transformer
간단하게 설명하면, 연속형 변수 postion에 대한 embedding 벡터를 구한 후, 그 벡터의 가중치를 연속형 값을 넣어서 스케일을 결정하는 코드로 이해함. (bias는 제외함)
import torch
import torch.nn as nn
# 샘플 연속형 데이터
continuous_data = torch.Tensor([2.5, 4.2, 1.8, 3.7]).reshape(1,-1)
bs, cont_dim = continuous_data.size()
# Linear Embedding을 적용할 때 사용할 가중치 행렬 설정
embedding_dim = 10 # 임베딩 차원
embedding_cont_layer = nn.Embedding(cont_dim+1,embedding_dim=embedding_dim)
embedding_linear_numerc_col = embedding_cont_layer(torch.ones_like(continuous_data).cumsum(axis=1).long())
embedding_linear = continuous_data.unsqueeze(-1) * embedding_linear_numerc_col
print(embedding_linear.size(),embedding_linear_numerc_col.size())
연속형) Piecewise Linear Encoding (Quantile Binning)
numpy로 PLE를 구현하면 다음과 같음
0에서 1까지를 5 등분해서 진행함.
def array_to_32bit(x):
return np.array(x, dtype=np.float32)
def map_to_bins(x, b):
x = array_to_32bit(x)
T = len(b) - 1
batch_size, feature_dim = x.shape
t_values = np.arange(1, T + 1).reshape(1, 1, T) # Shape: (1, 1, T)
x_expanded = x[:, :, np.newaxis] # Shape: (batch_size, feature_dim, 1)
b_expanded = b[np.newaxis, np.newaxis, :] # Shape: (1, 1, T+1)
condition_1 = (x_expanded < b_expanded[:, :, :-1]) & (t_values > 1)
condition_2 = (x_expanded >= b_expanded[:, :, 1:]) & (t_values < T)
result = np.where(
condition_1,
0,
np.where(
condition_2, 1, (x_expanded - b_expanded[:, :, :-1]) / (b_expanded[:, :, 1:] - b_expanded[:, :, :-1])
),
)
return result
import numpy as np
bs = 1
feat_dim = 4
data = np.random.rand(bs,feat_dim)
print(data)
b = np.linspace(0,1,5)
print(map_to_bins(data,b))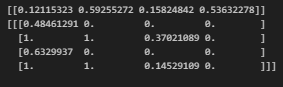
연속형) Piecewise Linear Encoding (Target Binning Approach)
위의 quantile binning 같은 경우, 균등하게 데이터를 나누기 때문에 target에 대한 인코딩이 잘 안될 수도 있다는 가정하에서 binning 을 target 기반으로 하는 방식에 대해서 소개하고자 한다.
해당 방식은 특정 연속형 변수와 특정 타겟간의 관계를 학습시킨 후 분기점을 bin 방식으로 활용하는 방식이다.
해당 방식을 통해 특정 데이터간의 분기점을 잘 파악할 수 있어서, overfitting에 위험도 있을 수 있지만, 데이터 패턴을 잘 나눌 수 있을 것 같기도 하다.
import numpy as np
from sklearn.tree import DecisionTreeClassifier
# 대량의 샘플 연속형 데이터 생성
np.random.seed(42)
continuous_data = np.random.rand(100) * 20 # 0에서 10 사이의 연속형 데이터
continuous_data = continuous_data.reshape(-1, 1)
# 대량의 Target 데이터 생성 (이진 형태, 예시로 0 또는 1)
target_data = np.random.randint(0, 2, size=100)
# 구간(bin)의 개수 설정
num_bins = 5
# Decision Tree Classifier를 사용하여 구간 결정
tree_classifier = DecisionTreeClassifier(max_leaf_nodes=num_bins)
tree_classifier.fit(continuous_data, target_data)
bins = np.sort(np.unique(tree_classifier.tree_.threshold))
print(bins)
## [-2. 15.6030879 17.53388882 18.61373138 19.39494514]print(continuous_data[0:4,:])
print(map_to_bins(continuous_data[0:4,:],bins))
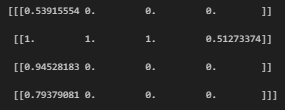
결론
오랜만에 전처리에 대해서 다시 생각해보는 시간을 가지게 되었고, 예전보다는 다양한 방식이 나온 것 같다.
특히 Linear Embedding이나, PLE 같은 방식들은 잘 써보지 않았는데, 데이터 스케일을 처리하는 문제에서나 성능 면에서나 도움이 될 것 같다는 생각이 든다.
해당 방식 이외에도 사실 다양한 방식이 있지만, 위의 방식들을 소개하고 싶어, 여기까지만 작성을 하려고 한다.
추후에 관심이 가는 방식이 있다면 추가할 예정이다.
끝
참고자료
Transformers for Tabular Data (Part 3) : Piecewise Linear & Periodic Encodings
Learn how to apply advanced numerical embeddings to get better deep learning performance for tabular data
towardsdatascience.com
https://github.com/aruberts/TabTransformerTF/blob/main/tabtransformertf/models/embeddings.py
'분석 Python > 구현 및 자료' 카테고리의 다른 글
| Python) AVLTree Search를 통해서 특정 값의 범위 찾기 (ChatGPT와 함께) (0) | 2023.03.22 |
|---|---|
| git) submodule 다루기 (0) | 2023.02.15 |
| python) metaflow 파이썬 스크립트에서 실행해보기 (0) | 2023.02.10 |
| Python) multiprocessing 코어 수 제한해서 돌리기 (0) | 2023.02.04 |
| Python) pyarrow 사용 방법 (0) | 2022.12.21 |
데이터분석뉴비님의
글이 좋았다면 응원을 보내주세요!