우연히 찾은 컴퓨터 알고리즘 강의인데, 출퇴근길에 들어보고 있다.
자료 구조 중의 하나인 Heap에 대해 알아보고 구현하는 것까지 해보려고 한다.
일단 Heap을 사용하는 이유부터 알아보자
Heap은 Prioirty Queue와 같이 우선순위가 존재하는 자료 구조이다.
Heap(힙)이란?
완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조이다.
여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조
- 완전 이진 트리(complete binary tree)에 가까운 형태
- 이진트리(Binary tree)는 각 노드의 자식수가 2 이하인 경우
- 완전 이진 트리는 Root 노드부터 Leaf 노드까지 빠짐없이 채워져 있는 트리

종류
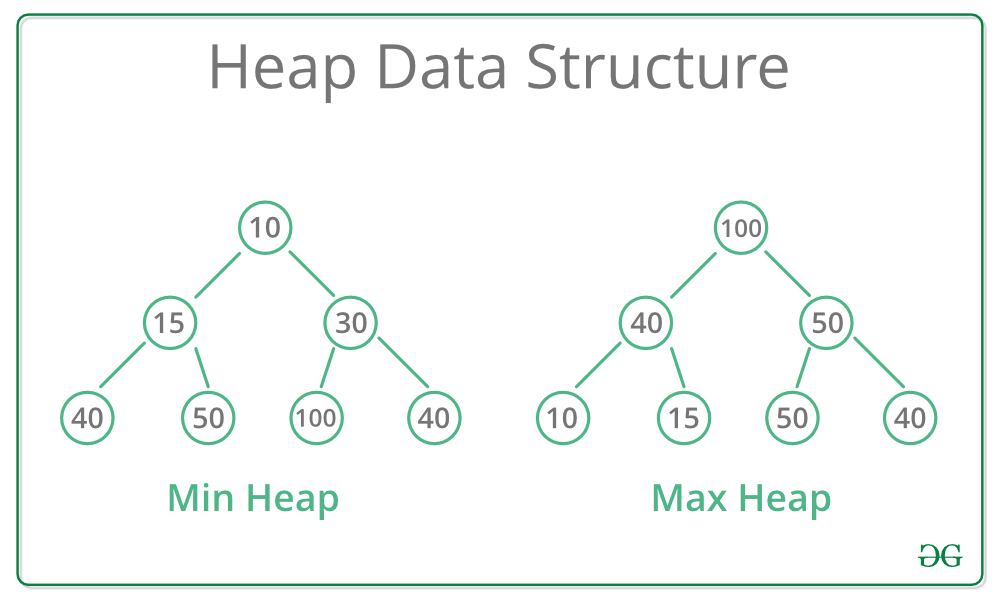
- 최대힙 (max-heap property)
- 부모 노드의 키값이 자식 노드의 키값보다 크거나 같은 완전 이진트리
- 최소 힙 (min-heap property)
- 부모 노드의 키값이 자식 노드의 키값보다 작거나 같은 이진트리


Heap과 Binary Search Tree의 차이
- 둘 다 이진트리
- Binary Search Tree는 왼쪽 자식 노드, 부모 노드, 오른쪽 자식 노드의 순으로 크기가 크지만 Heap은 순서가 없습니다.
- Binary Search Tree는 탐색용 자료 구조 / Heap는 최대 최소 검색을 위한 자료 구조

힙 구조
실제 우리가 생각하는 트리는 왼쪽이고, 실제 구현을 할 때는 array에 다음과 같이 표현한다고 함
아래 예시는 max-heap을 기준으로 표현됨
- root 노드의 배열의 첫 번째 A [1]에 저장
- 각각의 노드들은 레벨별로 저장



검색 기능 가능
- PARENT(i)
- i/2
- LEFT(i)
- 2i
- Right(i)
- 2i+1
예시
parent(4) : 4/2 -> 2
left(4) : 2*4
right(4) : 2*4 +1
이진트리 구조를 가지고 있기 때문에 이러한 기능이 가능
노드의 높이(Height of Node)
노드의 높이는 현재 노드에서 leaf 노드까지 내려갈 때 가장 단순하게 내려가는 가장 긴 경로에서 (simple path) 거쳐야 하는 간선의 수
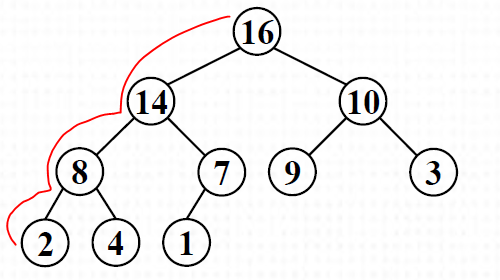
힙의 높이
root 노드로부터 트리의 높이
O(log(n))
- 왜?
- heap은 완전 이진트리 구조를 가지기 때문에 각 레벨마다 노드의 수가 2배씩 증가하므로 O(log(n))
힙 특성 관리(max-heap 기준)
max-heapify
노드가 입력으로 주어졌을 때 노드의 좌 우 하위 트리들은 max-heap 특성을 유지하지만, 노드의 값이 하위 트리 값보다 작거나 같아서 max-heap 특성을 만족하지 않을 때 max-heap 특성이 유지되도록 바꾸는 연산
주어진 노드의 값을 흘러내리게 해서 주어진 노드와 하위 트리가 max-heap 특성을 가질 수 있도록 변경

구현
max-heap을 구현할 때 필요한 연산은 크게 3개가 있음
| Operation | Desc | Time Complexity |
| getMax() | It returns the root element of Max Heap. | O(1) |
| extractMax() | Removes the maximum element from MaxHeap. | O(Log N) |
| insert() | Inserting a new key takes O(Log n) time. We add a new key at the end of the tree. If new key is smaller than its parent, then we don’t need to do anything. Otherwise, we need to traverse up to fix the violated heap property. | O(Log N) |
import sys
class MaxHeap:
def __init__(self, maxsize):
self.maxsize = maxsize
self.size = 0
self.Heap = [0] * (self.maxsize + 1)
self.Heap[0] = sys.maxsize
self.FRONT = 1
# Function to return the position of
# parent for the node currently
# at pos
def parent(self, pos):
return pos // 2
# Function to return the position of
# the left child for the node currently
# at pos
def leftChild(self, pos):
return 2 * pos
# Function to return the position of
# the right child for the node currently
# at pos
def rightChild(self, pos):
return (2 * pos) + 1
# Function that returns true if the passed
# node is a leaf node
def isLeaf(self, pos):
if pos >= (self.size//2) and pos <= self.size:
return True
return False
# Function to swap two nodes of the heap
def swap(self, fpos, spos):
self.Heap[fpos], self.Heap[spos] = (self.Heap[spos],
self.Heap[fpos])
# Function to heapify the node at pos
def maxHeapify(self, pos):
# If the node is a non-leaf node and smaller
# than any of its child
if not self.isLeaf(pos):
if (self.Heap[pos] < self.Heap[self.leftChild(pos)] or
self.Heap[pos] < self.Heap[self.rightChild(pos)]):
# Swap with the left child and heapify
# the left child
if (self.Heap[self.leftChild(pos)] >
self.Heap[self.rightChild(pos)]):
self.swap(pos, self.leftChild(pos))
self.maxHeapify(self.leftChild(pos))
# Swap with the right child and heapify
# the right child
else:
self.swap(pos, self.rightChild(pos))
self.maxHeapify(self.rightChild(pos))
# Function to insert a node into the heap
def insert(self, element):
if self.size >= self.maxsize:
return
self.size += 1
self.Heap[self.size] = element
current = self.size
while (self.Heap[current] >
self.Heap[self.parent(current)]):
self.swap(current, self.parent(current))
current = self.parent(current)
# Function to print the contents of the heap
def Print(self):
for i in range(1, (self.size // 2) + 1):
print(" PARENT : " + str(self.Heap[i]) +
" LEFT CHILD : " + str(self.Heap[2 * i]) +
" RIGHT CHILD : " + str(self.Heap[2 * i + 1]))
# Function to remove and return the maximum
# element from the heap
def extractMax(self):
popped = self.Heap[self.FRONT]
self.Heap[self.FRONT] = self.Heap[self.size]
self.size -= 1
self.maxHeapify(self.FRONT)
return poppedinsert를 잘 봐야 할 것 같다.
element를 하나 추가하면 특정 공간에 element를 넣는다.
그리고 while 문에서 비교하고 swap 하는 부분을 하게 된다. (현재 위치에 있는 값보다 parent에 있는 값이 더 작아지면 멈추게 된다.)
def insert(self, element):
if self.size >= self.maxsize:
return
self.size += 1
self.Heap[self.size] = element
current = self.size
while (self.Heap[current] >
self.Heap[self.parent(current)]):
self.swap(current, self.parent(current))
current = self.parent(current)## 공간을 15개 정도 정해둔다.
maxHeap = MaxHeap(15)
## 5를 넣는다.
maxHeap.insert(5)
sys.maxsize,5,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0
maxHeap.insert(3)parent node인 0에서 나온 5와 현재 노드에서 나온 3을 비교한다.
3>5이므로 넘어간다.
sys.maxsize,5,3,0,0,0,0,0,0,0,0,0,0,0,0,0
maxHeap.insert(17)swap을 통해 현재 노드와 부모 노드의 값을 변경해준다.
sys.maxsize,5,3,17,0,0,0,0,0,0,0,0,0,0,0,0
-> sys.maxsize,5,17,3,0,0,0,0,0,0,0,0,0,0,0,0
parent node인 1을 current node랑 바꿔준다.
그럼 변경된 parent node인 0에서 나온 5와 현재 노드에서 나온 17을 비교한다.
17>5 -> True 이므로 while 문에 들어간다.
swap을 통해 현재 노드와 부모 노드의 값을 변경해준다.
sys.maxsize,5,17,3,0,0,0,0,0,0,0,0,0,0,0,0
-> sys.maxsize,17,5,3,0,0,0,0,0,0,0,0,0,0,0,0
parent node인 0을 current node랑 바꿔준다.
그럼 변경된 parent node인 0에서 나온 17과 현재 노드에서 나온 17을 비교한다.
17 < 17 -> False
sys.maxsize,17,5,3,0,0,0,0,0,0,0,0,0,0,0,0
maxHeap.insert(10)sys.maxsize,17,5,3,10,0,0,0,0,0,0,0,0,0,0,0
sys.maxsize,17,5,3,10,0,0,0,0,0,0,0,0,0,0,0
-> sys.maxsize,17,10,3,5,0,0,0,0,0,0,0,0,0,0,0
parent node인 2를 current node랑 바꿔준다.
parent node인 1에서 나온 17과 현재 노드에서 나온 10을 비교한다.
10>17 -> False 이므로 중지
print('The maxHeap is ')
maxHeap = MaxHeap(15)
maxHeap.insert(5)
maxHeap.insert(3)
maxHeap.insert(17)
maxHeap.insert(10)
maxHeap.insert(84)
maxHeap.insert(19)
maxHeap.insert(6)
maxHeap.insert(22)
maxHeap.insert(9)
maxHeap.Print()
print("The Max val is " + str(maxHeap.extractMax()))Heap : [9223372036854775807, 22, 17, 19, 9, 10, 5, 6, 3, 9, 0, 0, 0, 0, 0, 0]
extracMax는 제일 가장 큰 값을 뽑고 나서 다시 max-heap을 유지하게 하는 코드이다.
Python Code for Max Heap Data Structure
def max_heapify(A,k):
l = left(k)
r = right(k)
if l < len(A) and A[l] > A[k]:
largest = l
else:
largest = k
if r < len(A) and A[r] > A[largest]:
largest = r
if largest != k:
A[k], A[largest] = A[largest], A[k]
max_heapify(A, largest)
def left(k):
return 2 * k + 1
def right(k):
return 2 * k + 2
def build_max_heap(A):
n = int((len(A)//2)-1)
for k in range(n, -1, -1):
max_heapify(A,k)
A = [3,9,2,1,4,5]
build_max_heap(A)Python Code for Min Heap Data Structure
def min_heapify(A,k):
l = left(k)
r = right(k)
if l < len(A) and A[l] < A[k]:
smallest = l
else:
smallest = k
if r < len(A) and A[r] < A[smallest]:
smallest = r
if smallest != k:
A[k], A[smallest] = A[smallest], A[k]
min_heapify(A, smallest)
def left(k):
return 2 * k + 1
def right(k):
return 2 * k + 2
def build_min_heap(A):
n = int((len(A)//2)-1)
for k in range(n, -1, -1):
min_heapify(A,k)
A = [3,9,2,1,4,5]
build_min_heap(A)
print(A)Using Library functions
기본적으로 minheap이기 때문에 max로 하고 싶다면 주어진 값에 -를 붙여야 한다!
from heapq import heappop, heappush, heapify
heap = []
heapify(heap)
heappush(heap, -1 * 10)
heappush(heap, -1 * 400)
heappush(heap, -1 * 20)
heappush(heap, -1 * 30)
# printing the value of maximum element
print("Head value of heap : "+str(-1 * heap[0]))
# printing the elements of the heap
print("The heap elements : ")
for i in heap:
print(-1 * i, end = ' ')
print("\n")Head value of heap : 400
The heap elements :
400 30 20 10
element = heappop(heap)
# printing the elements of the heap
print("The heap elements : ")
for i in heap:
print(-1 * i, end = ' ')The heap elements :
30 10 20
-400
결론
일단은 사실 내가 이것을 사용할 일이 있을지는 모르겠지만, 컴퓨터 알고리즘적으로 이해하는데 많은 도움이 되었고,
고급 프로그래밍으로 갈수록 이러한 힙에 대한 개념을 많이 사용하니 잘 알아두고 있어야겠다.
https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html
[자료구조] 힙(heap)이란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
https://tacademy.skplanet.com/live/player/onlineLectureDetail.action?seq=83&preType=my
컴퓨터 알고리즘 초급 | T아카데미 온라인강의
컴퓨터 알고리즘은 성공적인 프로그래밍을 위한 필수적인 과목입니다. 본 과정에서는 컴퓨터 알고리즘의 정의에 대해 학습하고 필요성을 인식하며 이에 대한 기본내용을 학습합니다. 또..
tacademy.skplanet.com
'분석 Python > 책 구현 리뷰' 카테고리의 다른 글
| [책] Deep Reinforcement Learning in Action Code Link (0) | 2021.02.22 |
|---|---|
| 책 러닝 텐서플로 - 코드 (0) | 2020.01.11 |
| 미술관에 GAN 딥러닝(Generative Deep Learning) Code (0) | 2019.11.17 |
| 파이썬을 활용한 딥러닝 전이학습 책 Code (0) | 2019.11.17 |
| [ Python ] 자신만의 예외 클래스 정의하기 - 슬기로운 파이썬 트릭 책 中 (0) | 2019.09.29 |