728x90
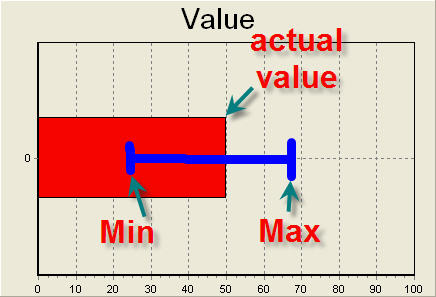
제한 조건을 이용해서, 솔루션이 아닌 제한 조건을 만족하는 범위를 찾고자 하는 문제를 풀고 싶었다.
해당 문제에서는 순차적 경우를 가정해서 문제를 풀기로 하였다.
아직 상상으로 해보는 것은 특정 인자가 결정이 되면, 다른 인자도 영향을 받기 때문에, 순차적으로 밖에 생각이 들지 않는다.
그래서 인자를 하나씩 찾아나가는 것을 진행해 봤다.
기본 제한 조건은 다음과 같이 진행했다.
$ 0 \le x \le 100$
$ 0 \le y \le 100$
$ 0 \le z \le 100$
$ 0 \le 2*x+7*y+3*z \le 50$
$ 0 \le 3*x-5*y+7*z \le 45$
$ 0 \le 5*x+2*y-6*z \le 37$
인자들의 연관성의 가정은 x->y->z로 가정을 하고, 한 개의 인자가 결정되거나 범위가 축소됨에 따라 다른 인자들의 범위도 바뀌는 것을 구현해봤다.
from ortools.sat.python import cp_model
import numpy as np
class VarArraySolutionCollector(cp_model.CpSolverSolutionCallback):
"""Print intermediate solutions."""
def __init__(self, variables):
cp_model.CpSolverSolutionCallback.__init__(self)
self.__variables = variables
self.__solution_count = 0
self.__get_result = []
def on_solution_callback(self):
self.__solution_count += 1
for v in self.__variables:
# print('%s=%i' % (v, self.Value(v)), end=' ')
self.__get_result.append(self.Value(v))
def solution_count(self):
return self.__solution_count
def solution_list(self) :
return np.unique(self.__get_result).tolist()
class GetRange_all_solution(object) :
def __init__(self,) :
pass
def define_model(self,) :
model = cp_model.CpModel()
var_upper_bound = max(20, 100, 37)
var = dict()
var["x"] = model.NewIntVar(0, var_upper_bound, 'x')
var["y"] = model.NewIntVar(0, var_upper_bound, 'y')
var["z"] = model.NewIntVar(0, var_upper_bound, 'z')
model.Add(2*var["x"] + 7*var["y"] + 3*var["z"] <= 50)
model.Add(3*var["x"] - 5*var["y"] + 7*var["z"] <= 45)
model.Add(5*var["x"] + 2*var["y"] - 6*var["z"] <= 37)
self.model = model
self.var = var
def __call__(self, solution , **kwargs) :
self.define_model()
for key , value in kwargs.items() :
if key == "x_bound" :
self.model.AddLinearConstraint(self.var["x"],value[0] , value[1])
elif key == "y_bound" :
self.model.AddLinearConstraint(self.var["y"],value[0] , value[1])
elif key == "z_bound" :
self.model.AddLinearConstraint(self.var["z"],value[0] , value[1])
# list(self.var.items())
self.solver = cp_model.CpSolver()
solution_collector = VarArraySolutionCollector([self.var[solution]])
status = self.solver.SearchForAllSolutions(self.model, solution_collector)
return solution_collector.solution_list()
결과는 다음과 같다.
get_range_model = GetRange_all_solution()
result = get_range_model("x")
result
# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
get_range_model = GetRange_all_solution()
result = get_range_model("y",x_bound=[0,5])
result
# [0, 1, 2, 3, 4, 5, 6, 7]
get_range_model = GetRange_all_solution()
result = get_range_model("z",x_bound=[0,5],y_bound=[0,7])
result
# [0, 1, 2, 3, 4, 5, 6, 7, 8]
현재는 IntVar만 진행을 해봤고, 점점 확장을 시도해보려고 하지만, 이러한 것들이 일반화가 되게 구현을 하려면 어떻게 해야 할지는 좀 고민이 된다.
그리고 적용하는 순서가 순차적이지 않은 경우에 적용이 가능할지는 의문이긴 하다.
혹시 이러한 처리를 해주는 패키지를 안다면 댓글에 남겨주시길 부탁드립니다 :)
1. 제한 조건을 만족하는 (min, max) 범위 찾아 주는 것
2. 제한 조건을 만족하는 후보군들 찾아주기
3. 등등...
4. 이러한 것들을 일반화해주는 패키지
'분석 Python > 구현 및 자료' 카테고리의 다른 글
| notion-py를 사용하여 캘린더 만들기 (0) | 2021.08.08 |
|---|---|
| Python) Yield 에 대해서 알아보기 (0) | 2021.08.07 |
| pycaret 2.3.1) tune_model hyperopt example (0) | 2021.06.20 |
| numpy에서 dict을 이용해서 값을 바꾸는 방법 (2) | 2021.06.06 |
| tqdm) print대신에 tqdm을 이용해서 logging 방법 (0) | 2021.05.15 |