GPT를 활용하여 작성하였습니다
배경
어쩌다가 뉴스 기사를 통해 보게 되었고, 내용을 대충 보니 데이터를 어떻게 쌓으면 되는지 그리고 어떤 식으로 학습하면 되는지 그리고 깃헙을 제공하다 보니, 관심을 가지게 되었고, 읽게 되었습니다.
그래서 이 논문을 통해 알고자 하는 부분은 어떻게 데이터를 뽑았는 지, 그리고 어떻게 저렴한 비용으로 해당 모델을 만들 수 있는 지를 알고자 읽어보게 되었습니다.
이 논문의 핵심 내용은 Test-time scaling(테스트 시 스케일링)이라는 개념을 활용하여 언어 모델의 성능을 향상시키는 방법을 연구하는 것입니다. 기존에 OpenAI의 o1 모델이 이를 구현했지만, 구체적인 방법이 공개되지 않아 이를 복제하려는 여러 시도가 있었습니다. 연구진은 가능한 한 가장 단순한 방식으로 테스트 시 스케일링을 구현하고, 강력한 추론 성능을 달성하는 것을 목표로 합니다.
개요
연구의 주요 내용
- s1K 데이터셋 구축
- 1,000개의 질문과 추론 과정(reasoning traces)을 포함한 데이터셋을 생성.
- Google Gemini Thinking Experimental에서 답변을 가져와 정제.
- 데이터 선정 기준: 난이도(Difficulty), 다양성(Diversity), 품질(Quality)
- 실험 결과, 무작위 선택 또는 단순한 다양성 최대화 방식보다 이 기준을 조합한 방법이 훨씬 성능이 우수함을 확인.
- Budget Forcing 기법 개발 (Test-time Scaling 제어 방법)
- 모델이 생성하는 사고 과정(Thinking process) 길이를 조절하는 기법을 개발.
- 두 가지 방식으로 모델의 사고 시간을 제어함:
① 일정 개수 이상의 추론 토큰이 생성되면 강제로 사고 과정 종료 → 모델이 답변을 생성하도록 유도.
② 모델이 너무 빨리 종료하려 하면 "Wait" 토큰을 추가 → 모델이 더 깊게 사고하도록 유도. - 이 방식은 모델이 자기 답변을 재검토하여 오류를 수정할 수 있도록 돕는 역할을 함
- 모델 학습 및 성능 평가
- Qwen2.5-32B-Instruct 모델을 s1K 데이터셋으로 지도 학습(Supervised Fine-Tuning, SFT) 진행.
- 학습 시간: H100 GPU 16개에서 단 26분
- 학습 후 Budget Forcing 기법을 적용하여 Test-time 연산을 조절
- OpenAI의 o1-preview 모델보다 경쟁력 있는 성능을 달성
→ 특히 MATH 및 AIME24 문제에서 o1-preview 대비 최대 27% 성능 향상 - Test-time scaling이 실제로 작동함을 입증 (Budget Forcing을 활용할수록 성능이 선형적으로 증가하는 패턴 관찰)
연구의 핵심 기여
- 단순한 방법(test-time scaling + budget forcing)으로 언어 모델의 추론 능력을 크게 향상.
- Budget Forcing이 가장 효과적인 방법임을 확인.
- 모델의 사고 시간을 직접 제어할 수 있는 완벽한 컨트롤 가능성을 제공하며, 성능 향상이 선형적으로 이루어짐.
- 적은 데이터로도 효과적인 학습이 가능하다는 것을 입증.
- 소규모 데이터셋(1,000개 샘플)과 간단한 기법(Budget Forcing)만으로 강력한 추론 성능을 달성
- 1,000개 샘플을 선정하는 기준(난이도, 다양성, 품질)이 매우 중요함을 입증.
- 59K 샘플(전체 데이터 풀)로 학습해도 성능 향상 효과가 크지 않았음 → 데이터 선정의 중요성 재확인
- 연구의 코드, 데이터셋, 모델을 오픈소스(https://github.com/simplescaling/s1)로 공개, 후속 연구의 기초를 제공.

기존 방식
기존의 언어 모델(LM) 성능 향상은 주로 훈련 시(Train-time) 연산을 확장하는 방식으로 이루어져 왔습니다. 즉, **대규모 자기지도학습(Self-Supervised Learning)**을 활용하여 모델을 점점 더 크게 확장하는 방식이었습니다. (Kaplan et al., 2020; Hoffmann et al., 2022)
그러나 최근 OpenAI의 o1 모델은 **테스트 시(Test-time) 연산을 증가시키는 새로운 확장 패러다임(Test-time scaling)**을 통해 뛰어난 추론 성능을 달성하며, 이 접근법이 효과적임을 입증했습니다. 하지만 OpenAI는 그 방법을 공개하지 않았고, 여러 연구팀이 이를 복제하려 시도했습니다.
기존 복제 시도들은 보통 다음과 같은 방법을 사용했습니다:
✅ 강화학습(RL) 기반 접근 → 수백만 개의 샘플과 다단계 훈련 필요 (DeepSeek R1 등)
✅ 몬테카를로 트리 탐색(Monte Carlo Tree Search, MCTS) 활용
✅ 다중 에이전트(Multi-Agent) 학습 방법
하지만 이러한 방법들은 복잡하고 연산량이 많으며, 아직 명확한 Test-time scaling을 복제한 사례는 부족했습니다.
연구진은 이에 대해 **"가장 단순한 방식으로 Test-time scaling과 강력한 추론 성능을 모두 달성하는 방법이 무엇인가?"**라는 질문을 던졌습니다.
데이터 선정 과정
여기서 결국 강조하는 것은 역시 데이터 품질입니다.
그래서 2. Reasoning Data Curation (데이터 선정 과정) 에 어떻게 선정하는지에 대해서 상세하게 적어놓은 것을 확인했습니다.
연구진은 s1K(1,000개 샘플) 데이터셋을 만들기 위해 59,029개의 질문을 수집한 후 필터링 과정을 거쳤습니다.
크게 16개의 다양한 출처에서 데이터를 수집했다고 합니다.
1. 초기 데이터셋 구축 (59K 샘플 수집)
데이터 선정 원칙(3가지):
✅ 품질(Quality): 데이터셋이 높은 품질을 유지해야 하며, 형식 오류나 낮은 품질의 데이터를 제거.
✅ 난이도(Difficulty): 어려운 문제여야 하며, 높은 수준의 추론 능력을 요구해야 함.
✅ 다양성(Diversity): 다양한 분야의 데이터를 포함하여, 여러 유형의 추론 문제를 다룰 수 있도록 구성.
📌 수집된 주요 데이터셋(기존):
- NuminaMATH (30,660개 수학 문제) - 온라인에서 수집된 수학 문제
- AIME 문제 (1983~2021) - 미국 수학 경시대회 문제
- OlympicArena (4,250개 문제) - 천문학, 생물학, 화학, 컴퓨터 과학, 지리학, 수학, 물리학 포함
- OmniMath (4,238개 문제) - 경시대회 수준의 수학 문제
- AGIEval (2,385개 문제) - SAT, LSAT 등의 표준 시험에서 추출된 문제 (영어, 법학, 논리 문제 포함)
📌 수집된 주요 데이터셋(신규):
- s1-prob (182개 문제) - Stanford PhD 확률 시험에서 수집된 난이도 높은 확률 문제
- s1-teasers (23개 문제) - 금융 및 퀀트 면접 문제로 사용되는 고난도 퍼즐 문제
➡ 총 59K 샘플을 수집한 후, Google Gemini Flash Thinking API를 이용해 추론 과정(reasoning trace)과 해답을 생성
💡 데이터 정제 과정
- 평가 데이터셋(MATH500, GPQA Diamond, AIME24)과 중복 여부 검사 (8-gram 비교)
- 중복 데이터 제거 및 형식 오류 수정
2. 최종 1K 샘플 선정 과정
59K 샘플을 모두 학습에 사용할 수도 있지만, 연구진은 최소한의 데이터로 최적의 성능을 내는 방법을 찾고자 했습니다. 이를 위해 3단계 필터링을 진행했습니다.
1️⃣ 품질(Quality) 필터링
- API 오류가 발생한 데이터 제거 → 59K → 54,116개
- 형식 오류(ASCII 아트, 잘못된 이미지 참조 등) 포함 데이터 제거 → 51,581개
- 연구진이 고품질 데이터셋으로 판단한 384개 샘플은 추가 필터링 없이 유지
2️⃣ 난이도(Difficulty) 필터링
- Qwen2.5-7B 및 Qwen2.5-32B 모델을 사용하여 모든 문제를 평가
- Claude 3.5 Sonnet이 모델의 답변과 정답을 비교하여 난이도 평가
- 너무 쉬운 문제(두 모델이 모두 정답을 맞힌 문제) 제거 → 24,496개로 축소
- 난이도가 높을수록 reasoning trace 길이가 길다는 가정하에, reasoning trace 길이를 기준으로 추가 필터링
3️⃣ 다양성(Diversity) 필터링
- Claude 3.5 Sonnet을 사용해 모든 질문을 수학 주제 분류 체계(MSC)에 따라 분류
- 도메인을 균등하게 샘플링 → 다양한 분야(수학, 물리, 생물, 경제학 등)에서 문제를 선정
- 최종적으로 1,000개의 균형 잡힌 샘플(s1K) 생성
최종적으로 50개 도메인에서 1,000개의 문제를 선정하여 s1K 데이터셋을 구축
3. Test-time scaling
Test-time scaling은 테스트 시 추가 연산을 활용하여 모델 성능을 향상시키는 접근법입니다. 이 연구에서는 Budget Forcing이라는 기법을 사용하여, 모델이 사고하는 시간(Thinking duration)을 제어하는 방법을 제안합니다.
아래 그림은 openai 에서 소개한 하나의 예시이고 이걸 이제 Budget Forcing을 썻을 때 답변 개선에 대한 예제입니다.
이 문장은 Budget Forcing 기법이 어떻게 모델의 답변을 개선하는지 설명하는 예제입니다.
📌 설명:
- 모델이 원래 "...is 2."에서 멈추려 했음.
- 하지만 연구진이 "Wait" 토큰을 추가하여 모델이 계속해서 사고하도록 유도함.
- 그 결과, 모델이 자신의 답변을 재검토하고 수정하는 효과가 발생함.
➡ 즉, Budget Forcing을 사용하면 모델이 너무 빨리 답변을 끝내지 않고, 좀 더 깊이 고민할 수 있도록 유도할 수 있음! 🚀

1. Test-time Scaling 방법론
연구진은 Test-time Scaling 기법을 두 가지 유형으로 분류했습니다.
✅ 1) Sequential Scaling (순차적 확장)
- 이전 연산 결과가 이후 연산에 영향을 주는 방식
- 예: 긴 reasoning trace를 통해 점진적으로 더 깊은 사고 수행
- Budget Forcing 기법이 여기에 해당
✅ 2) Parallel Scaling (병렬적 확장)
- 독립적인 여러 연산을 동시에 수행한 후 다수결(Majority Voting)로 결정
- 예: 다수의 답변을 생성한 후 가장 많이 등장한 답을 선택
➡ 연구진은 순차적 확장이 더 효과적이라고 보고, Budget Forcing을 기반으로 연구를 진행했습니다.
📌 Budget Forcing 기법 (순차적 확장을 위한 방법)
Budget Forcing은 디코딩 과정에서 모델이 사고하는 시간(Thinking duration)을 직접 제어하는 기법입니다.
1️⃣ 최대 사고(Thinking) 토큰 수 제한
- 모델이 너무 긴 추론을 수행하지 않도록 강제 종료
- 방법: "Final Answer:" 토큰 추가하여 모델이 답변을 생성하도록 유도
2️⃣ 최소 사고(Thinking) 토큰 수 제한
- 모델이 너무 빨리 멈추려 하면 "Wait" 토큰을 추가
- 이를 통해 모델이 자기 답변을 검토하고 오류를 수정할 기회를 부여
📌 예제 (Figure 3):
- 모델이 "…is 2."에서 멈추려 했지만, 연구진이 "Wait"을 추가하여 더 깊은 사고를 하도록 유도
- 결과적으로 모델이 자신의 답변을 수정하는 효과를 보임
➡ 간단한 방법이지만, 효과적으로 모델의 reasoning 능력을 향상시킬 수 있음
Baselines (비교 실험 방법)
Budget Forcing 기법의 성능을 평가하기 위해 다른 기법들과 비교 실험을 진행했습니다.
✅ 1) Conditional Length-control Methods (길이 조건부 제어 기법)
- 모델에게 추론을 수행할 길이를 사전에 알려주는 방식
- (a) Token-conditional control: 사고 토큰 개수를 직접 지정
- (b) Step-conditional control: 사고 과정을 단계별로 제어 (각 단계 ≈ 100 토큰)
- (c) Class-conditional control: 모델에게 "짧게 생각해라" 또는 "길게 생각해라"와 같은 프롬프트 제공
✅ 2) Rejection Sampling (거절 샘플링 기법)
- 모델이 생성한 응답이 정해진 연산량 내에서 맞을 때까지 계속 샘플링
- 이론적으로 최적의 결과를 제공할 수 있지만, 연산량이 많이 필요함
➡ Budget Forcing 기법은 위 방법들보다 더 간단하면서도 효과적인 방식임을 입증
2. Test-time Scaling 성능 평가 지표
연구진은 Test-time Scaling 기법을 평가하기 위한 3가지 주요 지표를 정의했습니다.
1️⃣ Control (조절 가능성, %)
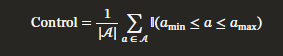
- 모델이 사용자가 원하는 만큼 사고 시간을 조절할 수 있는지 측정
- 100%에 가까울수록 사용자가 모델의 Test-time 연산을 완벽하게 제어할 수 있음
2️⃣ Scaling (성능 증가율, 기울기)
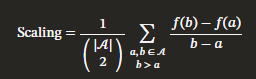
- Test-time compute(연산량)에 따라 성능이 얼마나 증가하는지 측정
- 기울기가 클수록 적은 연산량 증가로도 성능 향상이 큼
3️⃣ Performance (최대 성능, %)
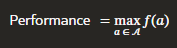
- 벤치마크에서 달성 가능한 최고 성능을 측정
- Test-time scaling이 제대로 동작한다면, 더 많은 연산을 할수록 성능이 증가해야 함
➡ Budget Forcing 기법이 높은 조절 가능성과 뛰어난 성능 증가율을 보였음
3. Sequential vs Parallel Scaling 비교 (Figure 4)

(a) Sequential Scaling (Budget Forcing 적용)
- Test-time compute를 늘릴수록 성능이 선형적으로 증가하는 패턴 보임
- 모델이 사고를 중단하려 할 때 2/4/6번씩 "Wait"을 추가하여 더 깊은 reasoning을 유도
(b) Parallel Scaling (Majority Voting 적용)
- 여러 번의 독립적인 추론을 수행하고 다수결로 답을 결정
- 병렬 방식이지만 추가 연산량에 비해 성능 향상은 제한적
➡ 결과적으로 Budget Forcing이 Test-time Scaling 기법 중 가장 효과적임을 입증 🚀
4. 실험 결과 (Results)
이 연구에서는 s1-32B 모델이 Test-time scaling을 효과적으로 수행하며, 적은 데이터로도 강력한 추론 성능을 발휘할 수 있음을 검증했습니다.
1. 실험 환경
모델 학습 (Training)
- Qwen2.5-32B-Instruct 모델을 s1K(1,000개 샘플) 데이터로 지도 학습(Supervised Fine-Tuning, SFT)
- 학습 시간: 26분 (NVIDIA H100 GPU 16개 사용)
- PyTorch FSDP (Fully Sharded Data Parallel) 프레임워크 활용
모델 평가 (Evaluation)
- 세 가지 대표적인 추론 벤치마크에서 성능 평가
1️⃣ AIME24 (2024년 미국 수학 경시대회 문제, 30문항)
2️⃣ MATH500 (수학 경시대회 문제 500문항)
3️⃣ GPQA Diamond (박사급 과학 문제 198문항)
➡ 기존 연구(OpenAI, DeepSeek-AI 등)에서 사용한 벤치마크와 동일한 기준 적용
비교 대상 모델 (Baseline Models)
- OpenAI o1 시리즈 (테스트 시 스케일링 개념을 처음 제안한 비공개 모델)
- DeepSeek r1 시리즈 (800K 샘플을 사용해 OpenAI o1 수준을 복제한 모델)
- Qwen QwQ-32B-preview (비공개 방법론 기반의 32B 오픈 모델)
- Google Gemini 2.0 Flash Thinking Experimental (s1-32B가 distillation한 모델)
- Sky-T1-32B-Preview 및 Bespoke-32B (오픈 모델, r1 및 QwQ-32B-preview 기반 데이터 활용)
➡ s1-32B는 모델 가중치(weights), 데이터셋, 코드까지 모두 오픈 소스로 제공되는 유일한 모델
2 성능 분석 (Performance Analysis)
1️⃣ Test-time Scaling 성능 검증
📌 분석
- s1-32B 모델에 Budget Forcing을 적용했을 때, Test-time compute를 증가시킬수록 성능이 점진적으로 향상됨
- AIME24 문제에서 6배 이상의 Test-time compute를 적용하면 성능 향상이 더 이상 증가하지 않음 (포화점 존재)
- End-of-thinking token을 너무 자주 억제하면, 모델이 반복 루프에 빠질 위험이 있음
- Baseline 모델(Qwen2.5-32B-Instruct)의 Majority Voting 기법은 s1-32B보다 성능이 낮음
- 이는 Sequential Scaling이 Parallel Scaling(병렬 다수결)보다 효과적임을 입증
➡ Budget Forcing을 적용한 s1-32B는 기존의 단순 Majority Voting 기법보다 훨씬 우수한 성능을 보임
2️⃣ Sample Efficiency (데이터 효율성 비교)

📌 Table 1 분석
- s1-32B는 가장 샘플 효율적인 오픈 데이터 reasoning 모델
- Qwen2.5-32B-Instruct 대비, 단 1,000개 샘플 추가 학습만으로 성능이 크게 향상됨
- DeepSeek r1-32B는 더 높은 성능을 보이지만, 800K 샘플을 사용
- s1-32B는 1,000개 샘플만 사용하고도, 800K 샘플을 학습한 r1 모델에 근접한 성능을 보임
📌 AIME24 벤치마크 성능 비교
- s1-32B (56.7%) ≈ Gemini 2.0 (60.0%)
- s1-32B는 Gemini 2.0을 distillation한 모델임에도 성능 차이가 크지 않음 → 효과적인 distillation 절차를 거쳤음을 의미
세부 실험 분석
1. 데이터의 양, 다양성, 난이도가 성능에 미치는 영향
연구진은 **s1K 데이터셋(1,000개 샘플)**을 구축할 때, 품질(Quality), 난이도(Difficulty), 다양성(Diversity) 세 가지 기준을 적용했습니다.
이번 실험에서는 각각의 기준을 개별적으로 적용했을 때 s1K 대비 성능이 어떻게 변하는지 확인했습니다.
📌 실험 결과 (Table 2 분석)

- 1K-random (무작위 1,000개 샘플 선정)
- 난이도와 다양성을 고려하지 않고 무작위로 선택
- s1K 대비 모든 벤치마크에서 성능이 크게 감소
- AIME24: -26.7%, MATH500: -4.8%, GPQA: -12.6%
- 1K-diverse (다양성 극대화, 난이도 고려 X)
- 모든 도메인에서 균등하게 샘플을 선택했지만 난이도는 고려하지 않음
- AIME24에서 가장 낮은 성능 (-40%)
- 다양성만 고려하는 것은 오히려 성능을 떨어뜨림
- 1K-longest (가장 긴 reasoning trace 샘플 선택, 난이도 극대화)
- 긴 reasoning trace를 가진 문제만 선택
- GPQA 성능은 향상(+2%)되었지만, AIME24와 MATH500에서는 성능 저하
- 난이도만 고려해도 최적의 성능이 나오지는 않음
- 59K-full (전체 59K 샘플 사용)
- s1K보다 높은 성능을 보이지만, 연산 비용이 너무 큼
- GPU 시간: 394 H100 GPU 시간 필요 (s1K는 7시간)
➡ 결론:
✅ 품질(Quality), 난이도(Difficulty), 다양성(Diversity)을 조합한 s1K가 가장 효율적인 성능을 보임
✅ 단순히 데이터를 늘리는 것보다, 적은 샘플이라도 잘 구성된 데이터셋이 성능 향상에 더 중요함
연구진은 Budget Forcing 기법과 기존의 Test-time Scaling 기법들을 비교하여 어떤 방법이 가장 효과적인지 분석했습니다.
2. Test-time Scaling 기법 비교 실험
연구진은 Budget Forcing 기법과 기존의 Test-time Scaling 기법들을 비교하여 어떤 방법이 가장 효과적인지 분석했습니다.

➡ 결론:
✅ Budget Forcing(BF)이 가장 높은 성능과 조절 가능성을 제공함
✅ TCC, SCC, CCC 같은 기존 방법은 Test-time Scaling 성능이 낮음
✅ Rejection Sampling(RS)은 오히려 성능이 감소 (Scaling: -35%)
3 Budget Forcing 기법 세부 실험 (Extrapolation 방법 비교)
Budget Forcing에서 "Wait" 같은 특정 문자열을 추가했을 때, 모델 성능이 어떻게 달라지는지 실험했습니다.

➡ 결론:
✅ Budget Forcing에서 "Wait"을 추가하는 것이 가장 높은 성능을 보임
✅ "Hmm"와 "Alternatively"도 성능 향상 효과는 있지만, "Wait"이 가장 효과적
✅ 무작정 사고 시간을 늘리는 것이 아니라, 특정한 방식으로 유도하는 것이 중요
4. Rejection Sampling 기법의 한계
📌 Figure 6 분석
- Rejection Sampling은 샘플을 특정 길이 이하로 맞출 때까지 계속 생성하는 방법
- 실험 결과, Test-time compute가 증가할수록 성능이 오히려 하락하는 경향을 보임
- 짧은 추론 과정에서 정답에 도달하는 경우가 많고, 긴 추론 과정에서는 오히려 실수가 많아짐
➡ 결론:
✅ Rejection Sampling은 Test-time Scaling 기법으로 적절하지 않음
✅ 긴 reasoning trace가 항상 좋은 것은 아니며, 효과적인 사고 과정이 중요함
연구 결론 및 기여
✅ 품질(Quality), 난이도(Difficulty), 다양성(Diversity) 세 가지를 조합해야 최적의 데이터셋이 됨
✅ Budget Forcing이 가장 효과적인 Test-time Scaling 기법으로 검증됨
✅ "Wait" 같은 특정 토큰을 추가하면 모델 성능을 더욱 향상시킬 수 있음
✅ Rejection Sampling은 오히려 성능이 감소하는 경향을 보이며, 적절한 방법이 아님
➡ 결론: Budget Forcing이 가장 효과적인 Test-time Scaling 기법이며, 적은 데이터로도 강력한 성능을 낼 수 있는 방법임을 입증 🚀
데이터
s1-prob : 확률론 문제 (Probability Problem)
📌 질문:
독립적인 평균 0인 확률변수 {Xn}\{X_n\}이 주어져 있으며, Sn=X1+X2+⋯+XnS_n = X_1 + X_2 + \cdots + X_n로 정의된다.
또한, supnE(∣Sn∣)<∞\sup_n E(|S_n|) < \infty라고 가정할 때, 임의의 a.s. 유한 정지시간 TT에 대해 E(ST)=0E(S_T) = 0임을 보여라.
📌 해설:
- 이는 **멈춤 시간(Stopping Time)**과 **마팅게일(Martingale)**에 관한 문제입니다.
- Ottaviani's Inequality를 활용하여 E(supn∣Sn∣)<∞E(\sup_n |S_n|) < \infty를 증명.
- 이후 **선택 정리(Optional Stopping Theorem, OST)**을 적용하여 E(ST∧n)=0E(S_{T \wedge n}) = 0임을 보이고,
- **Vitali의 수렴 정리(Vitali's Theorem)**를 사용하여 E(ST)=0E(S_T) = 0을 결론적으로 도출.
✅ 핵심 개념: 마팅게일 성질과 정지시간 이론을 활용하여, 기대값 보존을 증명하는 문제.
| question |
solution
|
|
Let X_1, X_2, \cdots be independent, with E(X_n) = 0 for all n. Let S_n = X_1 + X_2 + \cdots + X_n and suppose \sup_n E(|S_n|) < \infty. Let T be an a.s. finite stopping time with respect to the natural filtration of the X's. Show E(S_T) = 0. |
We have independent mean-zero random variables $X_1, X_2, \ldots$ such that $\sup_{n \geq 1} \mathbb{E}|X_n| =C < \infty$, where $S_1 = \sum_{k=1}^n X_k$. We shall use \textit{Ottaviani's Inequality}. For completeness we are adding a proof of it here. Take any $t,s >0$. Let $B_n:=(|S_1|, |S_2|, \ldots, |S_{n-1}| < t+s, |S_n| \geq t+s)$ for all $n \geq 1$. Clearly the events $B_n$'s are mutually disjoint. Using the fact that $B_k$ is independent to $S_n-S_k$ for all $n \geq k$, we have the following. \begin{align*} \mathbb{P}\left(\max_{k=1}^n |S_k| \geq t+s\right) = \mathbb{P}\left(\bigcup_{k=1}^n B_k\right) = \sum_{k=1}^n \mathbb{P}(B_k) &= \sum_{k=1}^n \mathbb{P}(B_k, |S_n| \geq t) + \sum_{k=1}^n \mathbb{P}(B_k, |S_n| < t) \\ & \leq \mathbb{P}(|S_n| \geq t) + \sum_{k=1}^{n-1} \mathbb{P}(B_k, |S_n| < t) \\ &\leq \mathbb{P}(|S_n| \geq t) + \sum_{k=1}^{n-1} \mathbb{P}(B_k, |S_n-S_k| > s) \\ &\leq \mathbb{P}(|S_n| \geq t) + \sum_{k=1}^{n-1} \mathbb{P}(B_k) \mathbb{P}(|S_n-S_k| > s) \\ & \leq \mathbb{P}(|S_n| \geq t) + \dfrac{2C}{s}\sum_{k=1}^{n-1} \mathbb{P}(B_k) \leq \mathbb{P}(|S_n| \geq t)+ \dfrac{2C\mathbb{P}(\max_{k=1}^n |S_k| \geq t+s)}{s}. \end{align*} Choose $s >2C$. Then \begin{align*} \left(1-\dfrac{2C}{s} \right) \mathbb{P} \left(\max_{k=1}^n |S_k| \geq t+s \right) = \left(1-\dfrac{2C}{s} \right) \mathbb{P} \left(\left(\max_{k=1}^n |S_k|- s\right)_{+} \geq t \right) \leq \mathbb{P}(|S_n| \geq t). \end{align*} Integrating over $t$ from $0$ to $\infty$, we get $$ \mathbb{E} \left( \max_{k=1}^n |S_k|- s\right)_{+} \leq \left(1-\dfrac{2C}{s}\right)^{-1} \mathbb{E}|S_n| \leq \dfrac{Cs}{s-2C}.$$ Take $s=3C$ and conclude that $$ \mathbb{E}\left( \max_{k=1}^n |S_k| \right) \leq \mathbb{E} \left( \max_{k=1}^n |S_k|- 3C\right)_{+} + 3C \leq 6C.$$ Taking $n \uparrow \infty$, we conclude that $\mathbb{E}(\sup_{n \geq 1} |S_n|) < \infty$. Now $S_n$ is a MG with respect to its canonical filtration and $T$ is a stopping time. Apply OST to get that \mathbb{E}(S_{T \wedge n})=0$ for all $n$. Since $T<\infty$ almost surely, we have $S_{T \wedge n}$ converges to $S_T$ almost surely. Moreover, $$ \mathbb{E}\left( \max_{k\geq 1} |S_{T \wedge k}| \right) \leq \mathbb{E}\left( \max_{k\geq 1} |S_{k}| \right) < \infty,$$ and hence $\left\{S_{T \wedge n}, n \geq 1\right\}$ is uniformly integrable. Use \textit{Vitali's Theorem} to conclude that $\mathbb{E}(S_T)=0.$
|
s1-teasers: 논리 퍼즐 (Logical Puzzle)
📌 질문:
5명의 그룹이 비밀 문서를 금고에 보관하고자 한다.
앞으로 3명 이상이 모여야 금고를 열 수 있도록 하고 싶다.
따라서 금고에 여러 개의 자물쇠를 걸고, 각 자물쇠는 여러 개의 열쇠를 가질 수 있다.
단, 각 열쇠는 하나의 자물쇠만 열 수 있다.
최소 몇 개의 자물쇠가 필요할까?
📌 해설:
- 두 명의 조합(5명 중 2명)마다 금고를 열 수 없도록 해야 함.
- 5명 중 2명을 제외한 나머지 3명에게 해당 자물쇠의 열쇠를 부여.
- 5명 중 2명을 선택하는 모든 경우의 수는 10개
- 각 자물쇠는 해당 조합을 제외한 3명에게만 열쇠를 부여하므로,
- 각 자물쇠당 3개의 열쇠가 필요함.
- 5명 중 각자가 얻는 열쇠 개수는 6
✅ 결론: 최소 10개의 자물쇠가 필요함.
➡ 각 자물쇠는 특정 2명을 제외한 나머지 3명에게만 열쇠를 배분해야 하기 때문.
|
quesiton
|
solution
|
|
A group of 5 people want to keep their secret document in a safe. They want to make sure that in future, only a majority (>=3) can open the safe. So they want to put some locks on the safe, each of the locks have to be opened to access the safe. Each lock can have multiple keys; but each key only opens one lock. How many locks are required at the minimum?
|
For each group of 2 people, there must be a lock which none of them have a key to. But the key of such a lock will be given to the remaining 3 people of group. Each lock has 3 keys, which is given to unique 3-member subgroup. So each member should have 10 * 3 / 5
|
실제 데이터에는 Q&A로 되어있는데, 이걸 가지고 어떻게 Wait을 발생시키는 지는 좀 더 확인이 필요해보인다.
코드
서빙 코드
이 코드는 s1-32B 모델을 활용하여 Budget Forcing을 적용한 Test-time Scaling을 수행하는 방법을 구현한 것입니다.
논문에서 소개한 Budget Forcing 기법을 실제로 적용하여 모델의 reasoning 과정을 제어하는 방식입니다.
핵심 개념 정리
✅ vLLM 사용 → vllm.LLM을 활용하여 대형 언어 모델을 서빙
✅ Budget Forcing 적용 → Wait 토큰을 추가하여 모델의 사고 과정을 연장
✅ MAX_TOKENS_THINKING = 32000 → 모델이 추론할 수 있는 최대 토큰 수를 제한
✅ NUM_IGNORE = 1 → end-of-thinking 토큰을 무시하는 횟수 (즉, 한 번 더 깊이 사고하도록 유도)
이 코드는 논문의 Budget Forcing 기법을 그대로 적용한 예제입니다.
📌 논문과 코드의 핵심 개념 매칭
| 논문 내용 | 코드 구현 |
| Budget Forcing 기법 적용 | ignore_str = "Wait"을 추가하여 사고 과정 연장 |
| Test-time Scaling (Sequential Scaling) | NUM_IGNORE를 통해 사고 시간 조절 |
| 최대 사고 토큰 제한 (MAX_TOKENS_THINKING) | max_tokens_thinking_tmp = 32000으로 설정 |
| 최종 응답을 위한 Stop Token 사용 | `stop_token_ids = tok("< |
| Sequential Scaling이 Parallel보다 효과적임을 검증 | Majority Voting 없이 Wait을 활용한 사고 과정 적용 |
from vllm import LLM, SamplingParams
from transformers import AutoTokenizer
# Decide on a token limit for thinking; As the model's max tokens is 32768, 32000 usually ensures there is enough space for the model to still answer
MAX_TOKENS_THINKING = 32000
# Decide how often to ignore end-of-thinking token
NUM_IGNORE = 1
model = LLM(
"simplescaling/s1-32B",
tensor_parallel_size=2,
)
tok = AutoTokenizer.from_pretrained(
"simplescaling/s1-32B"
)
stop_token_ids = tok("<|im_end|>")["input_ids"]
sampling_params = SamplingParams(
max_tokens=32768,
min_tokens=0,
stop_token_ids=stop_token_ids,
skip_special_tokens=False,
temperature=0.0,
)
# For the exact raspberry sample in the paper, change
# model to `qfq/1k_qr_bt_dm_po_steps` (an earlier version of s1)
# & prompt to `How many r in raspberry?`
prompts = [
"How many r in raspberry",
]
for i, p in enumerate(prompts):
prompt = "<|im_start|>system\nYou are Qwen, created by Alibaba Cloud. You are a helpful assistant.<|im_end|>\n<|im_start|>user\n" + p + "<|im_end|>\n<|im_start|>assistant\n"
stop_token_ids = tok("<|im_start|><|im_end|>")["input_ids"]
sampling_params = SamplingParams(
max_tokens=MAX_TOKENS_THINKING,
min_tokens=0,
stop_token_ids=stop_token_ids,
skip_special_tokens=False,
temperature=0.0,
)
prompt += "<|im_start|>think"
o = model.generate(
prompt,
sampling_params=sampling_params
)
ignore_str = "Wait"
max_tokens_thinking_tmp = MAX_TOKENS_THINKING
# Num of times to skip stop token
for i in range(NUM_IGNORE):
max_tokens_thinking_tmp -= len(o[0].outputs[0].token_ids)
prompt += o[0].outputs[0].text + ignore_str
sampling_params = SamplingParams(
max_tokens=max_tokens_thinking_tmp,
min_tokens=1,
stop_token_ids=stop_token_ids,
skip_special_tokens=False,
temperature=0.0,
)
o = model.generate(
prompt,
sampling_params=sampling_params
)
### Final answer ###
prompt += o[0].outputs[0].text
stop_token_ids = tok("<|im_end|>")["input_ids"]
sampling_params = SamplingParams(
max_tokens=32768,
min_tokens=0,
stop_token_ids=stop_token_ids,
skip_special_tokens=False,
temperature=0.0,
)
o = model.generate(
prompt,
sampling_params=sampling_params,
)
print("With budget forcing:")
print(prompt + o[0].outputs[0].text)
참고
'관심있는 주제 > LLM' 카테고리의 다른 글
| MemOS: 대형 언어 모델을 위한 메모리 운영체제-논문 리뷰 및 정리 (5) | 2025.07.12 |
|---|---|
| 프롬프트 최적화 오픈소스 정리 (1) | 2025.05.07 |
| 논문 정리) DeepSeek (V3,R1) 논문을 보면서 기술적인 부분 알아보기 (2) | 2025.01.27 |
| LLM) HuggingFace 모델 다운로드부터 gguf 및 quantization 수행 후 vLLM 서빙하는 순서 정리해보기 (테스트 필요) (3) | 2024.11.16 |
| LangChain Products 알아보기 (LangChain, LangGraph, LangSmith, LangServe) (0) | 2024.08.07 |